В некоторых задачах приходится рассматривать не только вопрос о времени безотказной работы (т.е. времени появления первого отказа) элементов и систем, но и учитывать появление ряда отказов технических устройств за определенный период времени. Например, такие задачи могут возникнуть при рассмотрении организационных вопросов технического обслуживания технических устройств (организация ремонта, замены и т.д.) и при исследовании надежности резервированных систем. Иногда предполагается, что появления последовательных отказов можно считать редкими событиями, распределенными по закону Пуассона. При этом возможны два подхода к этому вопросу.
Если задать время работы системы, то при показательном распределении времени безотказной работы вероятность появления 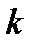 отказов за время
отказов за время 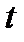 вычисляется по формуле Пуассона:
вычисляется по формуле Пуассона:
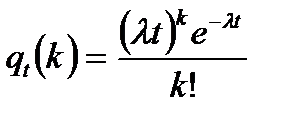 , (7.5)
, (7.5)
где 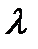 - интенсивность отказов (среднее число отказов в единицу времени в рассматриваемом интервале);
- интенсивность отказов (среднее число отказов в единицу времени в рассматриваемом интервале);
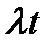 - параметр распределения.
- параметр распределения.
Вероятность появления не менее  отказов за фиксированный интервал
отказов за фиксированный интервал 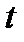 равна
равна
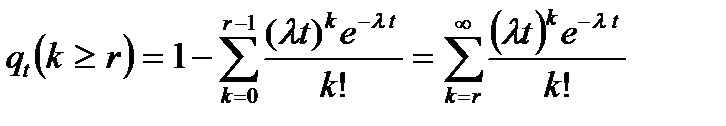 (7.6)
(7.6)
В теории надежности распределение Пуассона используется в задачах, связанных с расчетом необходимого числа запасных частей и других.
Если задать фиксированное число отказов 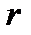 и рассматривать в качестве случайной переменной время до появления заданного числа
и рассматривать в качестве случайной переменной время до появления заданного числа 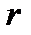 отказов, то плотность распределения этой случайной величины определяется распределением Эрланга:
отказов, то плотность распределения этой случайной величины определяется распределением Эрланга:
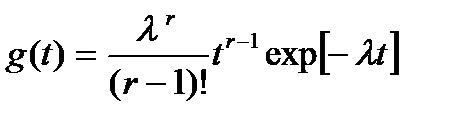 , (7.7)
, (7.7)
где 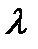 – параметр масштаба;
– параметр масштаба;  – параметр формы.
– параметр формы.
Функция распределения
 . (7.8)
. (7.8)
Распределение Эрланга используется для описания многофазных процессов, случайных времен работы невосстанавливаемой системы с холодным резервом.
При 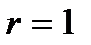 получается экспоненциальное распределение. В данном случае экспоненциальное распределение – это распределение времени ожидания первого отказа. Распределение Пуассона тесно связано с экспоненциальным распределением и распределением Эрланга. Пусть
получается экспоненциальное распределение. В данном случае экспоненциальное распределение – это распределение времени ожидания первого отказа. Распределение Пуассона тесно связано с экспоненциальным распределением и распределением Эрланга. Пусть  -моменты появления отказов.
-моменты появления отказов.  - случайные промежутки времени между этими отказами.
- случайные промежутки времени между этими отказами.  - число отказов в фиксированном интервале времени
- число отказов в фиксированном интервале времени  . Если случайные величины
. Если случайные величины 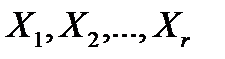 независимы и каждая из них распределена по экспоненциальному распределению с одним и тем же параметром масштаба
независимы и каждая из них распределена по экспоненциальному распределению с одним и тем же параметром масштаба  , то случайное число
, то случайное число 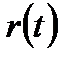 отказов в интервале фиксированной длины
отказов в интервале фиксированной длины 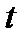 подчиняется закону Пуассона с параметром
подчиняется закону Пуассона с параметром  , а случайная величина
, а случайная величина 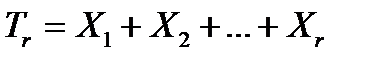 имеет распределение Эрланга порядка
имеет распределение Эрланга порядка  с параметром масштаба
с параметром масштаба 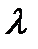 . При этом имеет место равенство
. При этом имеет место равенство
 . (7.9)
. (7.9)
В распределении Эрланга параметр формы 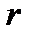 является целым положительным числом. Если параметр формы будет положительным числом, то это распределение переходит в гамма-распределение. Плотность гамма-распределения имеет вид
является целым положительным числом. Если параметр формы будет положительным числом, то это распределение переходит в гамма-распределение. Плотность гамма-распределения имеет вид
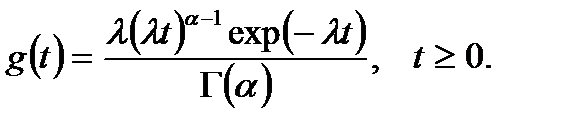 (7.10)
(7.10)
где  – параметр формы,
– параметр формы, 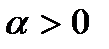 ;
;  – параметр масштаба,
– параметр масштаба,  .
.
Числовые характеристики:
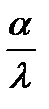 – математическое ожидание;
– математическое ожидание;
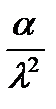 – дисперсия;
– дисперсия;
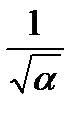 – коэффициент вариации;
– коэффициент вариации;
 – коэффициент асимметрии;
– коэффициент асимметрии;
 – коэффициент эксцесса;
– коэффициент эксцесса;
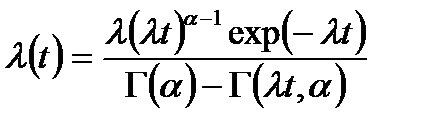 – интенсивность отказов;
– интенсивность отказов;
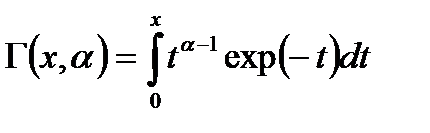 – неполная гамма-функция.
– неполная гамма-функция.
При целых значениях 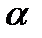 функция распределения имеет вид
функция распределения имеет вид
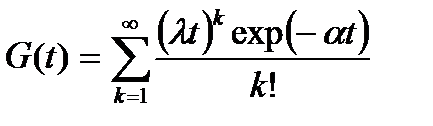 . (7.11)
. (7.11)
При  будем иметь экспоненциальное распределение.
будем иметь экспоненциальное распределение.
На рис. 7.4 представлены графики плотности гамма-распределения.
Рис. 7.4. График плотности гамма-распределения
На рис. 7.5 показа кривая интенсивности отказов
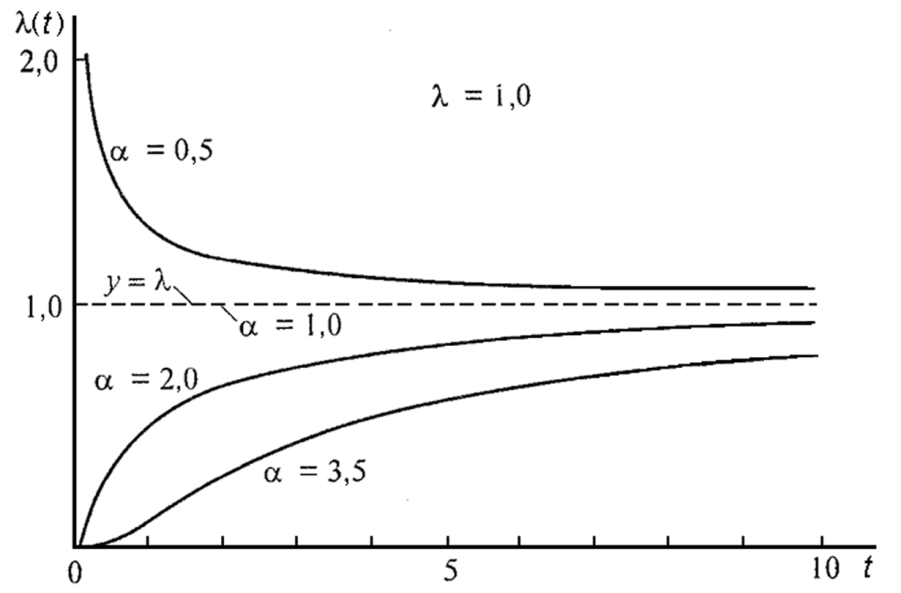
Рис. 7.5. График интенсивности отказов гамма-распределения
Гамма– распределение возникает в теории нормально распределённых величин как распределение суммы квадратов независимых величин, имеющих стандартное нормальное распределение. Оно находит применение в экологии, а также при анализе периода полураспада. Гамма-распределения используют для описания резервированной системы, состоящей из одинаковых блоков, причем под нагрузкой находится один блок, а остальные поочередно автоматически включаются в работу после отказа работающего блока. Это распределение применяется в тех же случаях, что и Вейбулла-Гнеденко, а кроме этих случаев для описания накапливающихся повреждений (изгибающие нагрузки слоистых брусков, систем с ненагруженным резервом и т.п.).
Распределение смеси
Чтобы получить теоретическое распределение, близкое к экспериментальному, иногда применяют следующий прием. Плотность распределения времени безотказной работы считается равной сумме (суперпозиция):
 , (7.12)
, (7.12)
где 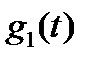 ,
,  - теоретические распределения определенного вида;
- теоретические распределения определенного вида;
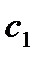 ,
, 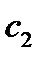 - коэффициенты веса, учитывающие влияние различных слагаемых.
- коэффициенты веса, учитывающие влияние различных слагаемых.
Рассмотрим в качестве примера сумму (суперпозицию) распределений:
 . (7.13)
. (7.13)
Для этого случая имеем:
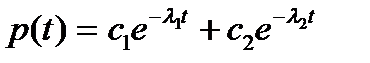 , (7.14)
, (7.14)
 . (7.15)
. (7.15)
Соответствующий график распределения  приведен на рис. 7.6.
приведен на рис. 7.6.
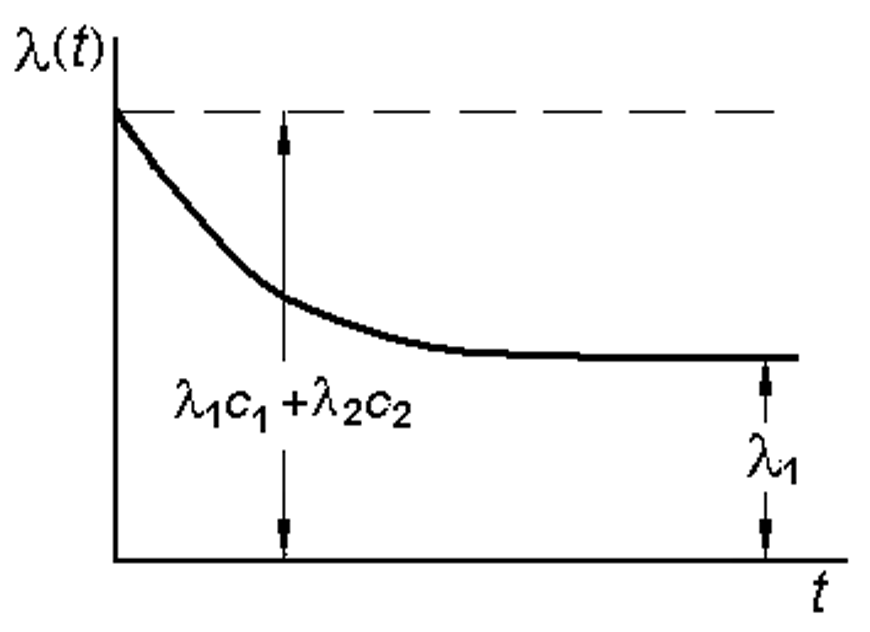
Рис. 7.6. График  для суммы (суперпозиции) двух показательных распределений
для суммы (суперпозиции) двух показательных распределений
Среднее время безотказной работы:
 . (7.16)
. (7.16)
Пусть для определенности  . Тогда для очень больших
. Тогда для очень больших  (
(  ) члены, содержащие
) члены, содержащие  , малы и
, малы и 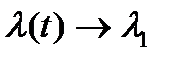 . При малых значениях
. При малых значениях 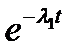 и
и  близки к единице и
близки к единице и
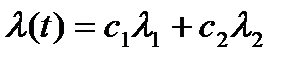 . (7.17)
. (7.17)
Дата: 2018-11-18, просмотров: 988.