Экспоненциальное (показательное) распределение является следствием предположения о том, что относительная скорость уменьшения вероятности безотказной работы с увеличением заданного времени работы является величиной постоянной:

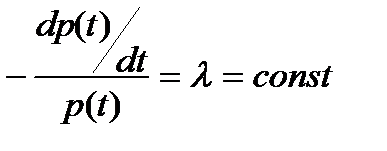                                                                                                          (6.1)

Случайная величина Т имеет экспоненциальное распределение, если её плотность распределения имеет вид:

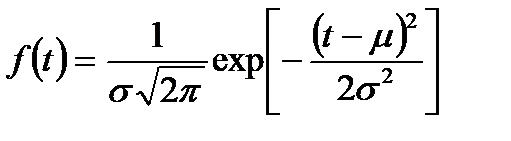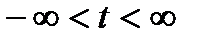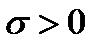                  , , .                                 (6.2)

Функция экспоненциального распределения будет равна:

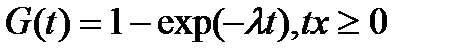                                       .                                                       (6.3)

Плотность распределения:

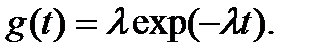                                                                                                                 (6.4)

Числовые характеристики:

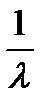 – математическое ожидание;

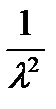– дисперсия;

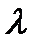
– интенсивность отказов;

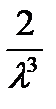–третий центральный момент;

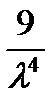 – четвертый центральный момент.

На рис. 6.3 приведен график плотности экспоненциального распределения.

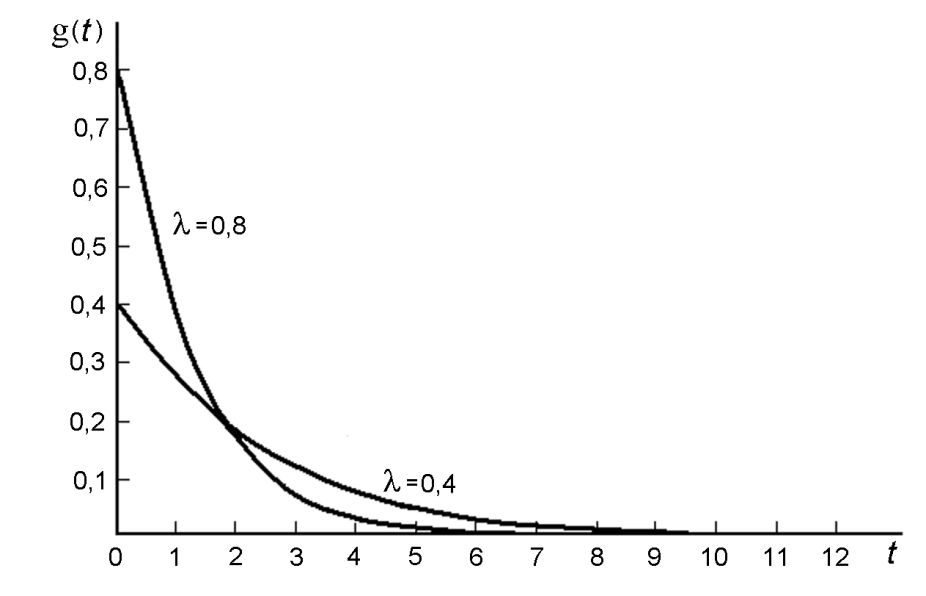
Рис. 6.3. График плотности экспоненциального распределения.

На рис.6.4 приведен график интенсивности отказов

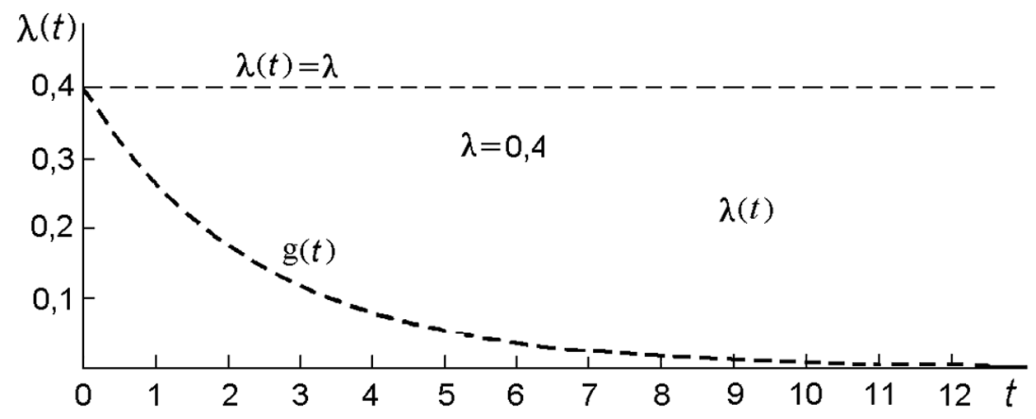
Рис. 6.4. График интенсивности отказов экспоненциального распределения.

При экспоненциальном распределении наработки до отказа минимальная наработка до отказа 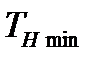 определится соотношением

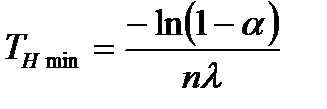                                          ,                                                            (6.5)

где 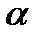 – риск изготовителя, равный вероятности получения отрицательного результата испытаний на долговечность;

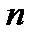– объем выборки для испытаний на долговечность.

Средняя наработка

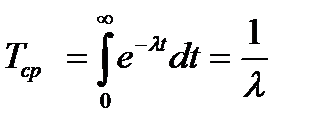                                                  .                                                         (6.6)

Функция надежности при 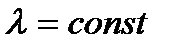 может быть записана в виде

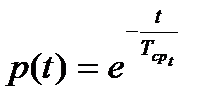                                                          .                                                           (6.7)

Среднее время безотказной работы элемента или системы при 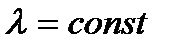 можно понимать как время работы 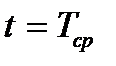, в течение которого элемент или система остается работоспособной с вероятностью .

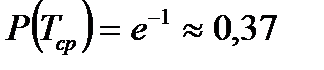Для экспоненциального распределения наработки до отказа 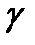 –процентный ресурс определится выражением

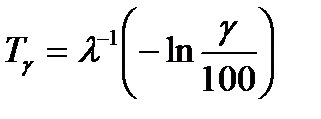                                                   .                                                       (6.8)

Характерным признаком экспоненциального распределения является равенство коэффициента вариации единице.

Экспоненциальное распределение используется для описания процесса появления редких событий, повторяющихся «случайно во времени»: процессы восстановления систем, состоящих из большого числа элементов, эксплуатации систем на периоде , где интенсивности отказов её элементов близки к постоянной величине, и др. Таким образом, если объект не отказал к рассматриваемому моменту времени, то вероятность его отказа а последующую единицу времени будет та же, что и в начальный момент эксплуатации. Если время безотказной работы описывается экспоненциальным распределением, то система обладает свойством отсутствия последействия, которое означает, что условная вероятность 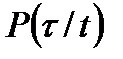 безотказной работы в течение интервала  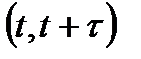при условии, что до момента  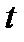отказов не было, зависит только от длины интервала:

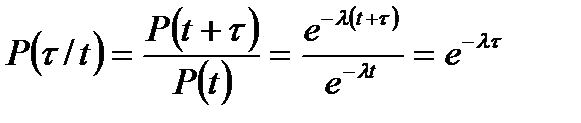                                       .                                           (6.9)

Физика этого события состоит в отсутствии старения элементов.

Показательный закон распределения применяется чаще других при исследовании надежности элементов и систем. Это объясняется рядом причин.

Во-первых, показательное распределение времени безотказной работы типично для сложных систем, состоящих их разнородных элементов с различными 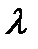-характеристиками. Интенсивность отказов сложной системы, состоящей из многих элементов с различными 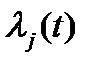, может быть постоянной и при существенно нестационарных интенсивностях отказов отдельных элементов. Кроме того, при исследовании надежности отдельных элементов иногда можно пренебречь повышенной интенсивностью отказов в начальный период эксплуатации или устранить этот период применением приработки (тренировки). Если в процессе эксплуатации этих элементов не наступает период износа, то интенсивность отказов в этом случае можно считать постоянной.

Во-вторых, при стационарных интенсивностях отказов элементов получаются очень простые формулы для расчета надежности элементов и систем. Если учесть, что сложные системы иногда состоят из сотен тысяч элементов, то становится очевидной важность упрощения расчета надежности. При 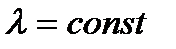 вероятность безотказной работы элемента или системы в течение заданного периода времени  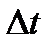не зависит от «возраста» объекта, т.е. от положения периода времени  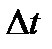на оси времени эксплуатации. Это существенно упрощает расчеты.

В-третьих, исследования надежности очень часто поводятся при наличии малой информации об отказах аппаратуры в процессе ее эксплуатации или испытаний. При ограниченных экспериментальных данных очень трудно обнаружить «значительные отклонения» от гипотезы 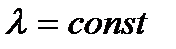, даже если имеется возможная нестационарность 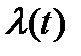. Если экспериментальных данных недостаточно, чтобы выявить истинный характер нестационарности 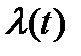, то вполне естественно в качестве первого приближения принять вид теоретического распределения, удобный для вычислений и чаще других встречающийся на практике, т.е. показательное распределение.

Показательное распределение времени безотказной работы является довольно грубым приближением к действительности и его целесообразно использовать лишь в тех случаях, когда можно пренебречь влиянием износа. Допущение о том, что интенсивность отказов постоянна, аналогична предположению о неизменяемости физико-химических свойств материалов. В действительности все технические устройства изнашиваются и стареют.

Модель экспоненциального распределения часто используется для априорного анализа, так как позволяет получить простые соотношения для различных вариантов создаваемой системы. На стадии апостериорного анализа (опытных данных) должна проводиться проверка соответствия экспоненциальной модели результатам испытаний.

Нормальное распределение

При нормальном (гауссовском) распределении случайной величины она может принимать любые значения от 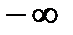 до .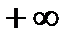

К распределениям этого типа относятся :

 – гауссовское распределение;

 – гауссовское (усеченное слева);

 – логарифмически нормальное;

 – обратное гауссовское.

Так как для этого распределения 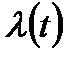 – возрастающая функция времени, то при выполнении условия закона больших чисел распределение гауссовского типа пригодны для описания поведения стареющих систем.

Случайная величина Т называется нормально распределённой, если её плотность распределения имеет вид:

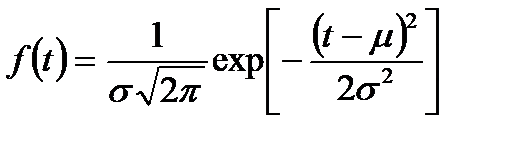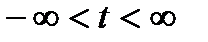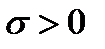                   , , .                              (6.10)

Функция распределения:

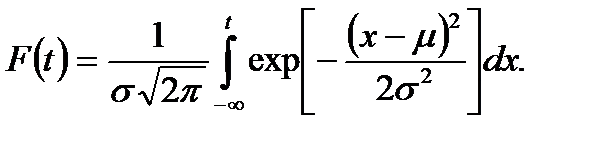                                                                                   (6.11)

Плотность распределения случайной величины 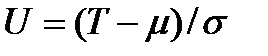 равна

.

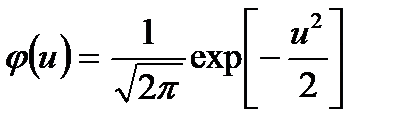Эта плотность отвечает стандартному нормальному распределению, а случайная величина 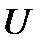 – называется стандартной нормальной величиной.

В различных приложениях используется функция распределения 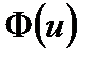 –– интеграл вероятности

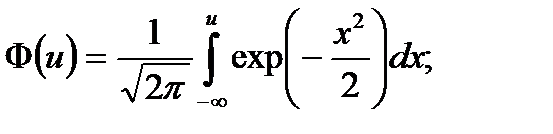                                                                                        (6.12)

В этом случае квантили распределения определяются так

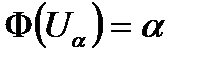                                                      ,                                                              (6.13)

где 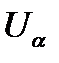 – нижняя 100 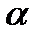%-я квантиль стандартного нормального распределения, а  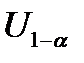– верхняя 100 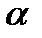%-я квантиль.

Параметр  иногда заменяется коэффициентом точности

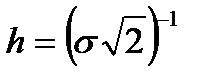                                                     .                                                          (6.14)

Используются и другие функции, связанные с нормальным распределением

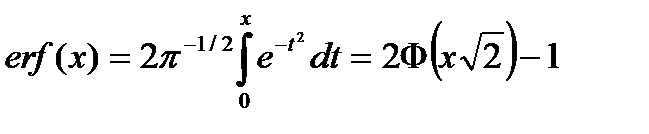                                     ,                                    (6.15)

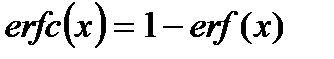                                                   .                                                    (6.16)

Здесь 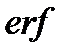 – функция ошибок или интеграл ошибок,  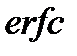– дополнение до единицы функции ошибок.

В приложениях используется следующее выражение

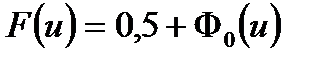                                                  ,                                                      (6.17)

где 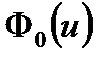 – функция Лапласа

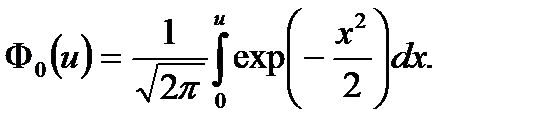                                                                                         (6.18)

Числовые характеристики:

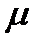 – математическое ожидание;

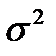 – дисперсия;

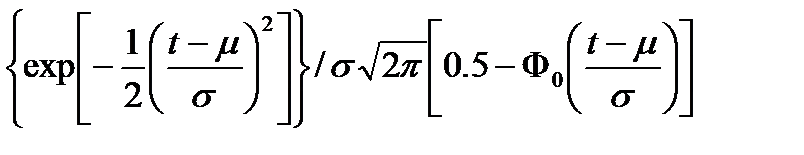 – интенсивность отказов;

Относительную меру разброса случайной величины характеризует коэффициент вариации .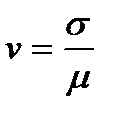

Коэффициент асимметрии равен нулю.

На рис. 6.5 приведён график плотности нормального распределения.

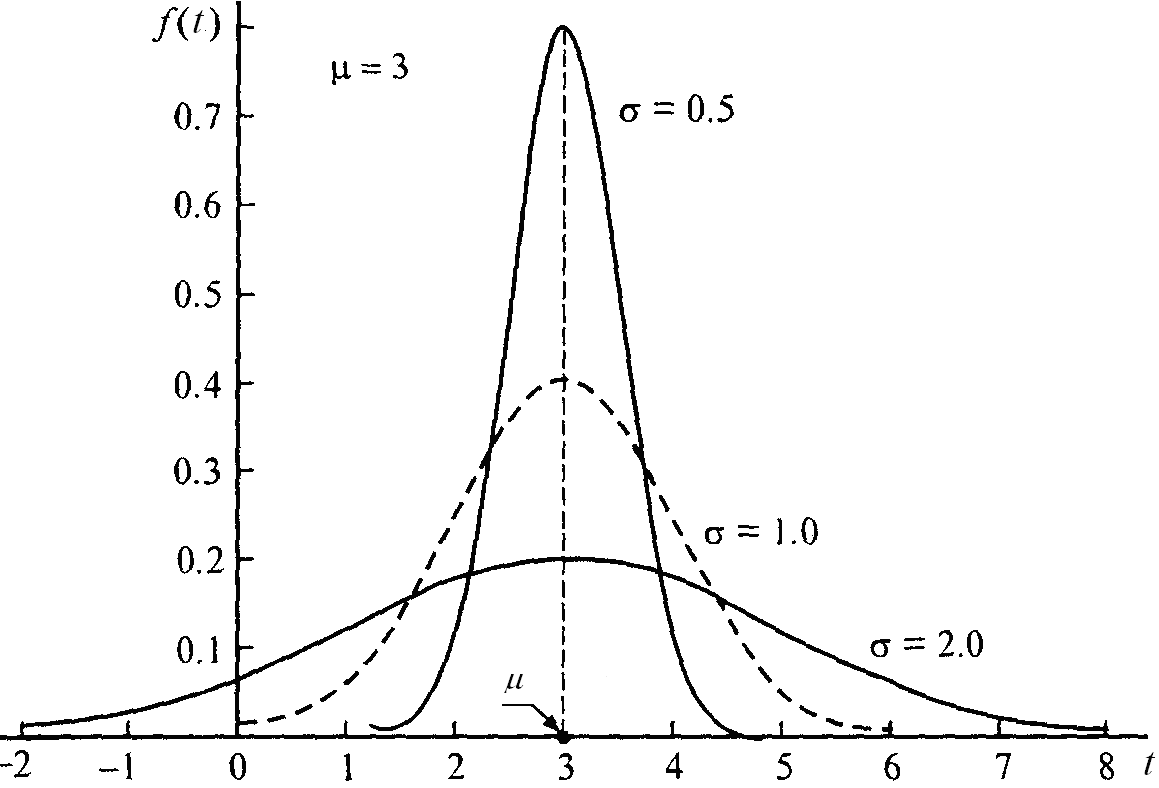
Рис.6.5. График плотности нормального распределения

На рис. 6.6 приведен график интенсивности отказов.

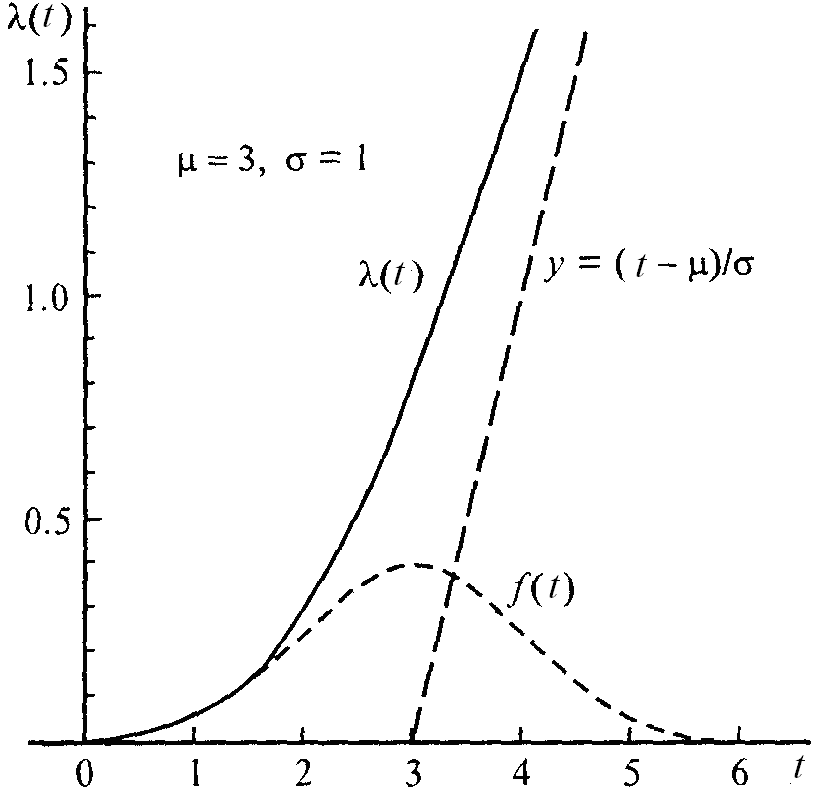
Рис. 6.6. График интенсивности отказов нормального распределения

В соответствии с центральной предельной теоремой функция распределения случайной величины, являющейся суммой одинаково распределённых независимых случайных величин, приближается к функции нормального распределения с ростом числа слагаемых. Важным свойством нормального распределения является то, что нормальная случайная величина с большой вероятностью принимает значения, близкие к своему математическому ожиданию. Это свойство выражается правилом трех сигм:

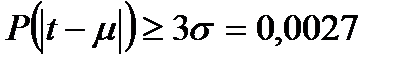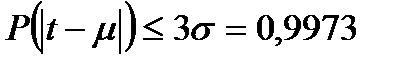              ,         .                            (6.19)

Нормальное распределение времени безотказной работы наблюдается у изготовленных при устойчивом ходе производства сравнительно простых механических устройств с однородными характеристиками разрушения. Необходимо отметить, что вопреки распространенному мнению при отказах элементов технических устройств за счет износа распределение времени безотказной работы будет далеко не всегда нормальным. Необходимым условием нормального распределения времен безотказной работы является малый разброс значений скорости износа элементов. Ввиду большого теоретического и прикладного значения нормального распределения его стараются иногда применить и при явно несимметричных распределениях времени безотказной работы. Для этого подбирают некоторую функцию случайного времени безотказной работы. Например 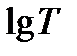,  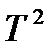и т.д., приближенно следующую нормальному закону. Например, довольно часто используется логарифмически нормальное распределение усталостной долговечности, при котором предполагается, что логарифм числа циклов нагрузки распределен по нормальному закону.

Поскольку возможные значения случайного времени безотказной работы 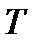 могут быть только положительными, распределение  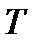может быть лишь усеченным нормальным.