Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Работоспособность системы в момент времени  определяется состоянием отдельных её элементов в этот момент. При этом простыми событиями являются безотказная работа или отказ отдельных элементов, а сложное событие – безотказная работа системы. Взаимосвязь простых событий и сложного события можно описать с помощью структурной схемы надежности. Элементы системы могут быть соединены между собой различным образом. Соединения представляют собой структуры, а сами структуры носят название структурных схем надежности, т.е. структурная схема – условный вид соединений элементов. Соединение элементов в структурных схемах надежности можно свести к четырем видам:

– последовательному;

– параллельному;

– смешанному;

– произвольному.

При расчете надежности структурных схем надежности в качестве основных показателей надежности используются вероятность безотказной работы и вероятность отказа.

Последовательное соединение элементов – соединение, при котором отказ хотя бы одного элемента приводит к отказу всей системы. Структурная схема надежности системы, состоящей из  независимых последовательно соединенных элементов, представлена на рис.8.1.

1

2

3

 

 

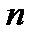
Рис. 8.1. Структурная схема надежности системы с последовательным соединением элементов

 

Такое соединение элементов в технике встречается наиболее часто, поэтому его называют основным соединением. В системе с последовательным соединением для безотказной работы в течение некоторой наработки необходимо и достаточно, чтобы каждый из ее элементов работал безотказно в течение этой наработки. Считая отказы элементов независимыми, вероятность одновременной безотказной работы 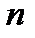 элементов за заданное время  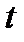определяется по теореме умножения вероятностей: вероятность совместного появления независимых событий равна произведению вероятностей этих событий. Тогда вероятность безотказной работы системы  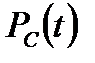за заданное время  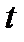равна

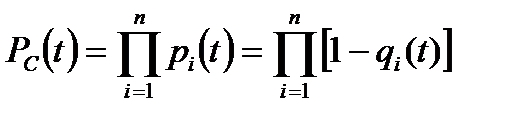                                 ,                                                      (8.9)

где 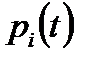 – вероятность безотказной работы  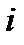– го элемента;  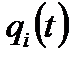– вероятность отказа  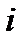– го элемента.

При значениях вероятности безотказной работы элементов, близких к единице можно использовать приближенную формулу

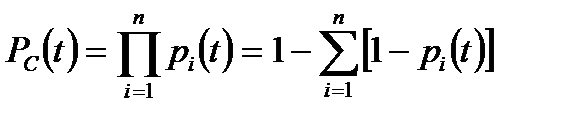                                  .                                               (8.10)

Вероятность отказа системы 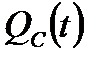будет равна

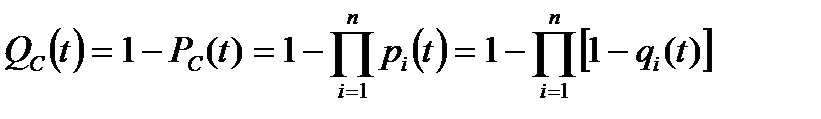                          .                               (8.11)

Если система состоит из равнонадёжных элементов ( 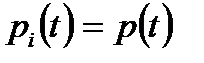), то

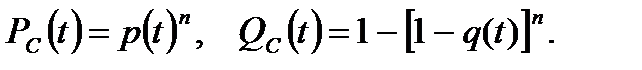                                                                    (8.12)

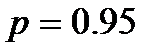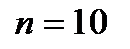Из формул (8.10) и (8.11) очевидно, что даже при высокой надежности элементов надежность системы при последовательном соединении оказывается тем более низкой, чем больше число элементов (например, при  и   имеем 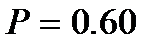, при , а при 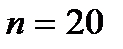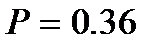). Кроме того, поскольку все сомножители в правой части выражения (8.10) не превышают единицы, вероятность безотказной работы системы при последовательном соединении не может быть выше вероятности безотказной работы самого ненадежного из ее элементов ( .) и из малонадежных элементов нельзя создать высоконадежной системы с последовательным соединением.

Если наработки элементов и системы подчиняются экспоненциальному распределению то можно записать

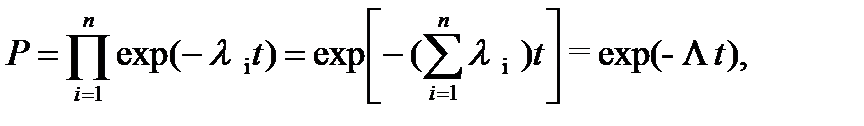                                         (8.13)

где

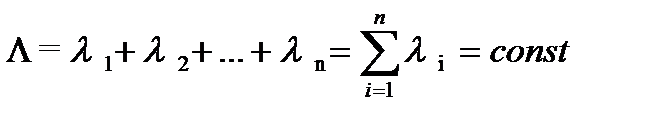- есть интенсивность отказов системы.

Таким образом, интенсивность отказов системы при последовательном соединении элементов равна сумме интенсивностей отказов элементов и для системы из 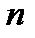 равнонадёжных элементов ( )

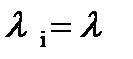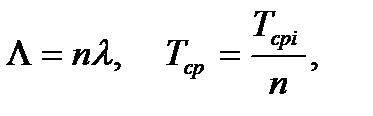                                                                                               (8.14)

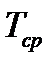т.е. интенсивность отказов в  раз больше, а средняя наработка до отказа системы  в 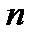 раз меньше, чем у отдельного элемента.

Точечная оценка вероятности безотказной работы системы с последовательным соединением элементов

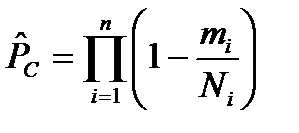                                             ,                                                               (8.15)

где 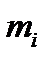 – число отказов  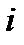го элемента;

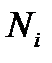 – объём испытаний.

Нижняя доверительная граница 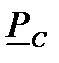вероятности безотказной работы системы с последовательным соединением элементов в интервале  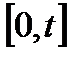при доверительной вероятности  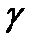по результатам испытаний вычисляется по приближенной зависимости

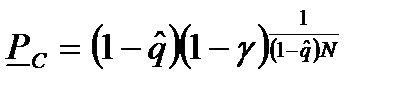                                       ,                                                      (8.16)

где  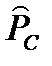– точечная оценка вероятности безотказной работы системы; 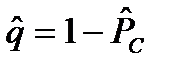, 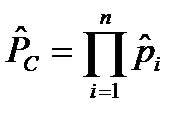;  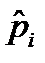– точечная оценка вероятности безотказной работы  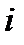– го элемента;  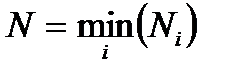– минимальный объем испытаний из  элементов.

Параллельное соединение элементов – соединение, при котором отказ системы происходит тогда и только тогда, когда откажут все элементы. Структурная схема надежности системы, состоящей из 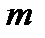 параллельно соединенных элементов, представлена на рис 8.2.

Рис.8.2. Структурная схема надежности системы с параллельным соединением элементов

Такие схемы надежности характерны для систем, в которых элементы дублируются или резервируются, т.е. параллельное соединение используется как метод повышения надежности. Однако такие системы встречаются и самостоятельно (например, системы двигателей четырехмоторного самолета или параллельное включение диодов в выпрямителях).

Для отказа системы с параллельным соединением элементов в течение наработки необходимо и достаточно, чтобы все ее элементы отказали в течение этой наработки. Так что отказ системы заключается в совместном отказе всех элементов, вероятность чего (при допущении независимости отказов) может быть найдена по теореме умножения вероятностей как произведение вероятностей отказа элементов. Таким образом, в случае системы, состоящей из 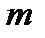 параллельно соединенных элементов (рис 8.2) вероятность безотказной работы системы  будет равна

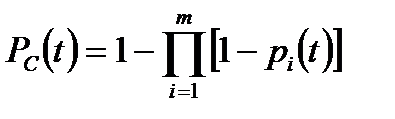                                            .                                         (8.17)

Вероятность отказа системы равна

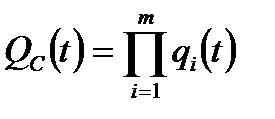                                                  .                                               (8.18)

В случае одинаковых значений вероятности отказа элементов  вероятность отказа системы будет равна

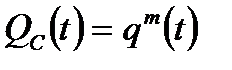                                                    .                                                 (8.19)

Таким образом, надежность системы с параллельным соединением повышается при увеличении числа элементов (например, пр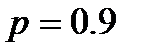и  и 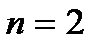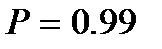, а если , то ).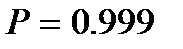

Поскольку 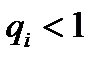, произведение в правой части (8.18) всегда меньше любого из сомножителей, т.е. вероятность отказа системы не может быть выше вероятности самого надежного ее элемента (“лучше лучшего”) и даже из сравнительно ненадежных элементов возможно построение вполне надежной системы.

При экспоненциальном распределении наработки элемента выражение (8.17) принимает вид

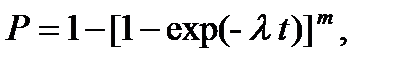                                                                                                 (8.20)

откуда с помощью после интегрирования и преобразований средняя наработка системы определяется

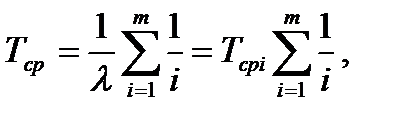                                                                                               (8.21)

где 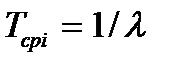 – средняя наработка элемента. При больших значениях  справедлива приближенная формула

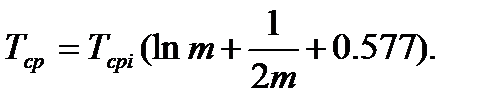                                                                                     (8.22)

Таким образом, средняя наработка системы с параллельным соединением больше средней наработки ее элементов (например, при 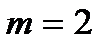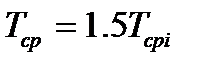, а если 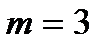, то ).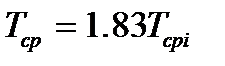

Если известна вероятность отказа элемента 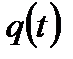, то для того, чтобы вероятность отказа системы не превосходила требуемой величины , необходимое число элементов определится выражением

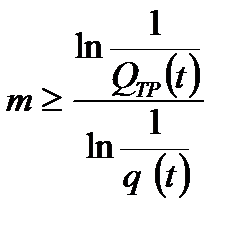                                                     .                                                           (8.23)

Нижняя доверительная граница вероятности безотказной работы системы с параллельным соединением элементов при доверительной вероятности  по результатам испытаний вычисляется по приближенной зависимости

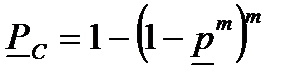                                                  .                                                        (8.24)

где 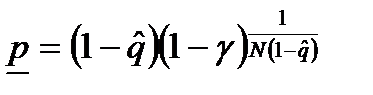; 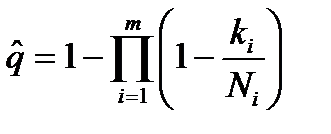, 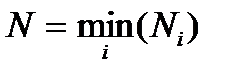;  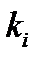– число отказов  – го элемента.

Cмешанное соединение элементов- соединение элементов, при котором структурные схемы надежности содержат как последовательные, так и параллельные структуры. В этом случае для расчета надежности структурную схему разбивают на последовательные или параллельные участки таким образом, чтобы каждый участок имел либо только последовательную, либо только параллельную структурную схему. На каждом участке определяется вероятность безотказной работы в соответствии с теми формулами, которые соответствуют структурным схемам рассматриваемого участка. Таким образом, исходная структурная схема надежности превращается в структуру с последовательным или параллельным соединением элементов.

Например, для структурной схемы надежности на рис. 8.3 эквивалентная последовательная структура имеет вид, представленный на рис 8.4.

 

 

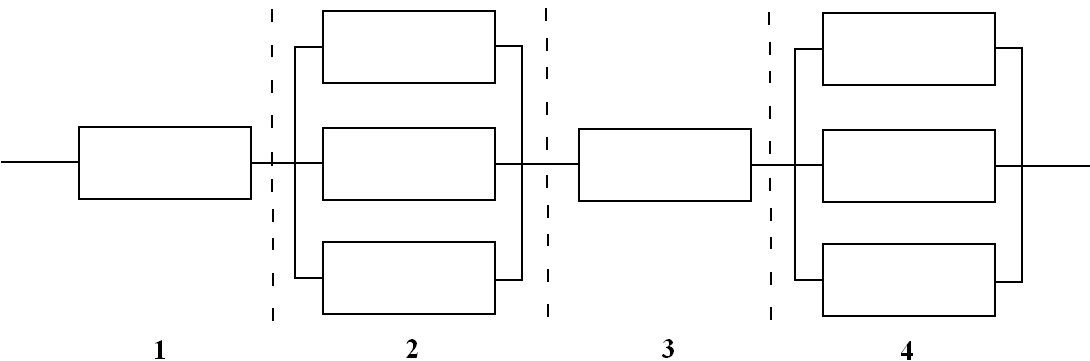
Рис. 8.3. Структурная схема надежности со смешанным соединением элементов

 

 

Рис. 8.4. Преобразованная структура со смешанным соединением элементов

Здесь 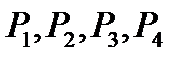 – вероятности безотказной работы соответственно первого, второго, третьего и четвертого последовательных участков, на которые структурная схема со смешанным соединением элементов предварительно была разбита. Тогда вероятность безотказной работы системы будет равна

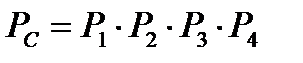                                             .                                             (8.25)

Если смешанное соединение элементов системы представляет собой последовательное соединение блоков, состоящих из параллельно соединенных элементов, то вероятность безотказной работы будет равна

                                        ,                                                       (8.26)

где 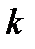-число блоков;  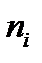– число элементов в -м блоке; 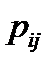 – вероятность безотказной работы 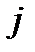-го элемента в  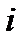-м блоке.

Когда невозможно при составлении структурных схем надежности применить последовательную, параллельную или смешанную схемы, то приходится иметь дело с так называемой сложной произвольной структурой.

Сложная произвольная структура – структура при составлении структурной схемы надежности невозможно применить последовательную или параллельную или смешанную схемы. Для систем с такими структурами в случае монотонности структуры широкое распространение получили методы расчета надежности:

– прямого перебора;

– путей и сечений;

Системы называются системой с монотонной структурой, если отказ любого элемента может привести только к ухудшению безотказности или отказу всей системы.

Рассмотрим метод перебора.

Пусть невосстанавливаемая система состоит из элементов и имеет произвольную структуру. Предположим, что отказы элементов события независимые. При допущении о нахождении каждого элемента только в двух возможных состояний (работоспособном и неработоспособном) число системы возможных состояний системы равно . Далее выделяются только те состояния, при нахождении в которых система считается работоспособной. Вероятность безотказной работы системы находится суммой вероятностей безотказной работы работоспособных состояний. Достоинством этого метода является использование последовательного рассмотрения каждого состояния и простота вычисления вероятности безотказной работы системы. Недостаток этого метода – расчеты становятся громоздкими при большом числе состояний.

В качестве примера рассмотрим мостиковую схему (рис.8.5).

Мостиковая схема не сводится к параллельному или последовательному типу соединения элементов, а представляет собой параллельное соединение последовательных цепочек элементов с диагональными элементами, включенными между узлами различных параллельных ветвей. Работоспособность такой системы определяется не только количеством отказавших элементов, но и их положением в структурной схеме.

 

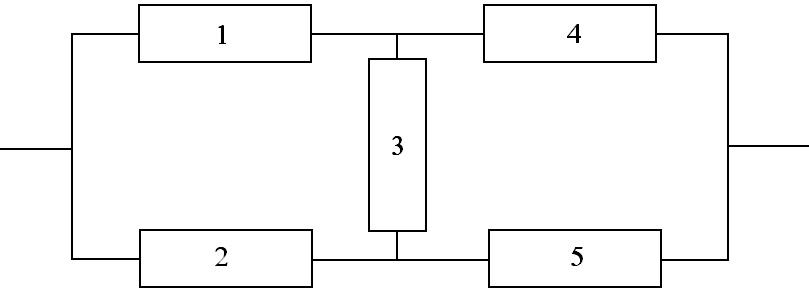
Рис. 8.5. Произвольная структурная мостиковая схема

 

Эта схема считается работоспособной при пяти вариантах отказов по одному элементу (отказавшие элементы: 1, или 2, или 3, или 4, или 5), при восьми вариантах отказов по два элемента (отказавшие группы элементов: 1 и 4, или 2 и 5, или 1 и 3, или 2 и 3, или 3 и 4, или 3 и 5, или 1 и 5, или 2 и 4), при двух вариантах отказа по трем элементам (отказавшие группы элементов: 1 и 3 и 4, или 2 и 3 и 5) или когда все 5 элементов работоспособны. Тогда, для случая равнонадежных элементов вероятность безотказной работы системы, структурная схема надежности которой представляет собой мостиковую схему, будет равна

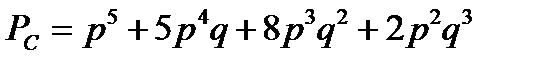                                        ,                                           (8.27)

где 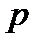 – вероятность безотказной работы одного элемента;  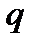– вероятность отказа одного элемента.

Если все элементы мостиковой системы равнонадежны и вероятность безотказной работы элемента 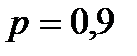, то .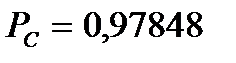

Для систем, содержащих статистически независимые элементы, структура которых не является последовательно-параллельной можно определять верхнюю и нижнюю оценки вероятности безотказной работы методом минимальных путей и сечений. Суть данного метода состоит в том, что структурная схема надежности представляется в виде двух эквивалентных схем:

–последовательного соединения минимальных сечений;

– параллельного соединения минимальных путей.

В этом случае вероятность безотказной работы системы оценивается «снизу» вероятностью безотказной работы эквивалентной последовательно-параллельной системы, представленной в виде последовательного соединения минимальных сечений – . Оценка «сверху» определяется вероятностью безотказной работы эквивалентной последовательно-параллельной системы, представленной в виде параллельного соединения минимальных путей- .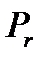

Минимальный путь – такой набор элементов в структуре, при котором система исправна, если исправны все элементы этого набора; отказ любого из элементов ведет к отказу системы.

Минимальное сечение – такой набор элементов в структуре, при котором система неисправна, если неисправны все элементы этого набора; исключение любого элемента из набора переводит систему в исправное состояние. У систем с произвольной структурой может быть несколько минимальных путей и минимальных сечений. Последовательное соединение из 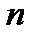  элементов имеют один минимальный путь и 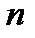минимальных сечений, проходящих через каждый элемент. Параллельное соединение из 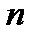элементов имеет  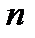минимальных путей, проходящих через каждый элемент, и одно минимальное сечение.

Таким образом, вероятность системы определяется неравенством

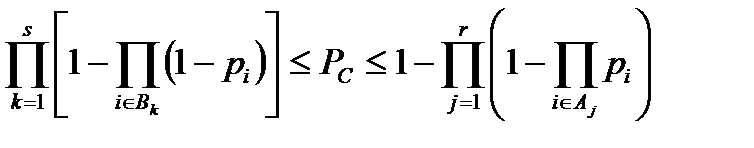                     ,                                          (8.28)

где 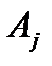- минимальные пути; 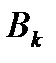- минимальные сечения.

Для схемы на рис. 8.5 минимальные пути и соответствующие им вероятности равны

      A1:1-4, ;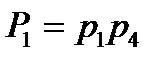

A2:2-5, ;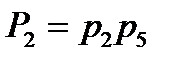

A3:1-3-5, ;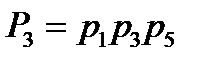

A4:2-3-4, 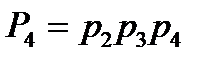.                                                                                                       (8.29)

Минимальные сечения и соответствующие им вероятности имеют вид

B1 : 1-2, ;

B2 :4-5, ;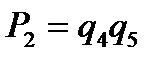

B3 :1-3-5, ;

B4 :2-3-4, 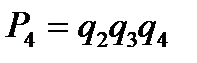.                                                                                                        (8.30)

Тогда вероятность безотказной работы системы определится неравенством

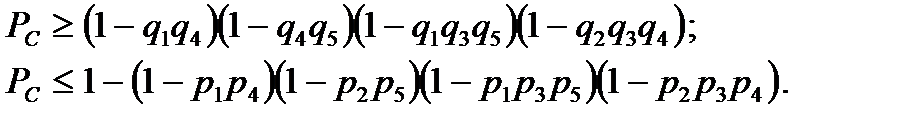                                                      (8.32)

Если все элементы мостиковой системы равнонадежны и вероятность безотказной работы элемента 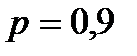, то

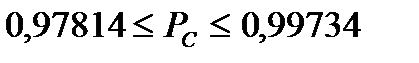                                          .                                                     (8.33)

Большинство реальных систем имеет сложную комбинированную структуру, часть элементов которой образует последовательное соединение, другая часть – - параллельное, отдельные ветви элементы или ветви структуры образуют мостиковые схемы или типа “ 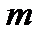 из 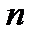”. Метод прямого перебора для таких систем практически не реализуем. Более целесообразно в этих случаях предварительно произвести декомпозицию системы, разбив ее на простые подсистемы – группы элементов, методика расчета надежности которых известна. Затем эти подсистемы в структурной схеме надежности заменяются квазиэлементами с вероятностями безотказной работы, равными вычисленным вероятностям безотказной работы этих подсистем. При необходимости такую процедуру можно выполнить несколько раз, до тех пор, пока оставшиеся квазиэлементы не образуют структуру, методика расчета надежности которой также известна.