Функция плотности логарифмически нормального распределения имеет вид:

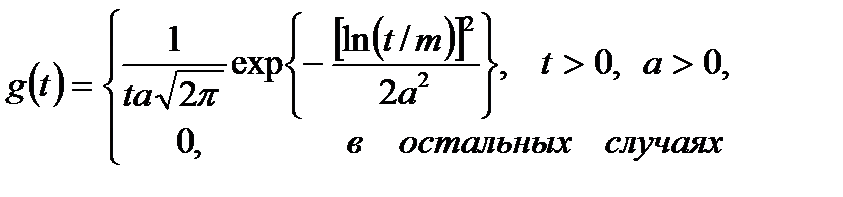       .                                             (6.23)

Здесь 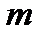 – параметр масштаба,  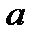– параметр формы.

Числовые характеристики:

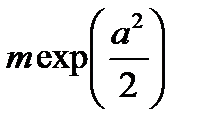 – математическое ожидание;

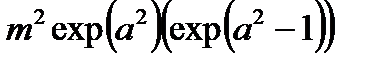 – дисперсия;

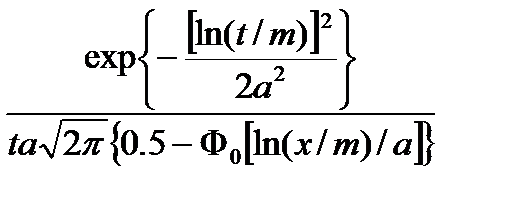 – интенсивность отказов;

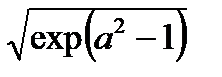- коэффициент вариации.

На рис 6.9 показан график плотности распределения.

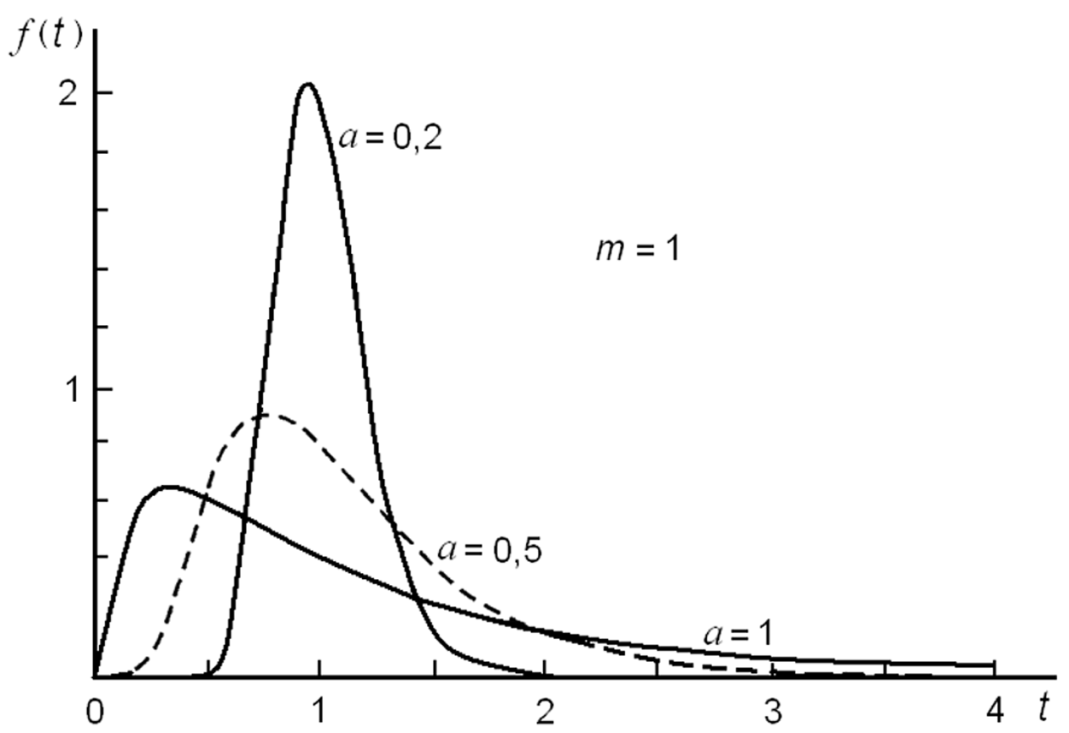
Рис. 6.9. График плотности логарифмически нормального распределения.

На рис 6.10 показан график интенсивности отказов

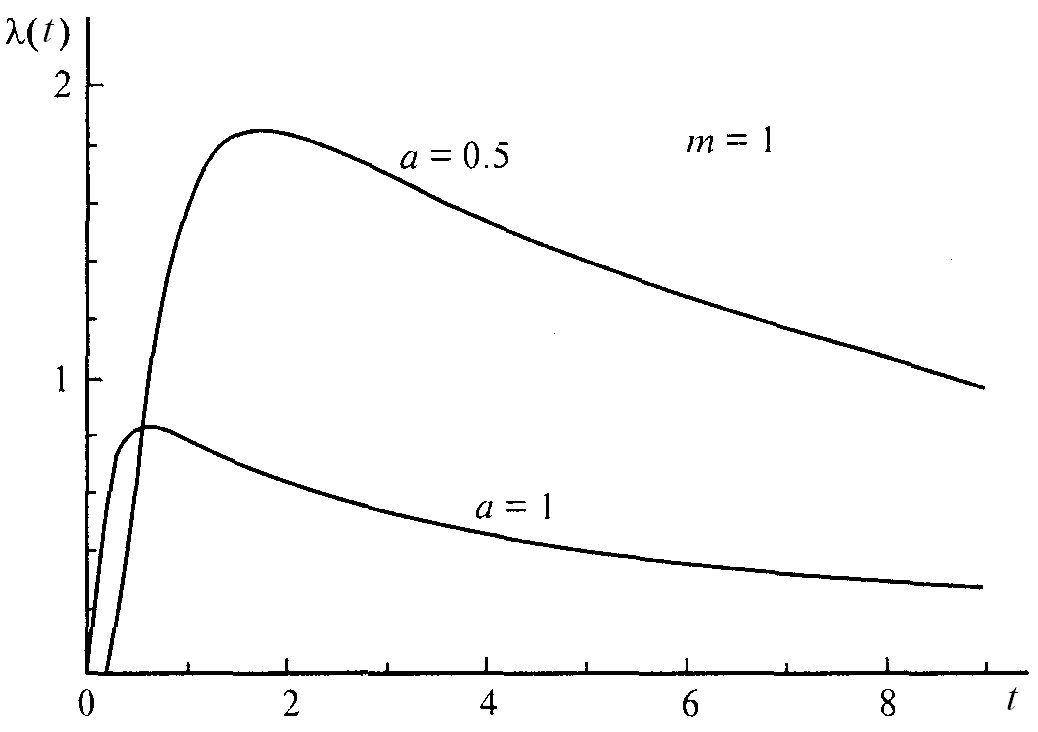
Рис. 6.10. График интенсивности отказов логарифмически нормального распределения

Логарифмически нормальное распределение величины 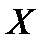 возникает в том случае, если величина  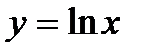имеет гауссовское распределение. Такая ситуация возникает, если во времени свойства объектов «упрочняются», что сопровождаются уменьшением скорости износа.

6.6. Обратное гауссовское распределение          

Плотность распределения

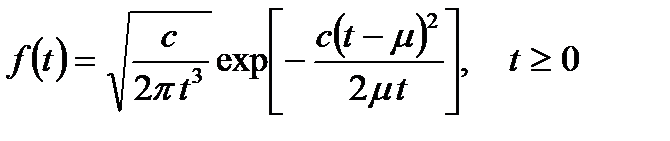                                  ,                                     (6.24)

где 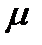– параметр положения;

 – параметр формы.

Обратное гауссовское распределение с параметром положения 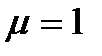 называется распределением Вальда.

На рис 6.11 показан график плотности распределения.

Числовые характеристики:

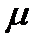 – математическое ожидание;

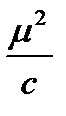 – дисперсия;

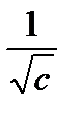 – коэффициент вариации.

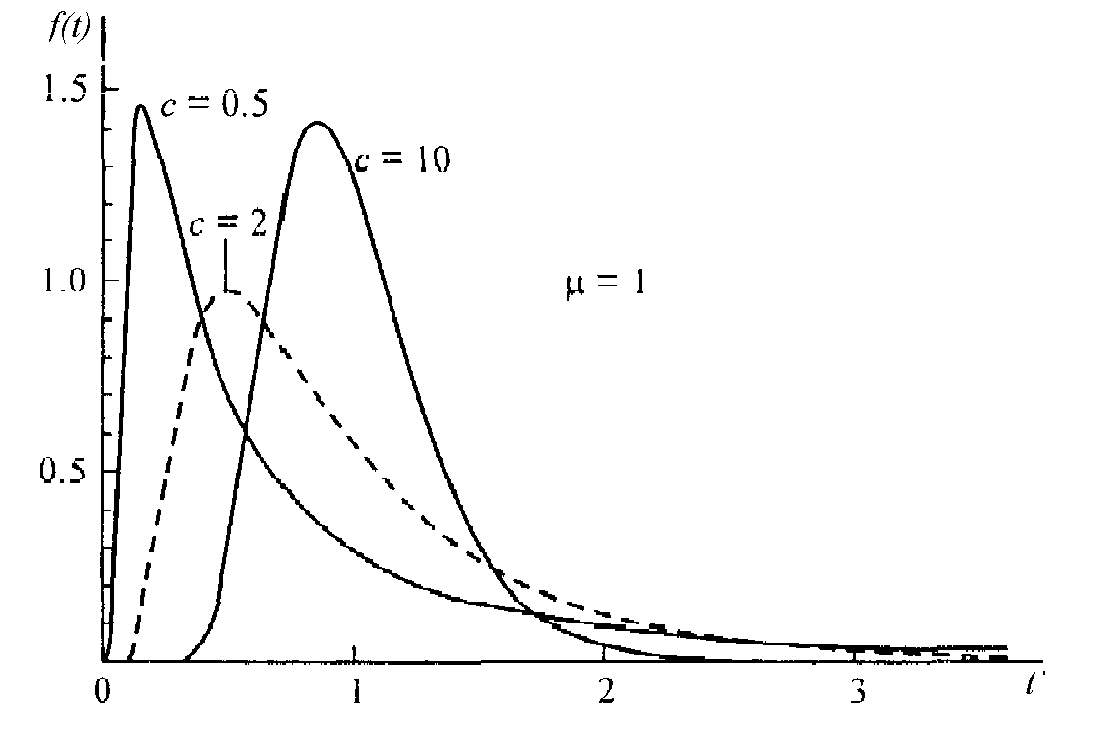
Рис. 6.11. График плотности обратного гауссовского распределения

На рис 6.12 показан график интенсивности отказов

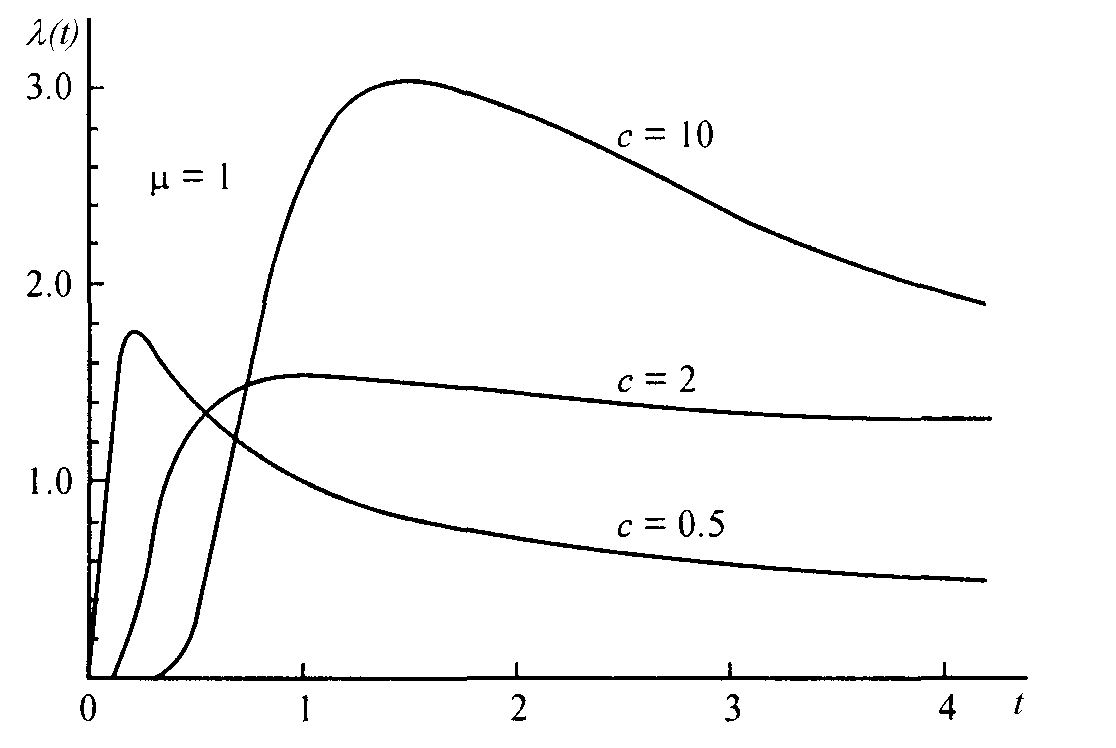
Рис. 6.12 График интенсивности отказов обратного гауссовского распределения

Обратное гауссовское распределение находит применение в задачах анализа надёжности, долговечности и выживания. При определённых сочетаниях параметров функция обратного гауссовского распределения оказываются достаточно близкой к функции логарифмически нормального распределения. В тоже время плотности распределения имеют заметное отличие, а соответствующие функции интенсивности отказов в обоих случаях являются колоколообразными и отличаются очень сильно. Следует отметить, что с этими двумя моделями может конкурировать трехпараметрическая модель обобщенного распределения Вейбулла, функция интенсивности которого может принимать все известные виды и, в частности, колоколообразной формы. 

Лекция №7. Элементы теории надежности в технической диагностике. Часть четвертая

Равномерное распределение

Плотность равномерного распределения будет равна:

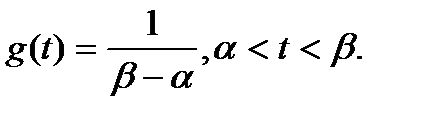                                                                                                       (7.1)

Числовые характеристики:

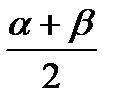 – математическое ожидание;

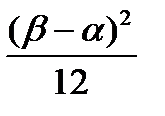 – дисперсия;

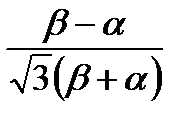– коэффициент вариации;

На рис 7.1 показан график плотности распределения.

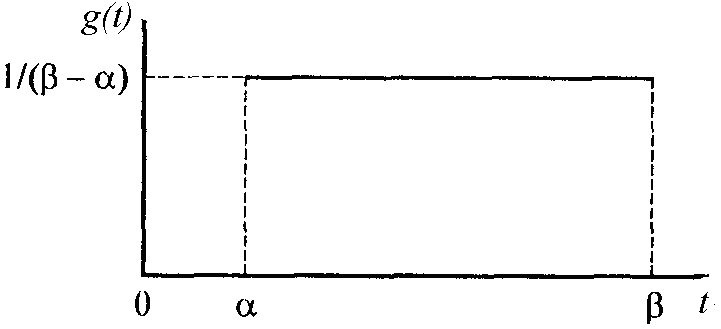
Рис. 7.1. График плотности равномерного распределения

На рис 7.2 показан график интенсивности отказов

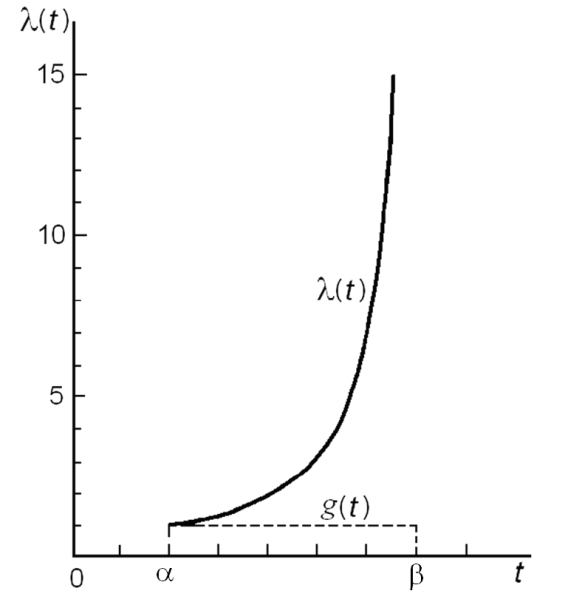
Рис. 7.2. График интенсивности отказов равномерного распределения

Распределение Вейбулла

Плотность распределения Вейбулла равна:

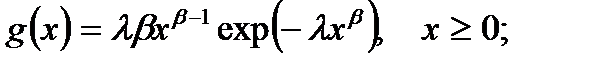                                                                                   (7.2)

Функция распределения:

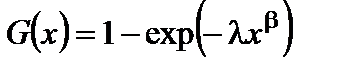                                        .                                                             (7.3)

Начальные моменты 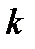 – го порядка определятся соотношениями

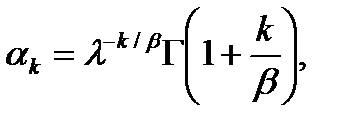                                                                                                         (7.4)

Параметры:

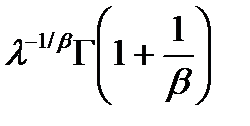 – математическое ожидание;

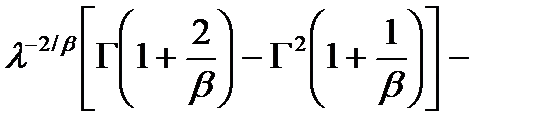дисперсия;

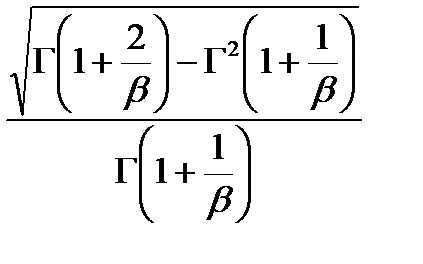 – коэффициент вариации;

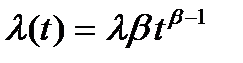 – интенсивность отказов;

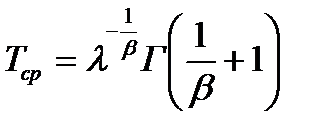 – среднее время безотказной работы.

Здесь 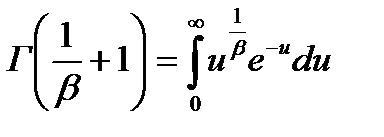 – гамма функция.

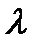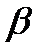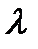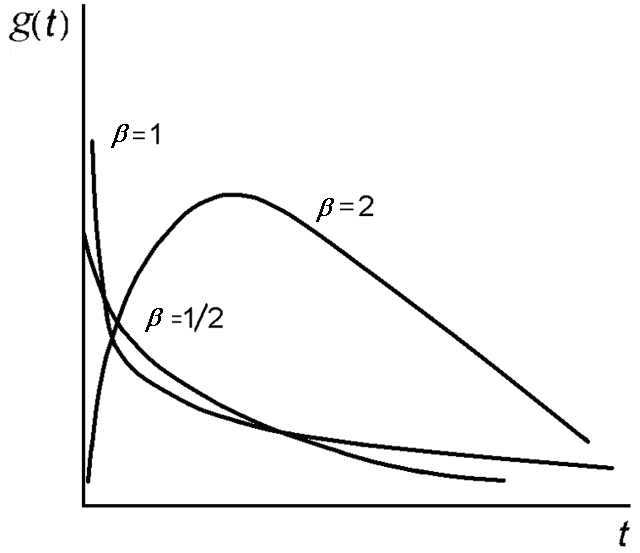
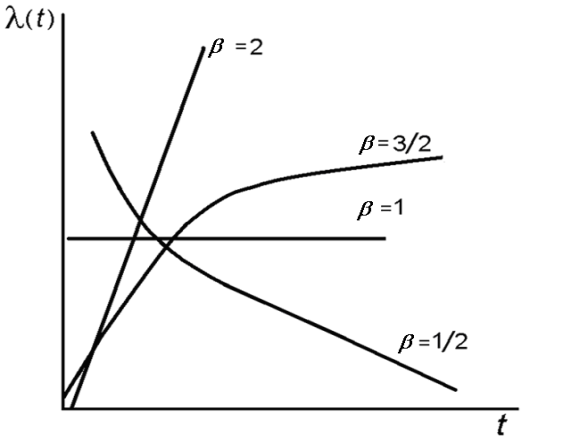
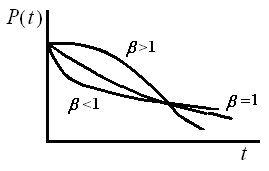
Распределение Вейбулла имеет два параметра:  и . Параметр  определяет масштаб, при его изменении кривая распределения «сжимается» или «растягивается». Обычно значения 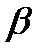 выбирают от 1до 2. На рис 7.3 представлены графики плотности распределений времени безотказной работы, интенсивности отказов и функции надежности.

При определенном подборе параметра формы 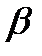 из этого распределения можно получить все три участка -образной кривой интенсивности отказов: при 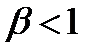 имеем приработочный участок (интенсивность отказов убывает), при  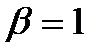– участок с постоянной интенсивностью; при  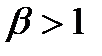– износовый участок (интенсивность отказов возрастает). Поэтому, применяя сплайны распределения Вейбулла с различными 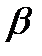, можно описать 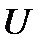-образный вид интенсивности отказов. Большинство экспериментальных данных по долговечности хорошо описываются этим распределением. Как известно, Вейбулл независимо от асимптотической теории, применил это распределение для анализа усталостных испытаний. Из этого распределения, как частные случаи,

                                                                    а

                                                                    б

                                                                   в

Рис. 7.3.Графики распределения Вейбулла при .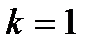

 а – кривые плотности распределения времени безотказной работы;

б – интенсивности отказов;

в – функции надежности.

Далее следуют распределения Рэлея ( 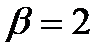) и экспоненциальное распределение ( 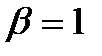). При определенных значениях параметров им могут быть приближенно описаны нормальное и логарифмически нормальное распределения. Распределение Вейбулла использовалось в задачах моделирования таких характеристик, как то: предел текучести босфорской стали, прочность волокон индийского хлопка, усталостная долговечность стали, рост взрослых уроженцев Британских островов мужского пола, размер бобов. Оно известно как распределение Вейбулла –Гнеденко, а также как распределение Фреше. Это распределение применяется для описания надежности шариковых подшипников, описания модели слабейшего звена в группе последовательно соединенных элементов, усталостных явлений (долговечности) механических конструкций, деформирования и разрушения материалов со случайной микроструктурой, а также при обработке результатов механических испытаний для описания функции распределения параметра прочности: сопротивления усталости, ползучести, изнашивания, коррозии и т.п.