Важнейший вопрос в теории надежности – выбор распределения времени безотказной работы исследован в настоящее время недостаточно. Вместе с тем во многих случаях за время эксплуатации или испытаний на надежность успевают отказать лишь незначительная часть первоначально установленных элементов. Полученным статистическим данным соответствует «левая ветвь» экспериментального распределения. Поэтому значения числовых характеристик, найденные в результате обработки опытных данных, сильно зависят от предполагаемого распределения времени безотказной работы. Например, при различных предположениях о виде распределения времени безотказной работы, значения среднего времени безотказной работы элементов, вычисленные по одним и тем же опытным данным, могут отличаться в сотни раз. Для выбора распределения времени безотказной работы целесообразно использовать информацию об изменениях в элементах перед возникновением отказов. Для этого необходимо знать, в результате каких физических процессов появляется соответствующее распределение. Иначе говоря, выбранному распределению времени безотказной работы должна соответствовать определенная модель приближения элемента к отказу. Желательно, чтобы эти модели были физическими, т.е. обобщали основные особенности физических процессов приближения к отказам (а также допускали возможность воспроизведения этих процессов в лаборатории). При рассмотрении математических вопросов надежности используют модели, которые условно можно назвать «вероятностными». Обычно вероятностные модели создаются для «обоснования» готовых, существовавших ранее, математических моделей. Примером такой модели может служить «гипотеза чистого разрушения» Г. Вейса, согласно которой отказ элемента наступает после повреждения определенного числа 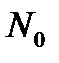 нитей, участков и т.п., причем каждая нить, участок и т.п. выходит из строя независимо от других нитей и т.п. Если вероятность выхода из строя одной нити в интервале времени 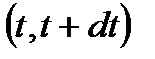, когда остается  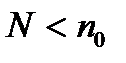нитей, равна 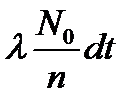, то имеет место гамма-распределение времени безотказной работы элементов

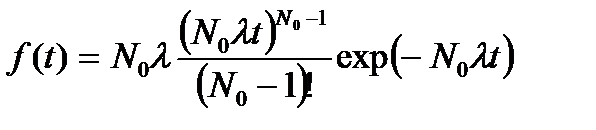                                .                                              (7.25)

В «гипотезе чистого разрушения» вводится предположение о вероятности отказа отдельных частей элементов, а не об изменении физических параметров. Существуют и другие вероятностные модели развития отказов. Эти модели нисколько не облегчают выбор типа теоретического распределения времени безотказной работы. Для осуществления такого выбора необходимы сведения о физических процессах приближения к отказам. Знание функции распределения и определяющих параметров необходимо при выполнении многих вероятностно-статических расчетов. Особенно большое значение имеет обоснование вида функции распределения на этапе проектирования технических устройств, когда разработчик располагает ограниченными статистическими данными. При известном виде распределения достаточно определить его характеристики. Для решения последней задачи требуется значительно меньше экспериментальных данных, чем для установления вида функции распределения. Вот почему большое значение приобретает анализ путей обоснования распределений. При этом важное значение имеет обоснование распределений исходя из сущности исследуемых явлений и процессов. Под теоретическим распределением понимается распределение случайной величины, которое получено в виде аналитического выражения для вполне определенной конкретной схемы, отображающей реальную сущность исследуемого процесса или явления. Большое внимание уделяется теоретическому обоснованию видов распределения для следующих схем условий возникновения случайных величин:

– случайная величина является суммой большого числа случайных слагаемых;

– случайная величина является функцией одной или нескольких случайных величин;

– случайная величина образуется в результате преобразований одной или нескольких случайных величин (например, путем отбора больших или меньших отклонений или нескольких исходных).

Среди разновидностей суммы случайных величин простейшей является следующая. В состав суммы входят одна группа слагаемых, структура суммы не изменяется ни от времени, ни от других аргументов, число слагаемых при теоретическом рассмотрении может быть устремлено к бесконечности, слагаемые взаимно независимые или слабо зависимые и равномерно пренебрегаемые в пределе. Количественным выражением условия равномерной пренебрегаемости слагаемых в пределе служат различно формулируемые условия, сущность которых сводится к ограниченной роли отдельных слагаемых. При соблюдении этих условий и устремлении числа слагаемых к бесконечности распределение суммы случайных величин в соответствии с центральной предельной теоремой описывается нормальным распределением (распределением Гаусса).

Если схема образования случайной величины сводится к произведению большого числа примерно одинаковых по своему влиянию положительно распределенных величин, то предельным законом такой случайной величины является логарифмически нормальный закон.

В соответствии с другим подходом – моделью слабейшего звена каждый элемент считается составленным из звеньев. Элемент отказывает, если выходит из строя хотя бы одно звено. В предположении, что долговечности всех 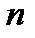 звеньев – независимые случайные величины, имеющие одно и то же распределение 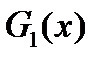, соответствующая функция распределения элемента определяется как

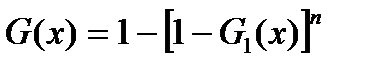                                                .                                                   (7.26)

При большом 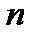 для обоснования вида распределения можно использовать асимптотические распределения теории экстремальных значений, в соответствии с которой существует три типа предельных распределений для наименьших (наибольших) значений.

Асимптотические распределения строго обоснованы для независимых случайных величин. В действительности же времена отказов, на которые условно разбивается элемент, будут зависимыми. В этом случае необходимо находить функции распределения соответственно наибольшего и наименьшего значений совокупности зависимых случайных величин.

Рассмотрим выбор распределения по эмпирическим данным. Наиболее простым, но весьма приближенным методом оценки согласования с выбранным распределением является графический способ, однако он является субъективным и используется лишь в качестве первого приближения. Использование более строгих аналитических критериев согласия, зачастую теряет свою значимость ввиду того, что параметры предполагаемого распределения заранее не известны, а оцениваются по эмпирическим данным и поэтому целесообразно использовать еще другой критерий. В основе критериев лежат статистические гипотезы: параметрические (предположения относительно параметров распределения) и непараметрические (относительно вида распределения). При этом рассматривается нулевая гипотеза (отсутствие различия) и альтернативная (есть различия), которая принимается после того, как отвергается основная. Реализация этих гипотез осуществляется сравнением значений критериев, установленных теоретическим путем с их значениями, вычисленными по экспериментальным данным. Если последние не превышает критического значения, то отсутствуют обоснования, чтобы отвергнуть нулевую гипотезу.

При большом числе наблюдений статистический материал подвергается обработке – строится статистический ряд. Для этого весь диапазон значений случайной величины делится на интервалы или разряды (обычно для получения разрядов промежуток 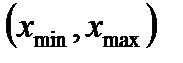 между крайними элементами выборки разбивается на  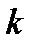частичных промежутков-разрядов равной длины 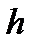) и определяется число  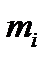элементов выборки , попавших в данный  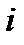– й разряд. Это число (частота попадания) делится на общее число наблюдений  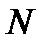и находится относительная частота попадания элементов в разряды:

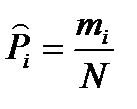                                                   .                                                                       (7.27)

Сумма этих частот равна единице.

Статистический ряд часто оформляется в виде так называемой гистограммы иначе диаграммы распределения частот попадания выборочных данных в заранее выбранные промежутки (разряды). Сопоставляя гистограмму с графиками теоретических плотностей распределения можно выдвинуть предварительное суждение о распределении изучаемой случайной величины и осуществить проверку гипотезы. Гистограммы служат удобным средством обобщения статистических данных, число элементов которых может достигать многих тысяч. Для построения гистограммы по оси абцисс откладываются разряды, и на каждом из разрядов как их основании строится прямоугольник, площадь которого равна относительной частоте данного разряда. Для построения гистограммы нужно относительную частоту каждого разряда разделить на его длину и полученное число взять в качестве высоты прямоугольника. В случае равных по длине разрядов высоты прямоугольников пропорциональны соответствующим частотам. Полная площадь гистограммы равна единице. Существует ряд рекомендаций по выбору значений 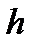 или числа разрядов 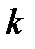. Ширину разряда рекомендуется выбирать в зависимости от величины выборочного среднего квадратического отклонения  данных по формуле

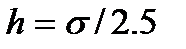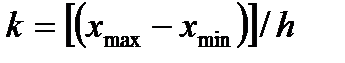                                  , .                                                (7.28)

Другие рекомендации связаны с выбором числа разрядов по формулам

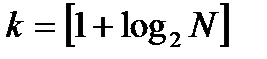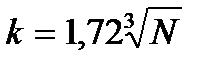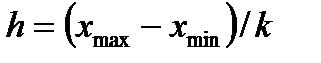                   , , .                                    (7.29)

Рассмотрим обоснование вида распределения ресурса на основе непараметрических гипотез (критерий ).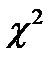

При использовании критерий 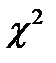 имеющаяся выборка с числом наблюдений  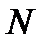подразделяется на  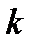разрядов (интервалов). Подсчитывается число наблюдений , попавшее в 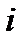 – ый интервал. При этом выполняется соотношение 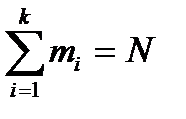. Эмпирические вероятности попадания случайной величины  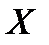в 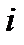 – ый интервал находится по формуле

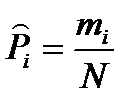                                                            .                                                              (7.30)

При небольшом 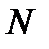 рекомендуется следующая формула

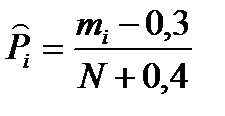                                                    .                                                         (7.31)

Предположим, что выдвигается гипотеза о том, что непрерывная случайная величина  имеет распределение 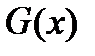. Теоретическая вероятность попадания случайной величины  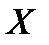в i-й интервал вычисляется по формуле

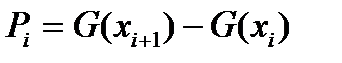                                                    .                                                  (7.32)

Определяются значения теоретических частот 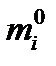 путём умножения теоретических вероятностей на объем выборки

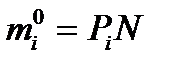                                                            .                                                          (7.33)

Если имеющиеся эмпирические данные подтверждают гипотезу о справедливости принятого теоретического распределения, то согласно 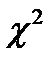-критерию должно выполняться неравенство

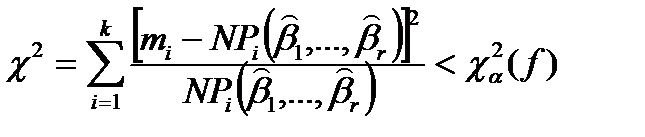                                         ,                                     (7.34)

где 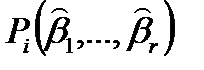 – вероятность попадания случайной величины в  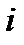– ый интервал, найденные по оценкам параметров при выбранном распределении;

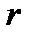 – число неопределенных параметров, оцениваемых по выборочным данных .

Значения 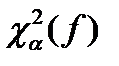 приводятся в таблицах для различного числа степеней свободы  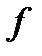(оно равно числу разрядов 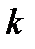, уменьшенному на число  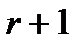при различных уровнях значимости 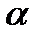). Значения  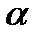в каждом конкретном случае устанавливаются отдельно. Наиболее часто используются значения .

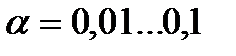При нормальном распределении

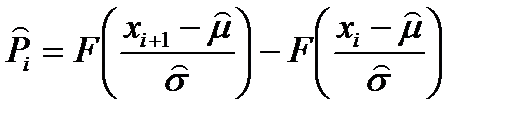                                  ,                                                    (7.35)

а число степеней свободы .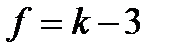

Если параметры теоретического распределения известны заранее, то используется критерий согласия Колмогорова. При неизвестных параметрах он может быть использован только для некоторых функций распределения. При использовании этого критерия в качестве меры расхождения используется модуль максимальной разности между эмпирическим 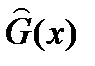 и теоретическим распределением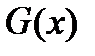

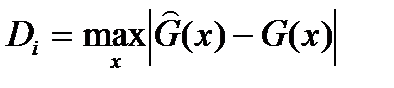                                          ,                                                       (7.36)

являющейся статистикой Колмогорова.

По выборочным данным (вариационному ряду 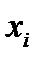) вычисляется эмпирическая функцию распределения

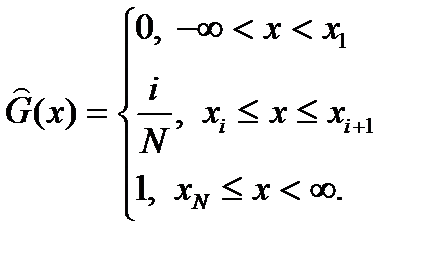                                      .                                                       (7.37)

При 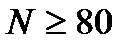 случайная величина  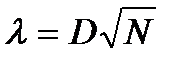описывается распределением 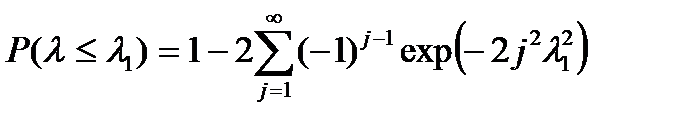. Если оказывается, что 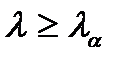, то уровнем значимости  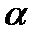критерий отбрасывает в нулевую гипотезу. В противном случае ( 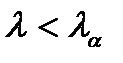) – гипотеза принимается.

Для приближенной проверки гипотезы о нормальности распределения вычисляют выборочные показатели ассиметрии 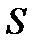 и эксцесса 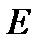, а также их средние квадратические отклонения. Последнее вычисляются по формулам :

                                   ,

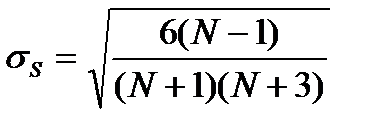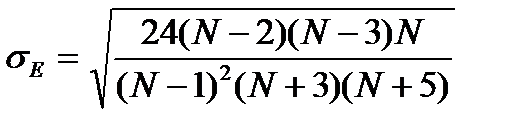                                         .                                            (7.38)

Если абсолютные величины статистик 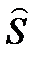 и 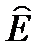 равны или меньше своих средних квадратических отклонени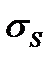й  и 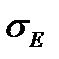, то гипотезу нормальности отвергают.

При этом можно использовать критерий 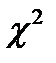, вычисляемый по формуле:

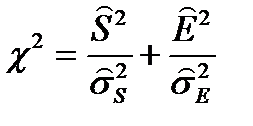                                                        ,                                                       (7.39)

который сопоставляют с табличным значением .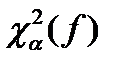

Можно использовать более точные формулы:

                                       ,

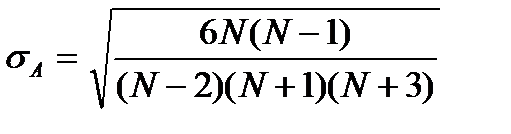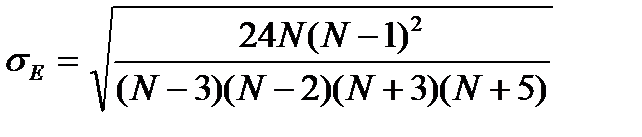                                ,                                          (7.40)

где 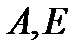 - несмещенные оценки для показателей ассиметрии и эксцесса.

Нулевая гипотеза принимается, есл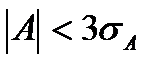и

                                                        и 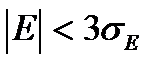.                                            (7.41)

Специально для двухпараметрического распределения Вейбулла критерий согласия разработали Манн и др. В этом случае нулевая гипотеза состоит в том, что эмпирическое распределение описывается распределением Вейбулла.

Пусть 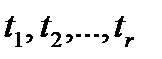 наработки до отказа, полученные при прекращении испытаний в момент появления  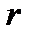– го отказа. Обозначим 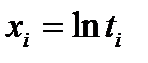. Тогда статистика, лежащая в основе этого критерия, имеет вид:

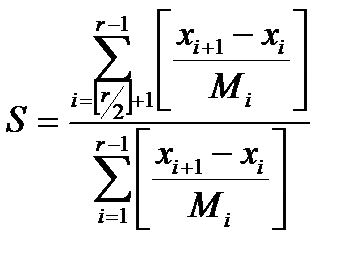                                                  ,                                                  (7.42)

где 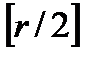обозначает наибольшее целое число .

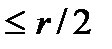Значения 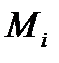, а также критические значения  приводятся в справочной литературе.

Лекция №8. Элементы теории надежности в технической диагностике. Часть пятая

Расчет надежности систем

Рассмотрим невосстанавливаемую систему, в которой при выходе из строя одного элемента нарушается работа всей системы. Первичный отказ одного элемента может, вообще говоря, привести к повреждению других элементов. Однако эти вторичные отказы не учитываются, так как они возникают в системе, которая уже вышла из строя из-за первичного отказа. Обычно предполагается, что отказы элементов являются событиями независимыми. При этом довольно грубом допущении имеем согласно правилу умножения вероятностей:

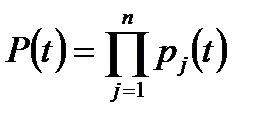                                                ,                                                                (8.1)

где: 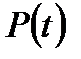 – функция надежности системы;  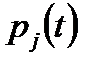– функция надежности 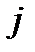– го элемента;  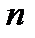– число элементов.

Элементы, отказ которых не ведет к отказу системы, не учитываются, т.е. не входят в число .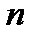

Получать функцию надежности системы 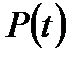 непосредственным вычислением по формуле (8.1) практически очень трудно, особенно при большом числе элементов в системе. Поэтому возникает вопрос о практическом методе расчета надежности систем.

Рассмотрим систему, состоящую из 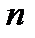 разнородных элементов. Функция надежности системы будет определяться выражением:

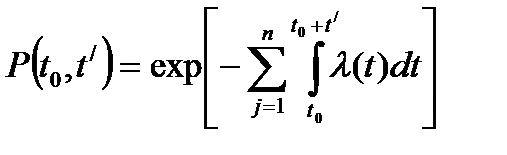                                                                                               (8.2)

или

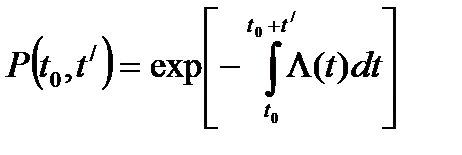                                                                                                   (8.3)

где 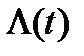 – интенсивность отказов системы равна сумме интенсивностей отказов элементов

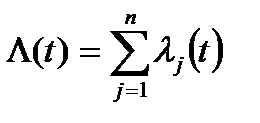                                              .                                                 (8.4)

Для системы из одинаковых элементов

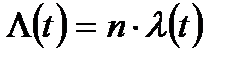                                                                                                            (8.5)

и соответственно:

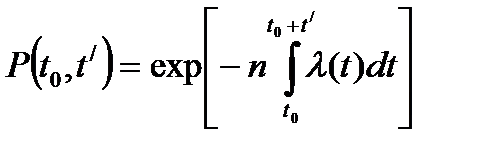                                                                                      (8.6)

Вычисление функции надежности системы сводится к суммированию площадей 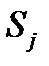 под графиками интенсивности отказов элементов и нахождению по формуле  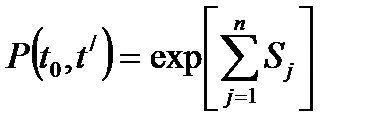значения вероятности безотказной работы. Процесс вычисления функции надежности системы значительно усложнится, если использовать плотности распределения времени безотказной работы элементов 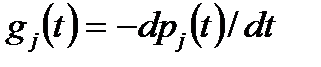. Функция надежности системы  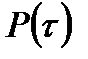в этом случае в соответствии с формулой (6.17) будет определяться выражением

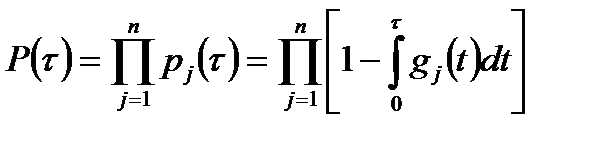                                          .                                     (8.7)

Уже по виду формулы (7.206) можно заключить, что вычисление функции надежности системы по плотностям распределения времени безотказной работы элементов в общем случае приводит к очень громоздким вычислениям. При малых значения 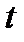 можно не делать различия между  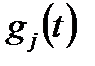и 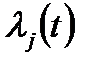, так как в этом случае из выражения

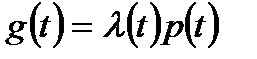                                                      .                                                      (8.8)

Следует, что 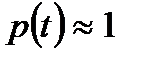 и 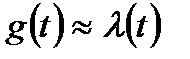, а для  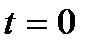значения  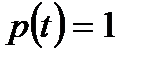и .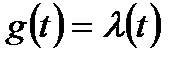

Согласно (8.8) всегда справедливо неравенство 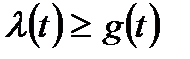. Если 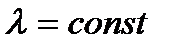, то функция  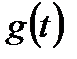убывает с течением времени работы по экспоненте.

Таким образом, надежность элемента или системы определена, если известна одна из трех характеристик времени безотказной работы (времени работы до первого отказа):

– функция надежности ;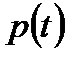

– плотность вероятности времени безотказной работы ;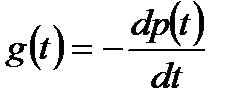

– интенсивность выхода из строя .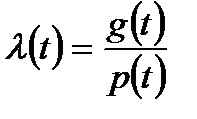

Предсказание надежности состоит в вычислении одной из этих характеристик. Используется та из них, которую более удобно применять в конкретной задаче.

Кроме перечисленных выше трех характеристик времени безотказной работы для измерения надежности восстанавливаемых систем (систем многократного действия), которые после появления отказа восстанавливаются и затем вновь продолжают эксплуатироваться, используется интенсивность потока отказов (интенсивность возобновления работы систем). Автоматизированные системы контроля насчитывают в своем составе порядка 50000 мелких элементов. Изменение характеристик безотказности таких устройств очень хорошо описывается экспоненциальным законом. При этом определенные элементы могут и не проявлять признаков экспоненциального закона. Но если отказавшие элементы заменяются новыми, то вследствие эффекта перемешивания возрастов отказы устройства в целом будут подчиняться экспоненциальному распределению.