В логических схемах для расчета надежности систем встречаются связи между элементами, которые не удается свести только к последовательным или параллельным соединениям. Например, пусть имеется система, безотказная работа которой обеспечивается следующей комбинацией элементов (табл. 2).

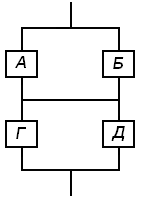
Этой словесной формуле соответствует логическая схема рис. 9.1, соединения которой не удается свести только к последовательным или параллельным.

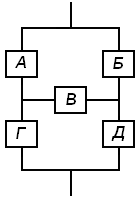
Рис. 9.1. Пример логической схемы для расчета надежности системы

Для вычисления надежности систем, имеющих логические схемы надежности, аналогичные схеме рис. 9.1, целесообразно применять формулу полной вероятности. При использовании этой формулы учитываются гипотезы: 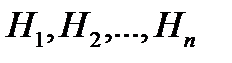 – несовместные события, образующие полную группу. Вместе с одним из этих событий может произойти рассматриваемое событие  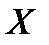– безотказная работа системы в течение заданной наработки 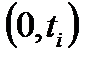. Вероятность появления события  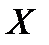равна сумме произведений вероятности каждой гипотезы  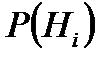на условную вероятность  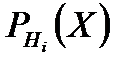события при этой гипотезе:

.

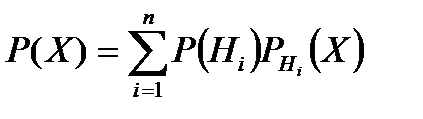(9.1)

Для использования формулы полной вероятности при расчете надежности выберем определенный 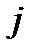 – ый элемент логической схемы системы и рассмотрим две гипотезы:

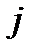 –  – ый элемент безотказно работает в течение заданного времени;

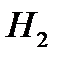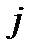 –  – ый элемент отказал в течение заданного времени.

В рассматриваемом случае событие 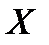 – безотказная работа системы. Вероятности гипотез:

; ,

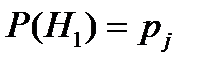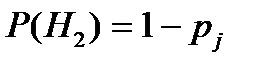(9.2)

где 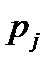 – вероятность безотказной работы  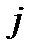– го элемента в течение заданного времени.

Вероятность безотказной работы системы:

,

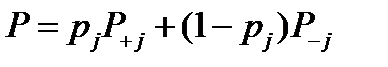(9.3)

где 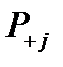,  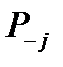– условные вероятности безотказной работы системы при безотказной работе  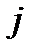– го элемента и при отказе этого элемента соответственно.

Зависимость (9.3) можно сформулировать в виде следующего правила: вероятность безотказной работы системы равна произведению вероятности безотказной работы элемента на условную вероятность безотказной работы системы при безотказной работе данного элемента плюс произведение вероятности отказа элемента на условную вероятность безотказной работы системы при отказе данного элемента.

Применим формулу (9.3) к системе, логическая схема которой представлена на рис. 9.1. В качестве гипотез возьмем безотказную работу и отказ элемента В. Для вычисления вероятносте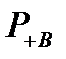й  и 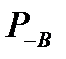 составим условные логические схемы, изображенные на рис. 9.2.

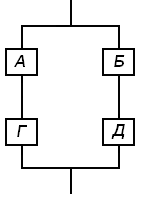
                                       a                                               б

Рис. 9.2. Условные логические схемы для расчета надежности системы, имеющей изображенную на рис. 9.1 схему

а – при безотказной работе элемента В; б – при отказе элемента В

Эти схемы получены из схемы рис. 9.1 при предположениях о безотказной работе элемента В и об отказе элемента В. В соответствии со схемами рис. 9.2 имеем:

,                                    .

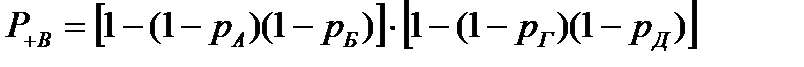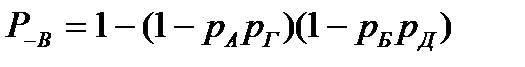(9.4)

Подставив в формулу (9.3) значения 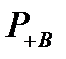 и 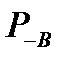, получим функцию надежности системы:

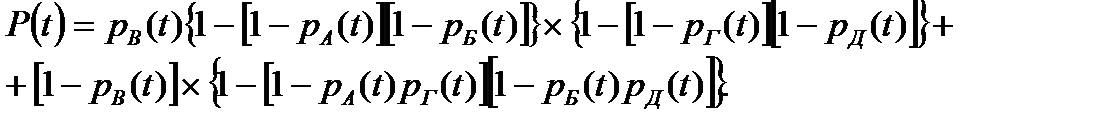
(9.5)

При 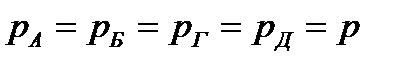 имеем после преобразований:

.

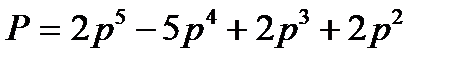(9.6)

В ряде случаев целесообразно применять формулу (9.3) последовательно, шаг за шагом. Для этого при вычислении условных вероятносте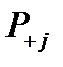й  и 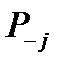 вновь выбирают определенный элемент  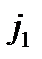и производят вычисление 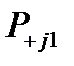,  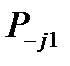по формуле, аналогичной (9.3), и т.д.