| Юноши (n1=7)
| Ранг
| Девушки (n1= 7)
| Ранг
| ||
| № | Оценка по психометрии | № | Оценка по психометрии | ||
| 1 | 710 | 5,5 | 1 | 715 | 7 |
| 2 | 720 | 10 | 2 | 730 | 13 |
| 3 | 716 | 8 | 3 | 730 | 13 |
| 4 | 700 | 1 | 4 | 718 | 9 |
| 5 | 708 | 3,5 | 5 | 710 | 5,5 |
| 6 | 703 | 2 | 6 | 708 | 3,5 |
| 7 | 730 | 13 | 7 | 724 | 11 |
|
| R1=43 |
| R2=62 | ||
Выбираем уровень значимости α =0,05 и формулируем нулевую и альтернативную гипотезы.
Н0: Результаты психометрии у мужчин не отличаются от результатов психометрии у женщин.
Н1: Результаты психометрии у мужчин отличаются от результатов психометрии у женщин (двусторонняя критическая область12).
12 В рамках решаемой задачи не выдвигается гипотеза о том, что у одних результаты психометрии лучше, а у других хуже. Для Даниила и Юлии важно проверить сам факт наличия различий в зависимости от пола. Поэтому используется двусторонняя критическая область.
Для проверки нулевой гипотезы вычислим два значения:
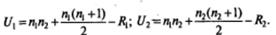
Из таблицы находим n1= n2=7; R 1= 43; R 2 = 62. Подставляем эти значения в формулы и находим:
. 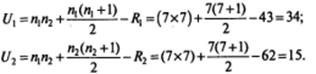
Из двух значений U1 и U2 выбираем меньшее (U = 15) и используем его в дальнейших расчетах13.
13 Здесь также можно использовать описанный выше подход, основанный на прямом сравнении значений в обеих выборках. В случае совпадения сравниваемых значений результат сравнения принимается равным 0,5.
При наличии в результатах k групп связанных рангов значение z вычисляется по скорректированной формуле:
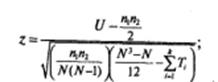
где N= n1= n2; Ti = ( ti 3 - ti) /12, ti — число связанных рангов в каждой из k групп.
Как отмечалось, мы имеем три группы связанных рангов. В первой группе!; два связанных ранга, во второй группе также два связанных ранга и в третьей группе три связанных ранга. Тогда t 1 = 2; t2 = 2; t3 = 3.
Определим значение 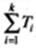 :
:
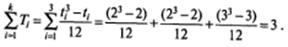
Подставим в формулу для z все необходимые значения:
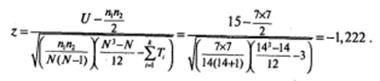
По таблице 1 (Приложение 2) для z -распределения находим, что левее значения z.= − 1,222 лежит вероятность р =0,111 (левосторонняя критическая область). Поскольку альтернативная гипотеза сформулирована для двусторонней критической области, удваиваем полученное значение: р =0,222. Данное значение больше выбранного уровня значимости α =0,05, поэтому у нас нет оснований отклонить нулевую гипотезу. Результаты психометрии у мужчин не отличаются от результатов психометрии у женщин.
ВКЛЮЧАЕМ КОМПЬЮТЕР...
В программе SPSS производится вычисление значения z по одной из двух приведенных выше формул, в зависимости от того, имеются ли в результатах связанные ранги или нет.
Перейдем к программе SPSS и рассмотрим первый пример. В переменной «Выборка» (sample) укажем принадлежность к первой (1) или второй (2) выборке. В переменной «Тревожность» (anxiety) укажем значения предродовой тревожности для участников обеих выборок. Дальнейшая последовательность действий и результат показаны на рис. 6.9-6.11.

Рис. 6.9. Выбор требуемой статистической процедуры




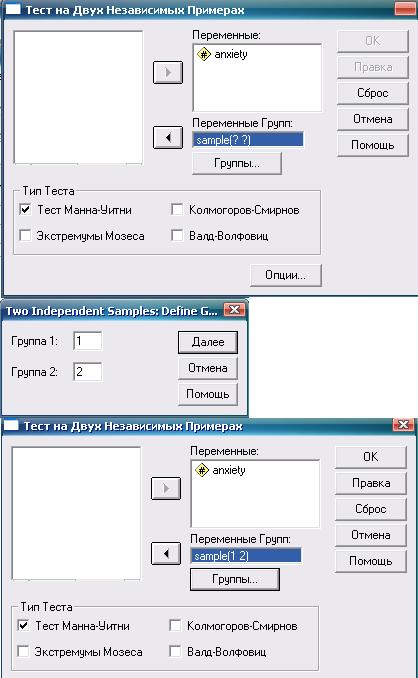
Рис. 6.10. Тест Манна—Уитни: требуемые действия и настройки
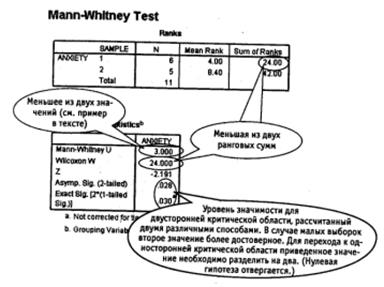
Рис. 6.11. Тест Манна — Уитни: результат
Для второго примера (случай связанных рангов) введем переменную «Пол» (gender), в которой 1 соответствует мужчинам, 0 — женщинам. Результаты психометрического экзамена поместим в переменную «Тест» (test). Проделаем те же действия, что в предыдущем примере (на этапе кодировки групп вместо обозначений 1 и 2 используем кодировку 0 и 1 и получим следующий результат (рис. 6.12).
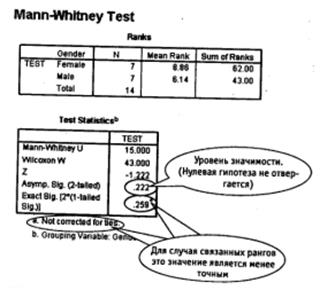
Рис. 6.12. Тест Манна — Уитни: результат (случай связанных рангов)
Дата: 2018-12-21, просмотров: 734.