| 14 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 23 | 23 | 25 | 26 | 27 | 30 | 31 | 32 | 35 | 37 | 38 |
| А | А | В | В | В | А | А | А | А | В | В | В | В | В | В | В | А | А | А | А |
В упорядоченной последовательности результатов двух выборок можно выделить 5 серий, говорящих о том, насколько обе выборки «перемешаны»:
АА, ВВВ, АААА, ВВВВВВВ, АААА.
Поскольку в данном тесте мы имеем дело с сериями из нескольких одинаковых значений, то вновь используем таблицу 6 (Приложение 2) для теста последовательностей. Сравниваем полученное число серий (R=5) с приведенным в первой строчке значением для случая n1= n2= 10: Rкритнч = 6 (в таблице приведены критические значения, соответствующие уровню значимости α =0.05).
Если эмпирическое значение R больше критического, нет оснований отвергнуть нулевую гипотезу. Если эмпирическое значение R меньше критического или равно ему, нулевая гипотеза отвергается и принимается альтернативная18.
18 В данном случае мы вновь встречаемся с ситуацией, когда правило принятия решения после сравнения Кэмпир и Ккритич носит «обратный» характер: нулевая гипотеза отвергается, когда Кэмпир меньше Ккритич.
В нашем случае Rэмпир=5, Rкритич =6. Поскольку Rэмпир < Rкритич, нулевая гипотеза отвергается. Диеты отличаются друг от друга по своей эффективности.
Как видно из табл. 6, она предназначена для выборок, содержащих не более 20 значений каждая. В случае выхода размеров выборок за эти пределы, необходимо использовать общую расчетную формулу для теста Вальда—Волфовица. Если каждая выборка содержит более 30 значений, то вычисляется значение г и используется статистическая таблица для z -распределения (табл. 1, Приложение 2). Необходимые расчетные формулы приведены ниже.
При использовании теста Вальда—Волфовица зачастую возникает дополнительная проблема, затрудняющая его применение.
Рассмотрим пример.
Группе детей (5 мальчиков и 5 девочек) был предложен набор из 10 головоломок (популярные задачи на перекладывание спичек). За отведенное время группа справилась с заданием следующим образом (приведено число решенных головоломок; табл. 6.21).
Таблица 6.21
Число решенных головоломок
| Мальчики | Девочки |
| 7 | 6 |
| 5 | 7 |
| 5 | 5 |
| 4 | 6 |
| 8 | 3 |
Если сравнить обе группы, то в них можно увидеть одинаковые (связанные) результаты. При объединении обеих групп и упорядочивании результатов ясно, в какой последовательности записывать повторяющиеся результат относящиеся к разным группам.
Здесь возможны несколько вариантов:
| 3 | 4 | 5 | 5 | 5 | 6 | 6 | 7 | 7 | 8 |
| Д | М | М | М | Д | Д | Д | Д | М | М |
| 3 | 4 | 5 | 5 | 5 | 6 | 6 | 7 | 7 | 8 |
| Д | М | М | Д | М | Д | Д | Д | М | М |
| 3 | 4 | 5 | 5 | 5 | 6 | 6 | 7 | 7 | 8 |
| Д | М | Д | М | М | Д | Д | Д | М | М |
| 3 | 4 | 5 | 5 | 5 | 6 | 6 | 7 | 7 | 8 |
| Д | М | Д | М | М | Д | Д | М | Д | М |
| 3 | 4 | 5 | 5 | 5 | 6 | 6 | 7 | 7 | 8 |
| Д | М | Д | М | М | Д | Д | М | Д | М |
Все варианты являются равноправными, но в первом из них 4 серии, следующих 6 серий и в двух последних 8 серий. Как известно, чем больше серий, тем сильнее «перемешаны» результаты, тем меньше шансов выявить различия между выборками.
К сожалению, однозначного решения проблемы совпадающих результат не существует [Siegel, 1956]. В ряде случаев рекомендуется записать все возможные варианты упорядочивания с учетом совпадающих результатов, затем произвести статистическую проверку для каждого из них и вынести окончательное решение о судьбе нулевой гипотезы по результатам проверки [Runyon, 1977]. При этом различных вариантов записи упорядоченных результатов может быть до нескольких десятков (в нашем простом примере их уже 5)19.
19 Использование программы SPSS избавляет от этих трудностей.
ВКЛЮЧАЕМ КОМПЬЮТЕР...
В программе SPSS на основе сведений о размере выборок n1и n2 и числе серий R рассчитывается вероятность получения такого результата. Для этого использует следующая формула, меняющаяся в зависимости от того, имеем ли мы дело с четными или нечетными значениями:
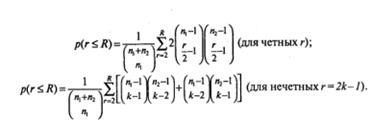
Итоговая вероятность равна сумме «четных» и «нечетных» частей этой формулы. В нашем примере n1= n2= 10; R =5. Значение r меняется от 2 до 5. Если r =3, это означает r =(2х2) -1, то есть k:=2. Если r =5, это означает r =(2х3) -1, то есть k =3.
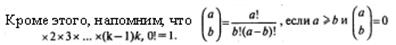
Подставим в формулу все необходимые данные.
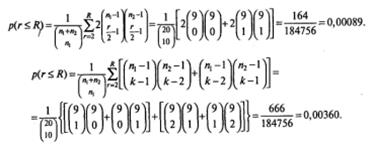
Объединяем «четный» и «нечетный» результаты:
р(r≤R) = 0,00089 + 0,00360 = 0,00449 = 0,004.
Кроме вычисленного значения вероятности (соответствующего односторонней критической области), которое сравнивается с выбранным уровнем значимости α, вычисляется значение z с учетом тех поправок, которые были рассмотрены в параграфе 3.4:
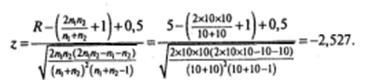
Если каждая выборка содержит более 30 значений, то различия между вычисленным значением вероятности и значением вероятности, полученным на основе z-распределения (табл. 1, Приложение 2), становится несущественным. Перейдем к программе SPSS. В переменной «Группы» (groups) принадлежность участников эксперимента к первой или второй группе обозначена как 1 или 2. В переменной «Время» (time) указано время (в неделях), в течение которого вес был снижен на 20 кг. Дальнейшая последовательность действий и конечный результат показаны на рис. 6.17—6.19.

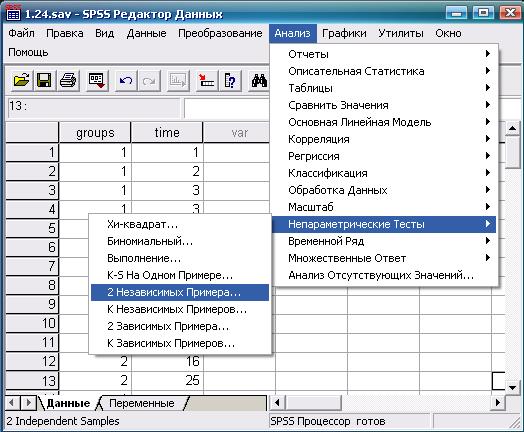
Рис. 6.17. Выбор необходимой статистической процедуры


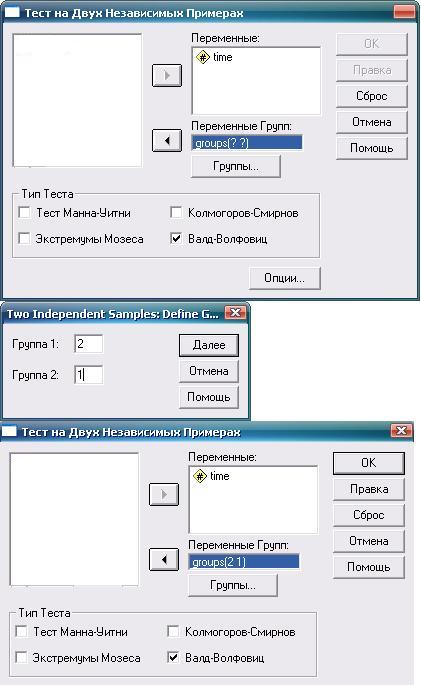
Рис. 6.18. Тест Вальда—Волфовица: необходимые действия и настройки.

Рис. 6.19. Тест Вальда—Волфовица: результат
Дата: 2018-12-21, просмотров: 687.