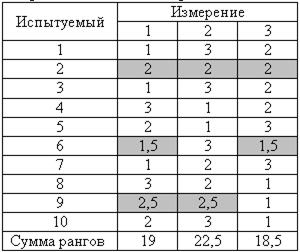
Можно ли утверждать, что существуют значимые различия между результа­тами трех измерений?

Выберем уровень значимости α =0,05 и сформулируем нулевую и альтерна­тивную гипотезы.

Н₀:: Различия между результатами проведенных измерений отсутствуют.

Н₁: Результаты проведенных измерений отличаются друг от друга (двусто­ронняя критическая область).

Из таблицы видно, что в ней есть три случая связанных рангов (выделены в таблице). Мы уже говорили, что многие непараметрические методы статисти­ки чувствительны к ситуации связанных рангов. Для их учета в расчетные формулы приходится вводить различные корректирующие поправки, услож­няющие процесс вычислений⁴.

⁴ Выше уже отмечалось, что в некоторых пособиях, где рассматриваются непараметрические методы статистики, ситуация связанных рангов игнорируется. Это приводит к несовпадению результатов, вычисленных вручную и полученных для тех же данных с помощью программы SPSS. Увы, данное обстоятельство также игнорируется [см., например: Наследов, 2006, с. 183, 184].

Расчетная формула для теста Фридмана, учитывающая наличие связанных рангов, принимает следующий вид:

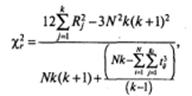
где g_i — число групп связанных рангов в каждой строке таблицы, t — размер каждой группы связанных рангов (сколько одинаковых рангов в нее входит).

Обратите внимание! Даже если в строке нет связанных рангов, в тесте Фридмана каждый отдельный (несвязанный) ранг рассматривается как группа связанных рангов, содержащая одно значение (t = 1). Например, в первой, строке таблицы 5.6 нет связанных рангов. Но в соответствии с правилами использования приведенной формулы, три отдельных ранга 1, 3, 2 рассматриваются как три группы связанных рангов размером t = 1 (содержащих одно зна­чение).

Прежде чем приступить к вычислениям, найдем значение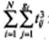

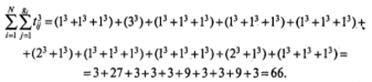
Приступим к вычислениям. Учтем, что N =10; k=3; R ₁=19; R ₂=22,5; R ₃=18,5.

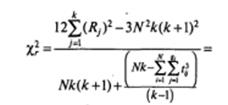
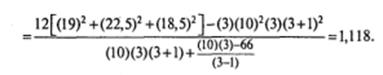
Из табл. 2 (Приложение 2) для df =( k -1)= (3—1) = 2 и уровня значимости α = 0,05 находим  Х² _{r критич} = 5,99. Поскольку значение Х² _{r эмпир} = 1,118 меньше кри­тического, нет оснований отвергнуть нулевую гипотезу. Между результатами проведенных измерений отсутствуют различия.

ВКЛЮЧАЕМ КОМПЬЮТЕР....   

Перенесем данные о пропусках занятий в переменные «Лекция 1» (lecture1), «Лек­ция 2» (lecture2) и «Лекция 3» (lecture 3). Дальнейшая последовательность действий и результат показаны на рис. 5.4—5.6. На рис. 5.7, 5.8 приведены результаты теста Фридмана для примера с мышами и случая связанных рангов.

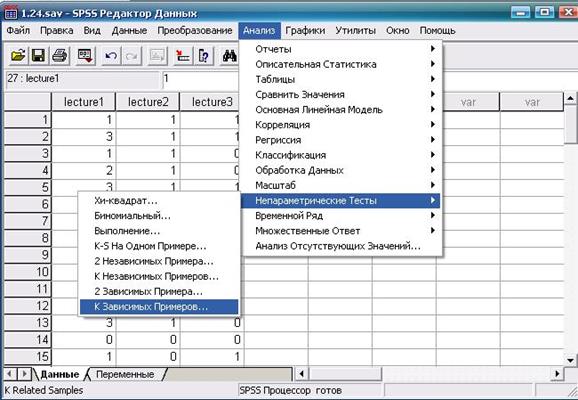
Рис. 5.4. Выбор требуемой статистической процедуры

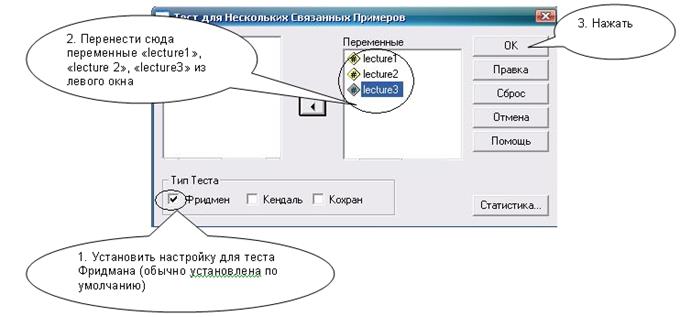
Рис. 5.5. Тест Фридмана: необходимые действия и настройки

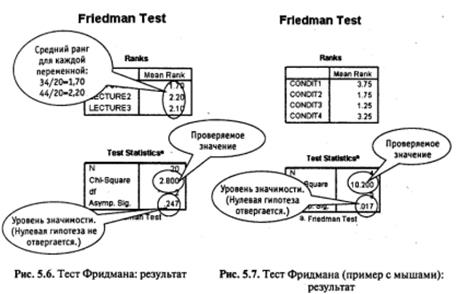
Рис. 5.8. Тест Фридмана (случай связанных рангов): результат

Этим примером мы завершаем рассмотрение ситуаций, относящихся к случаю связанных выборок.

Перейдем к следующему разделу и рассмотрим непараметрические тесты, относя­щиеся к независимым выборкам.