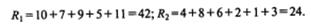
После выполнения всех подготовительных преобразований можно присту­пать к проверке статистических гипотез.

Выбираем уровень значимости α =0,05 и формулируем нулевую и альтер­нативную гипотезы.

Н₀: Значения предродовой тревожности у женщин — старших детей в семье не отличаются от значений предродовой тревожности у женщин — младших (единственных) детей в семье.

Н₁: Значения предродовой тревожности у женщин — старших детей в семье меньше значений предродовой тревожности у женщин — младших (единственных) детей в семье (односторонняя критическая область).

Для проверки нулевой гипотезы вычисляются два значения:

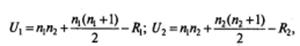
где n ₁ — объем меньшей выборки; n₂ — объем большей выборки.

Из таблицы находим n ₁ = 5; = 6; R₁ = 42; R₂ = 24. Подставляем эти значения в формулы и находим:   

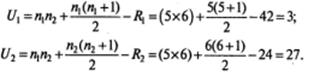
Значения U₁ и U₂ связаны между собой¹⁰:

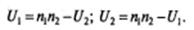
¹⁰ Строго говоря, вычисляется одно значение U, которое сравнивается со значением (n ₁ n₂)/2. Если U оказывается больше, чем (n ₁ n₂)/2, то используется другое значение U '= (n ₁ n₂) — U.

Из двух значений U₁ и U₂ выбираем меньшее U = min (U_1, U₂) = 3 и обращаемся к статистической таблице для теста Манна—Уитни. В таблице 7 (Приложение 2) приведен фрагмент такой таблицы, соответствующий рассмотренному примеру.    

В таблице приведены крайние значения вероятностей (соответствующих односторонней критической области), при которых для данных значений U, n ₁ и n₂ различия между выборками считаются случайными.

Если выбранный уровень значимости α меньше приведенного в таблице значения вероятности, то нет оснований отвергнуть нулевую гипотезу.   

Если выбранный уровень значимости α равен приведенному в таблице значению вероятности или превышает его, то нулевая гипотеза отвергается и принимается альтернативная.  

Из табл. 7 для U =3, n ₁ = 5 и n₂ = 6 находим р=0,015.

 Поскольку α = 0,05 больше, чем р = 0,015, нулевая гипотеза отвергается и принимается альтернативная. Значения предродовой тревожности у женщин — А старших детей в семье меньше значений предродовой тревожности у жен­щин — младших (единственных) детей в семье.

В случае отсутствия статистической таблицы для теста Манна—Уитни вы­числяется значение z по следующей формуле:

По таблице 1 (Приложение 2) для z -распределения находим, что левее зна­чения z = −2,191 лежит вероятность р = 0,0 14 (левосторонняя критическая об­ласть), что с учетом возможностей табл. 1 практически совпадает с полученным выше значением р =0,015. Поскольку р =0,015 меньше, чем α =0,05, нулевая гипотеза отвергается и принимается альтернативная. Значения предродовой тревожности у женщин — старших детей в семье меньше значений предродовой тревожности у женщин — младших (единственных) детей в семье.

Возможен еще один подход к определению U₁ и U₂, основанный на прямом сравнении выборок между собой и позволяющий обходиться без предваритель­ного ранжирования результатов.

Вернемся к таблице 6.8. Рассмотрим обе выборки и сравним каждое значе­ние в первой выборке с каждым значением во второй выборке. Определим, сколько значений из второй выборки больше данного значения из первой вы­борки. Например, первое значение в первой выборке — 73. Во второй выборке все 5 значений (85, 79, 82, 75, 93) больше чем 73. Результат сравнения равен 5. Запишем его в скобках рядом со значением 73 (табл. 6.11). Второе значение в первой выборке — 80. Во второй выборке три значения (85, 82, 93) больше чем 80. Результат сравнения — 3. Продолжим эту процедуру для всех значений в первой выборке.

После завершения работы с первой выборкой поменяем направление срав­нения. Сейчас каждое значение во второй выборке сравним с каждым значе­нием в первой выборке. Результаты сравнения также запишем в скобках рядом с соответствующим значением из второй выборки.

Найдем сумму результатов сравнения первой выборки со второй (U_1→2) и второй выборки с первой (U_2→1):

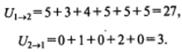
Нетрудно видеть, что полученные результаты совпадают с ранее найденны­ми значениями U₁ и U₂, из которых в тесте Манна — Уитни используется наи­меньшее:

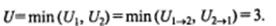
Одна из типичных ситуаций, возникающих при использовании теста Манна — Уитни, касается наличия связанных рангов. В том случае, когда в выборках имеются одинаковые значения, приходится использовать иной, более слот алгоритм действий.

Таблица 6.11