| Женщины | Количество ежедневно выкуриваемых сигарет
|
Итого
| ||||
| Не более одной | От 2 до 5 | От 6 до 10 | От 11 до 20 | Более 20 | ||
| Имеющие детей | 5 | 13 | 11 | 9 | 7 | 45 |
| Не имеющие детей | 8 | 8 | 9 | 9 | 4 | 38 |
| Итого | 13 | 21 | 20 | 18 | 11 | 83 |
Можно ли на основании полученных данных сделать вывод о том, что между женщинами, имеющими детей, и бездетными существуют различия в количестве ежедневно выкуриваемых сигарет?
В принципе, для ответа на поставленный вопрос можно использовать тест Х2, рассматривая приведенные данные как распределенные по нескольким категориям. Однако в том случае, когда полученные результаты допускают упорядочивание по возрастанию (в нашем случае — по числу выкуриваемых ежедневно сигарет) возможно применение теста Колмогорова—Смирнова для двух независимых выборок. Тест позволяет сравнивать распределение результатов в двух независимых выборках, содержащих значения, выраженные в шкале не ниже порядковой. Пример использования этого теста для случая одной выборки был рассмотрен в параграфе 3.3.
В данном случае, по аналогии с рассмотренным ранее примером, рассматриваются две эмпирические кумулятивные функции распределения (значения накопленных к данному разряду таблицы относительных частот): Sn 1 (X) для первой выборки и Sn 2 (X) для второй выборки. Вычисляются величины расхождений между ними, и находится значение D = mах│Sn 1 (X) − Sn 2 (X)│— максимальное (по модулю) значение различий между эмпирическими кумулятивными функциями распределения для первой (n 1) и второй (n2) выборки.
В таблице 6.16 показаны все необходимые вычисления для получения значения D.
Таблица 6.16
Тест Колмогорова—Смирнова для двух независимых выборок: расчетная таблица
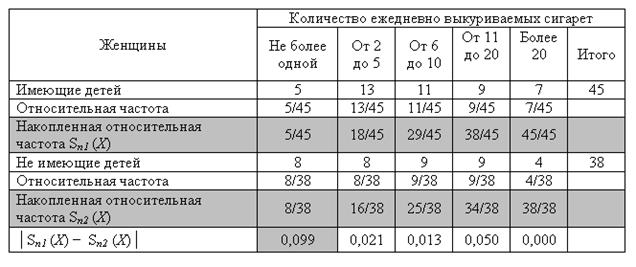
Выберем уровень значимости α =0,05 и сформулируем соответствующие гипотезы.
Н0: Нет различий в количестве ежедневно выкуриваемых сигарет у женщин,
имеющих детей, и у женщин без детей.
Н1: Существуют различия в количестве ежедневно выкуриваемых сигарет у женщин, имеющих детей, и у женщин без детей (двусторонняя критическая область14).
14 Альтернативная гипотеза не утверждает, что одни курят больше, а другие меньше.
На основании таблицы 6.16 (последняя строка) находим
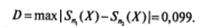
Это эмпирическое значение сравнивается с критическим, которое определяется на основе таблицы критических значений для теста Колмогорова—Смирнова для двух независимых выборок (см. табл. 9, Приложение 2, случай большой выборки и двусторонней критической области). Если эмпирическое значение D меньше критического, то нет оснований отвергнуть нулевую гипотезу. Если эмпирическое значение D больше критического или равно ему, то нулевая гипотеза отвергается и принимается альтернативная.
Из табл. 9 следует, что для уровня значимости α =0,05 критическое значение D находится по следующей формуле:
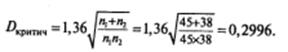
Поскольку эмпирическое значение D (0,099) меньше критического (0,2996), нет оснований отвергнуть нулевую гипотезу. Женщины, имеющие детей, курят столь же интенсивно, что и женщины без детей.
При работе с малыми выборками, в том случае, когда n1= n2 =N≤40, используется другая таблица критических значений для данного теста.
Рассмотрим еще один пример.
Социальный работник, работающий с подростками группы риска, проанализировал 30 личных дел подростков-правонарушителей из числа новых иммигрантов: 15 дел иммигрантов из бывшего СССР и 15 дел иммигрантов из Эфиопии. Его интересовало, в каком возрасте теми и другими были совершены первые правонарушения.
Полученные результаты показаны в таблице 6.17.
Таблица 6.17
Дата: 2018-12-21, просмотров: 751.