| А | В | (А+В) |
| С | D | (С+ D ) |
| (А + С) | (В+ D ) | N=А+В+С+ D |
Вероятность вычисляется по следующей формуле:
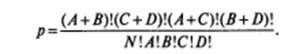
Подставим в эту формулу данные из таблицы 6.12:
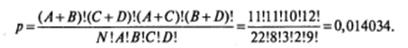
Однако для точного вычисления требуемой вероятности полученного результата недостаточно. Необходимо дополнительно рассмотреть вероятности всех теоретически возможных вариантов распределения результатов в таблице 6.5, которые носят более крайний (экстремальный) характер по сравнению с исходным.
Вернемся к нашему примеру (табл. 6.5) и представим его в следующем виде:

Более экстремальные распределения результатов, не искажающие их итогов, будут иметь такой вид:
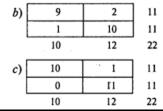
Вычислим соответствующие вероятности для случаев b) и с):
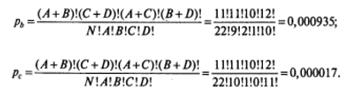
Тогда точная вероятность будет равна сумме полученных значений:
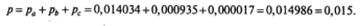
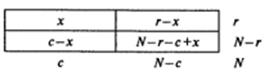
Для рассмотрения ситуации в общем виде представим распределение результатов в таблице размером (2x2) следующим образом:
Тогда, в общем случае, искомое точное значение вероятности будет определяться как сумма нескольких слагаемых, каждое из которых вычисляется по формуле:
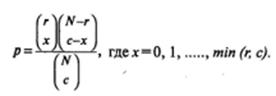
Вернемся к нашему примеру. Из таблицы 6.6 можно видеть, что x =8, r = 11, с = 10 и min (r, с) = 10.
Следовательно, вычисления по этой формуле начнутся со значения x = 8; закончатся, когда x примет значение x = min (r, с)= 10. В итоге будут получены три значения вероятности для x =8, x =9, x = 10, сумма которых даст, разумеется, тот же результат, который был получен выше. Несмотря на явные преимущества точного теста Фишера, особенно при работе с малыми выборками, он не столь популярен, как тест X2, поскольку, как видно из приведенного примера, требует большого объема дополнительных вычислений. Поэтому при наличии достаточных по размеру выборок исследователи предпочитают применять тест X2. При наличии малых выборок требуемых вычислений удается избегать за счет использования громоздкой статистической таблицы для этого теста7.
7 В книге Sidney Siegel [Siegel, 1956] статистическая таблица для точного теста Фишера занимает
15 страниц.
В таблице 10 (Приложение 2) приведен фрагмент этой таблицы, относящийся к рассматриваемому примеру.
Выберем уровень значимости α =0,05 и сформулируем соответствующие гипотезы.
Н0: Число случаев храпа одинаково для людей, спящих на спине, и для людей, спящих в других позах.
Н1: Число случаев храпа неодинаково для тех, кто спит на спине, и для тех, кто спит в других позах (двусторонняя критическая область8).
8 Поскольку в альтернативной гипотезе не утверждается, что среди тех, кто спит на спине, число случаев храпа больше.
Если все необходимые для проверки вычисления осуществляются вручную (как показано выше), то получаемое в итоге точное значение вероятности р (в нашем случае р =0,015) сравнивается со значением выбранного уровня значимости α для случая односторонней критической области. Если р > α, нет оснований отвергнуть нулевую гипотезу. Если р < α, то нулевая гипотеза отклоняется и принимается альтернативная.
В нашем случае р=0,015. Для перехода к двусторонней критической области удвоим это значение. Получим р=0,030. Поскольку это значение меньше, чем α =0,05, нулевая гипотеза отклоняется и принимается альтернативная. Число случаев храпа неодинаково для тех, кто спит на спине, и для тех, кто спит в других позах.
 В случае использования статистической таблицы для точного теста Фишера последовательность действий такова:
В случае использования статистической таблицы для точного теста Фишера последовательность действий такова:
Находим в таблице 10 (Приложение 2) случай, соответствующий значениям (А+В) = 11 и (С+ D) = 11. В колонке «В (или А)» ищем значение В, соответствующее тому, что приведено в таблице 6.6 (В =3). Поскольку этого значения в таблице нет, используем вместо В значение А = 8. Напротив значений В (или А) в таблице приведены критические значения D (или С), соответствующие указанным уровням значимости для односторонней критической области. Поскольку в рассматриваемом примере используется двусторонняя критическая область и уровень значимости α =0,05, то в таблице необходимо искать значения, соответствующие α =0,025.
Если фактическое значение D (или С), приведенное в таблице 6.6, больше критического значения D (или С), приведенного в табл. 10, нет оснований отвергнуть нулевую гипотезу. Если фактическое значение D (или С) меньше или равно критическому значению D (или С), нулевая гипотеза отвергается и принимается альтернативная.
Из таблицы следует, что для уровня значимости α =0,025 и А = 8 критическое значение С=2. Фактическое значение С также равно двум (табл. 6.6).
Поскольку эмпирическое значение (С=2) равно критическому, нулевая гипотеза отвергается и принимается альтернативная (для α =0,05): число случаев храпа неодинаково для тех, кто спит на спине, и для тех, кто спит в других позах.
При работе с большими выборками обычно используется другой подход, основанный на свойствах нормального распределения. Вначале вычисляет значение z по следующей формуле (смысл входящих в формулу обозначений рассмотрен выше):
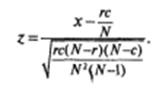
Затем по таблице z -распределения определяется соответствующая полученному значению z вероятность, которая сравнивается с выбранным уровнен значимости α для односторонней критической области.
ВКЛЮЧАЕМ КОМПЬЮТЕР...
Создадим в программе SPSS переменные «Храп» (snoring) (1 — есть храп, 2 — не храпа) и переменную «Поза во время сна» (pos), где 1 означает сон на боку или животе, 2 — сон на спине.
Дальнейшие действия и результат показаны на рис. 6.6—6.8.

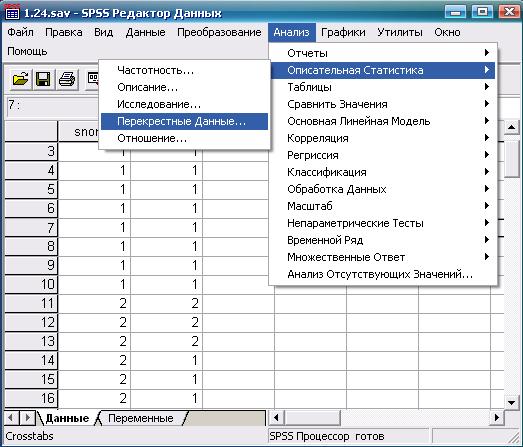
Рис. 6.6. Выбор требуемой статистической процедуры



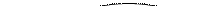



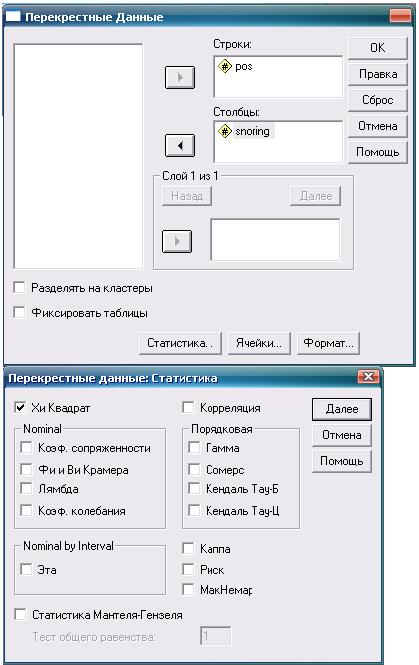
Рис. 6.7. Точный тест Фишера: необходимые действия и настройки

Рис. 6.8. Точный тест Фишера: результат
Дата: 2018-12-21, просмотров: 728.