| Возраст первого правонарушения
| |||||||
| 12 | 13 | 14 | 15 | 16 | 17 | Итого | |
| Подростки из б. СССР | 0 | 2 | 1 | 3 | 6 | 3 | 15 |
| Подростки из Эфиопии | 1 | 4 | 3 | 2 | 5 | 0 | 15 |
| Итого | 1 | 6 | 4 | 5 | 11 | 3 | 30 |
Можно ли утверждать, что между двумя выборками существуют различия в возрасте первых правонарушений?
Выберем уровень значимости α =0,05 и сформулируем нулевую и альтернативную гипотезы.
Н0:: Между подростками-иммигрантами из бывшего СССР и подростками-иммигрантами из Эфиопии отсутствуют различия в возрасте первых правонарушений.
Н1: Между подростками-иммигрантами из бывшего СССР и подростками-иммигрантами из Эфиопии существуют различия в возрасте первых правонарушений (двусторонняя критическая область).
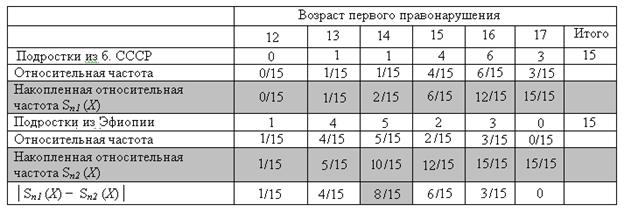
Как и в предыдущем примере, создадим расчетную таблицу (табл. 6.18) и вычислим значение
D = mах│Sn 1 (X) − Sn 2 (X)│, где n1= n2= N=15.
Как видно из таблицы, D = mах│Sn 1 (X) − Sn 2 (X)│=8/15=0,533.
Запишем полученный результат следующим образом:
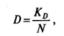
где К D — числитель дроби, соответствующий значению D (в нашем случае К D =8), N= n1= n2= 15.
В таблице 8 (Приложение 2, случай малой выборки) для каждого значения N (от 3 до 40) приведены критические значения К D для односторонней и двусторонней критических областей и соответствующих значений уровня значимости α.
Таблица 6.18
Расчетная таблица
Если эмпирическое значение К D меньше приведенного в таблице, нет оснований отвергать нулевую гипотезу. Если эмпирическое значение К D больше или равно приведенному в таблице, нулевая гипотеза отвергается и принимается альтернативная.
Для двусторонней критической области с уровнем значимости α =0,05 и N= 15, критическое значение К D=8. Поскольку это совпадает со значение К D полученным на основе таблицы 6.18, нулевая гипотеза отвергается. Подростки из бывшего СССР и из Эфиопии начинают совершать первые правонарушения в различном возрасте.

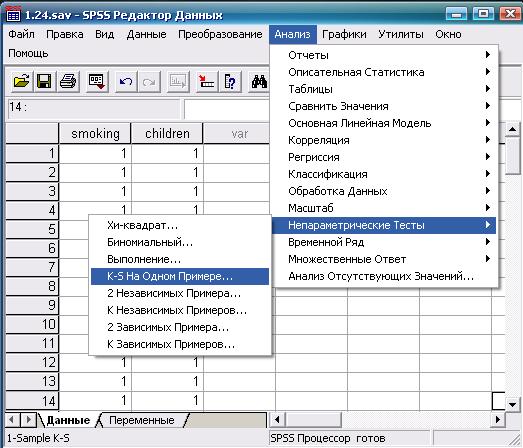
Рис. 6.13. Выбор требуемой статистической процедуры
ВКЛЮЧАЕМ КОМПЬЮТЕР…
В переменной «Курение» (smoking) цифрами от 1 до 5 обозначим число ежедневно выкуриваемых сигарет (в соответствии с градациями, приведенными в таблице 6 14). В переменной «Дети» (children) 0 означает отсутствие детей, 1 - их наличие. Дальнейшая последовательность действий и конечный результат показаны на рис. 6.13-6.15.

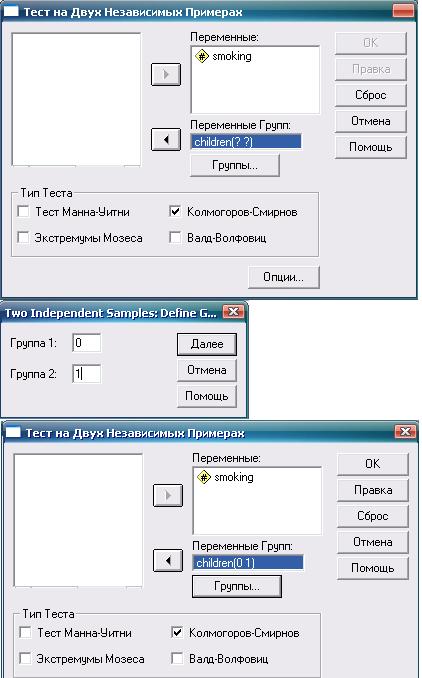
Рис. 6.14. Тест Колмогорова—Смирнова для двух независимых выборок: необходимые действия и настройки
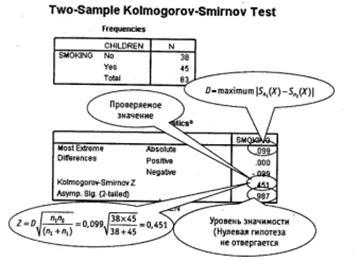
Рис. 6.15. Тест Колмогорова—Смирнова для двух независимых выборок: результат (смысл обозначений см. в параграфе 6.4)
Для второго примера (возраст первого правонарушения) создадим переменные «Возраст» (age) и «Происхождение» (origin), в которой 0 будет обозначать подростков из бывшего СССР, а 1 — подростков из Эфиопии. Итоговый результат показан на рис. 6.16.

Рис. 6.16. Тест Колмогорова—Смирнова для двух независимых результатов (пример с правонарушителями)
Дата: 2018-12-21, просмотров: 755.