| Уроженки Израиля | Иммигрантки | Итого | |
| Блондинки | 20 | 18 | 38 |
| Неблондинки | 38 | 14 | 52 |
| Итого | 58 | 32 | 90 |
Можно ли на основании полученных результатов утверждать, что среди иммигранток блондинки встречаются чаще?
Для ответа на поставленный вопрос чаще всего используется тест Х2 — один из наиболее популярных непараметрических тестов. С ним мы уже встречались, когда рассматривали случай одной выборки (параграф 3.2). Тогда он применялся для сравнения эмпирического распределения качественных признаков (страна-производитель автомобилей) с теоретическим распределением (равномерным).
Гораздо чаще данный тест используется для сравнения между собой двух и более эмпирических распределений качественных признаков, полученных на независимых выборках.
В нашем примере мы имеем две независимые выборки: коренные израильтянки и иммигрантки и качественный признак — цвет волос, выраженный в дихотомической шкале наименований (блондинка или неблондинка). При этом как число независимых выборок, так и число градаций качественной переменной может быть сколь угодно большим.
Основная идея использования теста Х2 связана со сравнением наблюдаемых (observed) частот в каждой из клеток таблицы с теоретически ожидаемыми (expected) частотами. С опорой на имеющиеся наблюдаемые значения (О) и вычисленные для каждой клетки таблицы ожидаемые значения (Е) определяется значение Х2.
Для таблицы, содержащей r строк и k столбцов, формула для вычисления Х2 выглядит так:
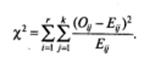
Для понимания смысла формулы представим расчетную таблицу следующим образом (табл. 6.2).
Таблица 6.2
Таблица для теста Х2 (случай двух независимых выборок)
| Выборка 1 | Выборка 2 | Итого | |
| Категория 1 | А (O11) (Е11) | В (O12) (Е12) | (А+В) |
| Категория 2 | С (O21) (Е21) | D (O22) (Е22) | (С+ D) |
| Итого | n1=(А+С) | n2=(В+D) | N=n1+n2 |
Ожидаемые (теоретические) частоты вычисляются так:
Е11=(А+В)(А+С)/ N
Е12=(А+В)(В+ D)/ N
Е21=(С+ D)(А+С)/ N
Е22=(С+ D)(В+ D)/ N
Если эти выражения подставить в формулу для Х2, то после несложных алгебраических преобразований получим следующий результат (справедливый только для таблицы размером 2x2):
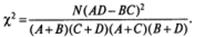
Подставим в выражение для Х2 значения, полученные Антоном и Ричардом (N=90; А=20; В= 18; С=38; D= 14), и произведем необходимые вычисления:
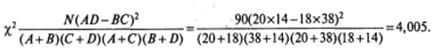
Корректнее пользоваться другой формулой, в которую введена поправка на непрерывность3 для таблиц размером 2x2:
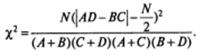
3 С поправкой на непрерывность для таблицы размером 2х2 мы уже сталкивались при рассмотрении теста МакНемара. Она позволяет корректировать ошибки, возникающие при использовании непрерывного распределения Х2 для анализа дискретных данных. Если эту поправку не использовать, то значение Х2 оказывается большим, чем в том случае, если эта поправка используется. При проверке статистических гипотез это увеличивает число случаев, при которых нулевая гипотеза отвергается без должных на то оснований. К сожалению, во многих случаях исследователи поправку на непрерывность игнорируют и производят вычисления без нее.
После всех предварительных замечаний и преобразований приступим к формулированию нулевой и альтернативной гипотез (как и прежде, используем уровень значимости α =0,05).
Н0: Среди коренных израильтянок и среди иммигранток девушки-блондинки встречаются одинаково часто.
Н1: Среди девушек-иммигранток блондинки встречаются чаще, чем среди коренных израильтянок (односторонняя критическая область).
Для проверки нулевой гипотезы вычисляется эмпирическое значение Х2эмпир по приведенной выше формуле (с поправкой на непрерывность). Подставим в эту формулу значения, полученные Антоном и Ричардом: N=90, А=20; В= 18; С=38; D=14
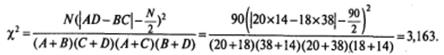
Полученное значение Х2эмпир сравниваем со значением Х2критич, которое находим в табл. 2 (Приложение 2) для выбранного уровня значимости α и числа степеней свободы df =( r -1)( k -1), где r — число строк в расчетной таблице, а k — число столбцов в ней. В нашем случае r = k =2 и df =1.
В табл. 2 приведены значения Х2критич для различных значений уровня значимости α, соответствующих двусторонней критической области. Как мы уже знаем, односторонней критической области с уровнем значимости α соответствует двусторонняя критическая область с уровнем значимости 2α. В нашем случае α =0,05. Поэтому ищем в таблице значение Х2критич для df =1 и уровня значимости 2α=0,1. Найденное значение Х2критич =2,71.
Поскольку Х2эмпир > Х2критич, нулевая гипотеза отвергается и принимается альтернативная. Девушки-блондинки встречаются чаще среди иммигрантов, чем среди коренных израильтянок4.
4 Использование односторонней критической области, позволяющей определить направление различий между двумя выборками, возможно только для таблицы размером 2x2. Во всех остальных случаях использования теста х2 это сделать невозможно.
С таблицей размером 2x2 связан еще один показатель, называемый отношением шансов (odds ratio— О R).
На основании результатов, полученных Антоном и Ричардом, можно сказать, что шанс встретить блондинку среди иммигранток определяется как 18:14. Шанс встретить блондинку среди коренных израильтянок будет 20:38.
Оdds Ratio показывает отношение полученных результатов (отношение шансов):
О R = 18:14/20:38 = 2,44.
Иными словами, шанс встретить блондинку среди студенток-иммигранток в 2,44 раза выше шанса встретить блондинку среди студенток, родившихся в Израиле5.
5 Нетрудно видеть из таблицы 6.2, что О R определяется как ВС/А D.
Приведем еще один пример для случая, когда результаты представлены в шкале наименований, содержащей более двух категорий.
В ходе одного из исследований, проведенных центром RADAR, были получены социодемографические характеристики израильских героиновых наркоманов [Isralowitz et al., 2007]. В частности, были получены данные об их семейном положении и типичной занятости в течение последних трех лет. Это позволило сформировать две независимые выборки, первая из которых включила тех, кто на протяжении трех последних лет имел полную или частичную занятость, а вторая тех, кто в течение последних трех лет был безработным.
В таблице 6.3 приведены данные о семейном положении для каждой из выборок (данные только для мужчин).
Таблица 6.3
Дата: 2018-12-21, просмотров: 699.