|
Респондент
| Стиль интервью
| L | L2 | ||
| А | В | С | |||
| 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 1 | 1 | 0 | 2 | 4 |
| 3 | 0 | 1 | 0 | 1 | 1 |
| 4 | 0 | 0 | 0 | 0 | '0 |
| 5 | 1 | 0 | 0 | 1 | 1 |
| 6 | 1 | 1 | 1 | 3 | 9 |
| 7 | 1 | 1 | 0 | 2 | 4 |
| 8 | 0 | 1 | 1 | 2 | 4 |
| 9 | 1 | 0 | 0 | 1 | 1 |
| 10 | 0 | 0 | 1 | 1 | 1 |
| 11 | 1 | 1 | 0 | 2 | 4 |
| 12 | 1 | 1 | 0 | 2 | 4 |
| 13 | 1 | 1 | 0 | 2 | 4 |
| 14 | 0 | 0 | 0 | 0 | 0 |
| 15 | 1 | 0 | 1 | 2 | 4 |
| 16 | 0 | 1 | 1 | 2 | 4 |
| 17 | 1 | 0 | 0 | 1 | 1 |
| 18 | 1 | 1 | 0 | 2 | 4 |
| 19 | 0 | 1 | 0 | 1 | 1 |
| 20 | 1 | 0 | 1 | 2 | 4 |
| ∑G=29 | G1 = 12 | G2=11 | G3 = 6 | ∑L = 29 | ∑L2 = 55 |
| G21 = 144 | G22= 121 | G23 = 36 | |||
 Ответ на поставленный вопрос может быть получен с помощью теста Кохрана. Данный тест является развитием теста МакНемара (см. параграф 4.1) и предназначен для сравнения результатов более чем двух измерений, произведенных на одной выборке в различное время или в различных условиях1.
Ответ на поставленный вопрос может быть получен с помощью теста Кохрана. Данный тест является развитием теста МакНемара (см. параграф 4.1) и предназначен для сравнения результатов более чем двух измерений, произведенных на одной выборке в различное время или в различных условиях1.
1 Возможен иной подход к работе с зависимыми выборками. Как известно, выборки считаются зависимыми, если каждому значению из одной выборки можно поставить в соответствие единственное значение из другой выборки. Так, в рамках одного из исследований было сформировано несколько однородных выборок по 3 человека в каждой. Каждый из участников в каждой выборке получил предназначенную только для него информацию (позитивную, негативную, нейтральную) об одном из законов, который планировался к принятию. Затем выяснялось отношение к этому закону (за или против) и проверялось наличие различий в результатах для тех, кто в каждой выборке получил соответствующую информацию (то есть сравнивались результаты тех, кто в каждой из выборок получил только позитивную, только негативную или только нейтральную информацию об этом законе) [по: Runyon, 1977].
В тесте Кохрана, как и в тесте МакНемара, используются дихотомические данные типа «да» — «нет», либо данные, допускающие дихотомическую категоризацию (для теста МакНемара рассматривался пример с дихотомической категоризацией предродовой тревожности: «предродовая тревожность высокая» — «предродовая тревожность низкая»).
Если результаты каждого измерения носят случайный характер, то числа успешных и неуспешных обращений к респондентам в каждом, дом из столбцов таблицы не должны значительным образом отличаться друг от друга. Аналогичным образом можно предположить, что если изменение стиля общения не оказывает своего влияния на результаты, их распределение по горизонтали также должно носит случайный характер.
Кохран предложил специальную расчетную формулу, позволяющую одновременно оценивать случайный характер результатов как по столбцам, так и по строкам таблицы, и показал, что для проверки статистических гипотез можно использовать статистическую таблицу для теста Х2.
Проверка осуществляется по отношению к результатам, которые можно условно считать «успешными». В нашем случае это число случаев, когда респондент дал согласие на участие в опросе. Такие случаи отмечены в таблице как«1»2.
2 Выбор результата, считаемого «успешным», является условным. Результаты проверки не изменятся, если все необходимые вычисления будут проделаны для результатов, обозначенных как «0».
Сделаем ряд необходимых дополнений в таблицу 5.1.
1. Внизу каждого столбца запишем количество «успехов» (то есть единиц и обозначим их символом G.
2. Найдем сумму всех «успехов» и обозначим ее ∑G.
3. Вычислим для каждого столбца значение G2.
4. Найдем количество «успехов» по строкам, обозначив их как L.
5. Для каждой строки найдем значение L2.
6. Определим сумму L и L2.
Нами проделана вся подготовительная работа. Можно приступать к проверке гипотез.
Итак, выбираем уровень значимости а=0,05 и формулируем нулевую и альтернативную гипотезы.
Н0: Вероятность согласия респондента на проведение опроса одинакова для всех стилей общения с ним.
Н1: Вероятность согласия респондента на проведение опроса различна для различных стилей общения с ним (двусторонняя критическая область).
Для принятия решения вычисляется значение Q по следующей формуле:
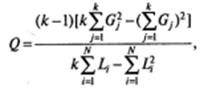
где N — число строк в расчетной таблице (размер выборки; в нашем случае N=20); k — число столбцов в расчетной таблице (число измерений, проведенных на выборке; в нашем случае k = 3).
Подставим в формулу необходимые значения из таблицы 5.1:
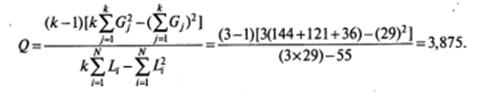
Полученное значение Qэмпир сравниваем с критическим значением Х2критич, которое находится в таблице критических значений теста Х2 для выбранного уровня значимости α и числа степеней свободы df =(k -1). Если Qэмпир меньше Х2критич,. нет оснований отклонить нулевую гипотезу. Если Qэмпир больше или равно Х2критич, нулевая гипотеза отклоняется и принимается альтернативная.
В нашем случае α =0,05, df =(3-1) = 2. В табл. 2 (Приложение 2) находим Х2критич =5,99
Поскольку Qэмпир =3,875 меньше Х2критич = 5,99, нет оснований отклонить нулевую гипотезу. Готовность респондента принять участие в опросе не определяется стилем общения с ним. Возможно, более действенным фактором будет время проведения опросов.
ВКЛЮЧАЕМ КОМПЬЮТЕР...
Сведения об эффективности каждого из стилей представлены в переменных «Стиль 1 » (style), «Стиль 2» (style) и «Стиль 3» (style). .
Дальнейшая последовательность действий, включая результат, показана на рис. 5.1-5.3.

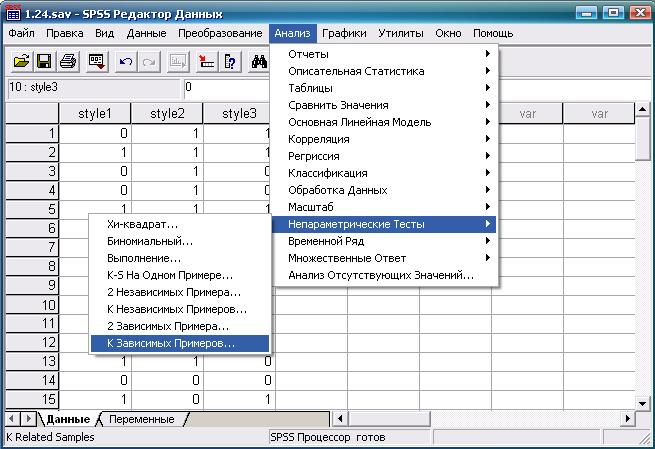
Рис. 5.1. Выбор требуемой статистической процедуры
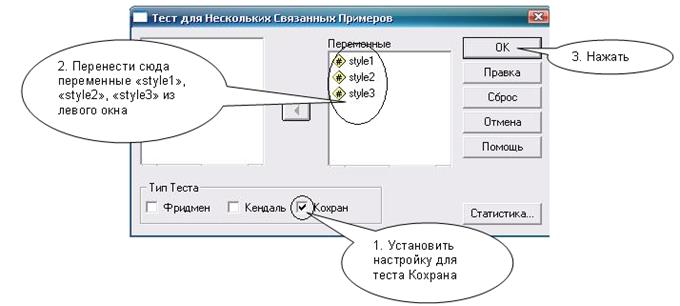

Рис. 5.2. Тест Кохрана: необходимые действия и настройки
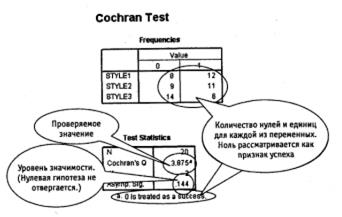
Рис. 5.3. Тест Кохрана: результат
СТУДЕНТЫ ГОЛОСУЮТ НОГАМИ, ИЛИ ТЕСТ ФРИДМАНА
Уже знакомый нам преподаватель предположил, что одни занятия студенты прогуливают чаще, а другие — реже. Он связался с другими преподавателями и в конце семестра получил данные о числе пропусков занятий у студентов своей группы еще по двум предметам; Полученные результаты приведены в таблице 5.2. Таблица содержит сведения о числе пропусков занятий для студентов одной группы по трем предметам: А, В, С.
Можно ли на основании полученных данных утверждать, что студенты пропускают занятия выборочно, в зависимости от изучаемого предмета?
Ответ на этот вопрос может быть получен несколькими путями. Первый путь связан с попарным сравнением числа пропусков по предметам А, В, С между собой. Для этого потребуется трижды использовать, например, тест Вилкоксона.
Существует другая возможность, предложенная Фридманом. Тест Фридмана позволяет сравнивать результаты трех и более измерений, полученных на одной и той же выборке. С его помощью можно определить, отличаются ли полученные результаты друг от друга, без выявления направления отличий3.
3 В общем случае тест Фридмана рассматривается как непараметрический аналог двухфакторного дисперсионного анализа (Two-way ANOVA by ranks). Он позволяет оценить эффект воздействия двух факторов на измеряемую величину. В нашем примере измеряемая величина — число пропусков занятий. Она находится под воздействием двух факторов. Первый фактор - «предметы/ преподаватели», имеющий три уровня. Второй фактор - «студенты», имеющий 20 уровней.
Таблица 5.2
Число пропусков занятий по предметам А, В и С
| Студент
|
Предметы
| Студент
| Предметы
| ||||
| А | В | С | А | В | С | ||
| 1 | 3 | 5 | 7 | 11 | 2 | 4 | 1 |
| 2 | 5 | 2 | 3 | 12 | 2 | 0 | 3 |
| 3 | 2 | 6 | 4 | 13 | 5 | 3 | 0 |
| 4 | 6 | 7 | 5 | 14 | 0 | 3 | 3 |
| 5 | 7 | 1 | 3 | 15 | 3 | 7 | 5 |
| 6 | 5 | 0 | 2 | 16 | 0 | 5 | 4 |
| 7 | 0 | 4 | 3 | 17 | 3 | 4 | 6 |
| 8 | 4 | 5 | 6 | 18 | 1 | 6 | 4 |
| 9 | 1 | 2 | 3 | 19 | 3 | 5 | 3 |
| 10 | 5 | 7 | 7 | 20 | 5 | 1 | 2 |
Тест Фридмана, как и тест Вилкоксона, также использует процедуру ранжирования результатов измерений, но ранжирование происходит не по вертикали, как в тесте Вилкоксона, а по горизонтали, от измерения к измерению. Например, первый студент по предмету А пропустил 3 занятия, по предмету В — 5 занятий, по предмету С — 7 занятий. Если эти результаты проранжировать, то получим ранги 1, 2, 3 (первый ранг приписывается наименьшему значению).
Перепишем таблицу 5.2 с указанием рангов для каждого студента. Получим таблицу 5.3, в которой выделены значения рангов для каждого студента.
Если предположить, что число пропусков мало меняется от предмета к предмету, то суммы рангов для каждого из столбцов также должны мало отличаться друг от друга. В том случае, если одни предметы пропускаются чаще, а другие реже, суммы рангов в каждом из столбцов будут существенно отличаться друг от друга.
Мерой отличия сумм рангов друг от друга является значение Х2 r, вычисляемое по следующей формуле:
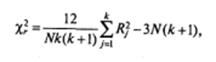
где N — число строк в таблице (размер выборки); k — число столбцов в таблице (количество измерений); Rj — сумма рангов, соответственно, для первого, второго и третьего столбцов.
Таблица 5.3
Число пропусков занятий по предметам А, В, С и их ранги
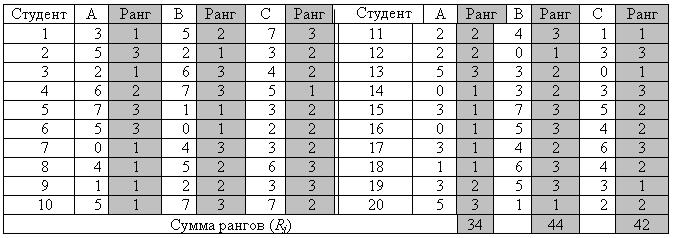
Найденное значение Х2 r эмпир сравнивается с критическим значением Х2 r критич , которое находится по уже знакомой таблице для теста Х2(табл. 2, Приложение 2) для выбранного уровня значимости а и числа степеней свободы df =( k -1).
В том случае, если Х2 r эмпир меньше Х2 r критич. нет оснований, чтобы отвергнуть нулевую гипотезу.
В том случае, Х2 r эмпир больше или равно Х2 r критич, нулевая гипотеза отвергается и принимается альтернативная.
Итак, выбираем уровень значимости α = 0,05 и формулируем нулевую и альтернативную гипотезы.
Н0: Пропуски студентами занятий носят случайный характер и не определяются изучаемым предметом.
Н1: Пропуски студентами занятий носят неслучайный характер и определяются тем, какой предмет они изучают (двусторонняя критическая область).
По данным таблицы 5.3, имеем:
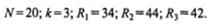
Подставляем эти значения в формулу для вычисления Х2 r:
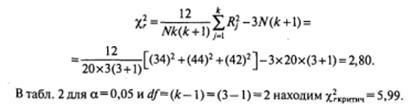
Так как Х2 r эмпир = 2,80 меньше Х2 r критич = 5,99, нет оснований, чтобы отвергнуть нулевую гипотезу. Пропуски студентами занятий носят случайный характер и не определяются изучаемым предметом.
Сейчас еще один пример.
В ходе одного из экспериментов по когнитивной психологии фиксировалось время (в минутах), которое требуется лабораторной мыши для выхода из лабиринта в четырех различных экспериментальных условиях.
Для группы из четырех мышей были получены следующие значения времени в зависимости от экспериментальных условий А, В, С, D (табл. 5.4).
Таблица 5.4
Дата: 2018-12-21, просмотров: 731.
 Предметы
Предметы