Участник	Вес «до»	Вес «после»	Участник	Вес «до»	Вес «после»
1	110	100	11	85	87 ———————— и
2	105	100	12	94	96
3	97	90	13	112	100
4	90	93	14	90	90
5	97	92	15	88	80
6	102	92	16	92	88
7	98	90	17	93	87
8	89	94	18	93	85
9	104	97	19	99	90
10	92	88	20	102	91

В том случае, когда важно не только выявить факт изменения результатов «после» по сравнению с результатами «до», но и оценить степень выражение этого изменения, используется один из популярных непараметрических тестов — тест Вилкоксона.

Для его применения необходимо соблюдение тех же условий, что и теста знаков: одна и та же выборка, для которой интересующий нас показатель измерен, как минимум, дважды — до какого-либо (экспериментального) воздействия и после него. Кроме этого, желательно, чтобы диапазон изменений результатов был достаточно широким. Например, в популярном опросе качества жизни EQ-5D[Rabin, de Charro, 2001] используется шкала, содержащая всего три значения. Очевидно, что диапазон возможных различий между результатами измерений для такой шкалы будет минимальным. В подобном случаях целесообразнее пользоваться тестом знаков.

В тесте Вилкоксона решение об отсутствии или наличии значимых различий между двумя связанными выборками принимается не на основе сравнения результатов в обеих выборках, а на основе сравнения рангов этих результатов.

Процедуру ранжирования мы подробно рассматривали в параграфе 2.3. Применим полученные знания для данного случая и, дополнив таблицу 4.5 новыми колонками, получим таблицу 4.6.

Таблица 4.6

Расчетная таблица для теста Вилкоксона

Во-первых, определим разность между результатами «после» и результатами «до» и запишем ее с учетом знака в дополнительную, четвертую, колонку таб­лицы.

Во-вторых, как и в предыдущем случае, определим направление типичного и нетипичного сдвига. Поскольку большинство значений в дополнительной колонке отрицательно, типичный сдвиг отрицательный (у большинства участ­ников эксперимента вес уменьшился), а нетипичный — положительный (у че­тырех человек из 20 вес за три месяца диеты увеличился). В таблице 4.5. случаи нетипичного сдвига выделены.

В-третьих, в новый столбец еще раз запишем значения разностей между Результатами «после» и результатами «до», но взятых по модулю (то есть без учета знака).

После этого наступает самый ответственный этап. Данные, записанные в пятом столбце, необходимо проранжировать от минимального значения до максимального. При наличии нулевых сдвигов (вес не изменился) они исключаются из жирования. В нашем случае имеется один ну­левой сдвиг (выборка уменьшится на одно значение: n = 19).

Вся подготовительная работа для использования теста Вилкоксона завершена.

Выберем уровень значимости α =0,05 и сформулируем нулевую и альтернативную гипотезы.

Н₀: После диеты изменение веса в сторону уменьшения не отличается изменения веса в сторону его увеличения (иными словами, снижение веса; одних участников эксперимента компенсируется увеличением веса у других участников).

Н₁: После диеты изменение веса в сторону его уменьшения превышает изменение веса в сторону его увеличения (то есть после диеты снижение веса; тех, кто похудел, превышает увеличение веса у тех, кто потолстел).

Как видно из формулировки альтернативной гипотезы, для проверки будет использована односторонняя критическая область.

Логика проверки достаточно проста. Если диеты не оказывают своего влияния, то после окончания эксперимента распределение результатов с точкой зрения того, что произошло с весом (насколько он уменьшился или увеличился), должно носить случайный характер. Тогда сумма рангов для результатов, говорящих о сдвиге веса в одну сторону, не должна отличаться от суммы ранг для результатов, говорящих о сдвиге веса в другую сторону.

Например, из четырех участников эксперимента двое похудели на 5 кг, а двое потолстели на 5 кг.   

Эффект от диеты (изменение веса по модулю) будет выглядеть следующий образом:

5,5,5,5.

Поскольку изменение веса одно и то же для всех участников эксперимента,  все четыре значения получат одинаковый ранг, равный 2,5:

2,5; 2,5; 2,5; 2,5.

Сумма рангов для тех, кто похудел, будет (2,5 + 2,5) = 5. Для тех, кто потолстел, получим тот же результат.

Но если представить, что после диеты два человека потолстели на 5 кг каждый, а двое похудели на 10 кг каждый, то получим другую последовательное результатов влияния диеты (по модулю):

5, 5, 10, 10.

Если эту последовательность проранжировать, получим следующий ранго­вый ряд:

1,5; 1,5; 3,5; 3,5.

Сумма рангов для тех, кто похудел, будет равна (3,5 + 3,5) = 7. Для тех, кто потолстел, —           (1,5 + 1,5) = 3. Поскольку 7 > 3, то сдвиг в сторону снижения веса более интенсивен, чем в сторону увеличения.

Найдем сумму рангов для четырех значений нетипичного (положительного) сдвига (выделено в таблице):

Т₁=3+7+1,5+1,5=13

Найдем сумму рангов для пятнадцати значений типичного (отрицательного)

сдвига:

Т₂= 16,5 + 7+ 10,5 + 7 + 16,5 + 13 + 10,5+4,5 + 19+ 13 + 4,5 + 9 + 13 + 15 + 18 = 177.

В качестве Т_эмпир используется меньшее из двух значений Т₁ и Т₂. В нашем случае Т_эмпир = 13.

 Существует статистическая таблица для теста Вилкоксона (табл. 5, Прило­жение 2), содержащая нижние (минимальные) значения Т_критич (в зависимости от размера выборки и значения а), при которых различия между типичным и нетипичным сдвигами еще могут считаться случайными. Если наблюдаемое значение Т_эмпир больше Т_критич, нет оснований для того, чтобы отклонить нуле­вую гипотезу. Если Т_эмпир меньше или равно Т_критич, нулевая гипотеза отклоня­ется и принимается альтернативная⁴.

⁴ В данном случае мы имеем нечастую ситуацию, когда правило принятия решения после сравнения Т_эмпир и Т_критич носит «обратный» характер: нулевая гипотеза отвергается, когда Т_эмпир меньше Т_критич.

Для наших результатов (Т_эмпир =13, n = 19, α =0,05) находим в таблице 5 зна­чение Т_критич = 53.

Поскольку Т_эмпир меньше Т_критич, нулевая гипотеза отвергается и принимается альтернативная гипотеза: после трех месяцев диеты у большинства участ­ников эксперимента произошло существенное снижение веса⁵.

⁵ К сожалению, полученный результат не дает ответа на вопрос, вынесенный в название данного параграфа. Несмотря на снижение веса после диеты, у нас нет оснований утверждать, что снижение веса произошло вследствие диеты. Здесь возможно действие ряда других неучтенных факторов, влияющих на вес, о которых мы ничего не знаем. Например, одновременно с диетой участники эксперимента начали заниматься спортом или вести более здоровый образ жизни (бросили курить, употреблять спиртные напитки и др.). Аналогичная ситуация в рассмотренном выше примере о пропуске занятий. Несмотря на то, что во втором семестре пропусков стало меньше, неясно, произошло ли это вследствие обещаний преподавателя добавить несколько баллов к оценке за экзамен или по другим причинам. Эти вопросы относятся к области плани­рования эксперимента, обсуждать которые у нас нет возможности.

Из табл. 5 видно, что она предназначена для выборки не более 25 человек.

 В случае больших выборок приходится прибегать к вычислению z (см. ниже) и использовать таблицу для z -распределения (табл. 1, Приложение 2). В том случае, если по каким-либо причинам нет возможности применять статистическую таблицу для теста Вилкоксона, можно сразу переходить к вычислению z независимо от размеров выборки.

ВКЛЮЧАЕМ КОМПЬЮТЕР...

В программе SPSS на основе полученных из расчетной таблицы сведений о Т₁ и Т₂ вычисляется значение z по следующей формуле:

где min (Т_1, Т₂) — минимальное из двух значений Т₁ и Т₂ ; n — объем выборки после исключения из нее нулевых сдвигов. Подставим в эту формулу наши значения min (Т_1, Т₂) = 13; n =19.

Из таблицы 1 (Приложение 2) можно найти, что этому значению z соответствует вероятность     р=0,0005.

Переходим к программе SPSS.

Переменные «w_before» и «w_after» содержат сведения о весе испытуемых до и после диеты. Дальнейшая последовательность действий (включая получаемый результат) необходимая для использования теста Вилкоксона, показана на рис. 4.7—4.9.

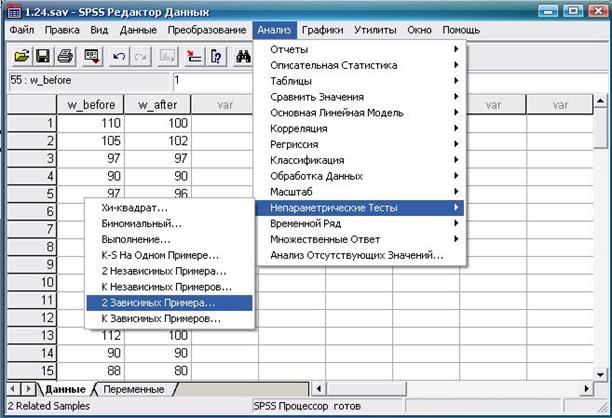
Рис. 4.7. Выбор требуемой статистической процедуры

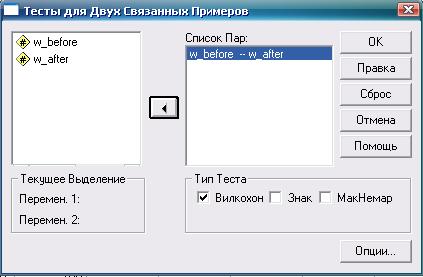
Рис. 4.8. Тест Вилкоксона: необходимые действия и настройки

Рис. 4.9. Тест Вилкоксона: результат

При работе со связанными выборками может возникнуть необходимость сравнения более чем двух выборок. В принципе, эту задачу можно решать путем последова­тельного сравнения выборок между собой. Например, при наличии трех связанных выборок вначале сравнить первую выборку со второй, потом первую с третьей, потом вторую с третьей. Нетрудно видеть, что при возрастании числа независимых выборок такой путь ведет к увеличению числа однообразных проверок.

В непараметрической статистике существует ряд методов, позволяющих анализи­ровать несколько связанных выборок, не прибегая к процедуре их попарного срав­нения.