| Студент | Число пропусков в семестре А | Число пропусков в семестре В | Студент | Число пропусков в семестре А | Число пропус- ков в семестре В |
| 3 | 3 | 11 | 0 | 2 | |
| 2 | 7 | 5 | 12 | 3 | 2 |
| 3 | 5 | 2 | 13 | 5 | 5 |
| 4 | 8 | 6 | 14 | 0 | 0 |
| 5 | 6 | 7 | 15 | 6 | 3 |
| 6 | 4 | 5 | 16 | 5 | 0 |
| 7 | 5 | 0 | 17 | 6 | 3 |
| 8 | 7 | 4 | 18 | 0 | 1 |
| 9 | 2 | 1 | 19 | 4 | 3 |
| 10 | 5 | 5 | 20 | 7 | 5 |
В данном случае одним из тестов, который можно использовать для поиска ответа на поставленный вопрос, является тест знаков. Из всех непараметрических методов он один из наиболее простых. Основное условие его применения — наличие двух связанных выборок, образованных по принципу «до и после» и содержащих результаты, выраженные в шкале не ниже порядковой.
Отличительная особенность теста знаков в том, что для его применения достаточно знать всего лишь то, в какую сторону (увеличения или уменьшения изменились (сдвинулись) результаты второго измерения по сравнению с первым. В том случае, если второй результат больше первого, обозначим его «+» (положительный сдвиг). Если второй результат меньше первого, обозначим его «—» (отрицательный сдвиг). Если результат не изменился, обозначим его «О» (нулевой сдвиг).
Затем подсчитывается количество положительных, отрицательных и нулевых сдвигов. В дальнейшем нулевые сдвиги игнорируются, поскольку они является признаком отсутствия изменений. Сравнение количества положительных и отрицательных сдвигов позволяет выделить типичное направление сдвига, сдвигов со знаком « + » больше, чем со знаком «—», типичное направление сдвига положительное (в выборке «после» результаты сдвинулись в сторону увеличения по сравнению с выборкой «до»). Соответственно, если сдвигов со знаком «—» больше, чем со знаком « + », типичное направление сдвига отрицательное (в выборке «после» результаты сдвинулись в сторону уменьшения по сравнению с выборкой «до»).
Сдвиги в сторону, противоположную типичному направлению сдвига, называются нетипичными. Чем меньше число нетипичных и нулевых сдвигов, тем более существенны различия «до и после» между выборками. Существуют специальные статистические таблицы для теста знаков, которые для выбранного уровня значимости α показывают, при каком числе нетипичных сдвигов различия между первой и второй выборками можно считать неслучайными.
Итак, выбираем уровень значимости α =0,05 и сформулируем нулевую и альтернативную гипотезы.
Н0: Различия между выборками носят случайный характер: ситуация с опозданиями во втором семестре не отличается от ситуации с опозданиями в первом семестре.
Альтернативная гипотеза формулируется либо в общем виде, либо в зависимости от типичного направления сдвига:
Н1 a: Различия между выборками носят неслучайный характер: ситуация с опозданиями во втором семестре отличается от ситуации с опозданиями в первом семестре (двусторонняя критическая область).
Н1 b: Различия между выборками носят неслучайный характер: опозданий во втором семестре стало больше, чем в первом (односторонняя критическая область, типичное направление сдвига положительное).
Н1с: Различия между выборками носят неслучайный характер: опозданий во втором семестре стало меньше, чем в первом (односторонняя критическая область, типичное направление сдвига отрицательное).
На основе таблицы 4.3 создадим таблицу 4.4, дополнив ее двумя новыми столбцами.
1. Для каждой пары значений «до и после» определим и запишем в таблицу направление сдвига результатов второго измерения («после») по сравнению с первым («до»):
· число пропусков во втором семестре («после») стало меньше числа пропусков в первом семестре («до»): А > В;
· число пропусков во втором семестре («после») стало больше числа пропусков в первом семестре («до»): А < В;
· число пропусков во втором семестре («после») равно числу пропусков в первом семестре («до»): А =В.
2. Определим и запишем в таблицу знак сдвига (знак определяется вычитанием из результата «после» результата «до»).
Таблица 4.4
Расчетная таблица для теста знаков
| Студент | Число пропусков в семестре А | Число пропусков в семестре В | Направление изменения | Знак изменения
| ||
| 1 | 3 | 3 | А=В | 0
| ||
| 2 | 7 | 5 | А>В | –
| ||
| 3 | 5 | 2 | А>В | –
| ||
| 4 | 8 | 6 | А>В | –
| ||
| 5 | 6 | 7 | А<В
| + | ||
| 6 | 4 | 5 | А<В
| + | ||
| 7 | 5 | 0 | А>В
| — | ||
| 8 | 7 | 4 | А>В
| — | ||
| 9 | 2 | 1 | А>В
| — | ||
| 10 | 5 | 5 | А=В
| 0 | ||
| 11 | 0 | 2 | А<В
| + | ||
| 12 | 3 | 2 | А>В
| — | ||
| 13 | 5 | 5 | А=В
| 0 | ||
| 14 | 0 | 0 | А=В
| 0 | ||
| 15 | 6 | 3 | А>В
| — | ||
| 16 | 5 | 0 | А>В
| — | ||
| 17 | 6 | 3 | А>В
| — | ||
| 18 | 0 | 1 | А<В
| + | ||
| 19 | 4 | 3 | А>В
| — | ||
| 20 | 7 | 5 | А>В
| — | ||
Подсчитаем количество отрицательных, положительных и нулевых сдвигов:
· число отрицательных сдвигов: 12;
· число положительных сдвигов: 4;
· число нулевых сдвигов: 4.
Исключаем из дальнейшего рассмотрения нулевые сдвиги (выборка уменьшится с 20 до 16 значений).
Сравниваем число отрицательных и положительных сдвигов и определяем типичное направление сдвига. Поскольку отрицательных сдвигов 12, а положительных 4, типичное направление сдвига отрицательное (количество пропусков занятий во втором семестре сдвинулось в сторону уменьшения). Очевидно, что число типичных сдвигов равно 12, число нетипичных сдвигов равно 4.
В качестве альтернативной используем гипотезу Н1с: Различия между выборками носят неслучайный характер: опозданий во втором семестре меньше, чем в первом (односторонняя критическая область, типичное направление сдвига отрицательное).
Если вернуться к нулевой гипотезе, то в ней фактически говорится о том, что с одинаковой вероятностью результаты «после» могут как возрасти, так и уменьшиться по сравнению с результатами «до». Для проверки этого утверждения необходимо сравнить эмпирическое распределение результатов «после» (сколько из них возросло, а сколько уменьшилось) с теоретическим распределением. В данном случае мы вновь вынуждены использовать биномиальный тест и формулу Бернулли (параграф 3.1).
Если считать, что результаты «после» распределены случайным образом, то существует вполне определенная вероятность того, что интересующее нас событие наступит не более 4 раз из 16 (число нетипичных сдвигов из общего числа сдвигов). Эта вероятность рассчитывается по формуле Бернулли или находится по таблице 3 (Приложение 2). Находим в таблице для N = 16 (размер выборки без нулевых сдвигов) и х=4 (число нетипичных сдвигов) значение вероятности р =0,038. Поскольку это значение меньше выбранного нами уровня значимости α =0,05, нулевая гипотеза отвергается и принимается альтернативная. Опозданий во втором семестре стало меньше, чем было в первом.
К сожалению, таблица 3 ограничена значением N=25. В случае больших выборок приходится прибегать к вычислению z (см. ниже) и использовать таблицу для z-распределения.
ВКЛЮЧАЕМ КОМПЬЮТЕР...
В программе SPSS на основе числа позитивных (np) и негативных (nn) сдвигов, а также в зависимости от величины (np + nn) используются следующие алгоритмы вычислений [SPSS Statistical Algorithms, 1986]:
1. Если (np + nn ) ≤ 25, то по формуле Бернулли рассчитывается вероятность того, что в (np + nn) случаях, в каждом из которых вероятность появления события равна р=0,5, событие наступит не более r раз, где r= min (np, nn):
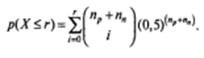
2. Если (np + nn) > 25, вычисляется значение z:
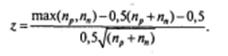
В рассмотренном выше примере np =4, nn =12, (np + nn)= 16, r= min (np, nn)=4.
Поскольку (np + nn) ≤ 25, используем формулу Бернулли:
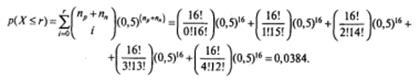
Данное значение вероятности, разумеется, совпадает с результатом, полученным в рассмотренном выше примере за счет использования таблицы 3 для биномиального распределения.
Создадим переменные «Первый семестр» (term1) и «Второй семестр» (term2), которые будут содержать сведения о числе пропусков занятий в первом и втором семестре. Дальнейшая последовательность действий, включая получаемый результат показана на рис. 4.4—4.6.

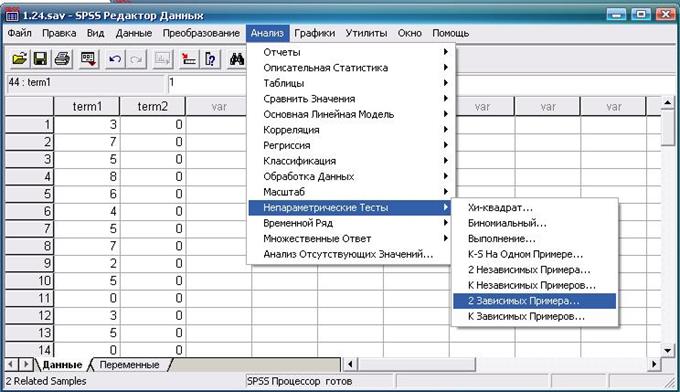
Рис. 4.4. Выбор требуемой статистической процедуры

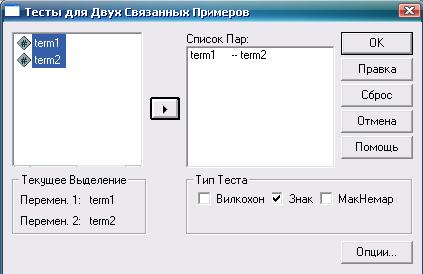
Рис. 4.5. Тест знаков: необходимые действия и настройки
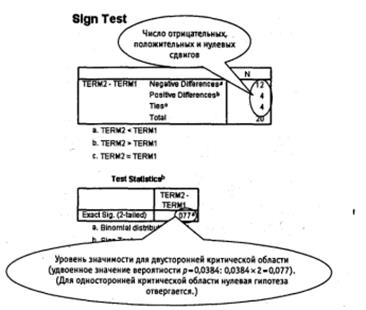
Рис. 4.6. Тест знаков: результат
Дата: 2018-12-21, просмотров: 740.