Как известно, в процессе индивидуальной или групповой терапии многие формы поведения клиентов представляют собой явные или неявные послания в адрес терапевта или других клиентов. «Расшифровка» таких посланий может дать ценную дополнительную информацию о ходе индивидуального или груп­пового терапевтического процесса. Например, в роли одного из подобных посланий могут выступать различного рода опоздания клиента, переносы или отмены им встреч с терапевтом и др.

В ходе длительной индивидуальной терапии терапевт решил сделать случаи опозданий своего клиента предметом обсуждения с ним. Предварительно, на протяжении последних 10 встреч, он фиксировал случаи своевременного (1) и несвоевременного (0) прихода клиента на сеанс терапии. В результате была получена такая последовательность:

0, 1, 0, 1, 1, 0, 1, 1, 0, 0.

Можно ли на основе полученных результатов утверждать, что опоздания клиента носят неслучайный характер?

С подобного рода задачами часто приходится иметь дело при наличии по­следовательности дихотомических значений какой-либо переменной (например, чередование мужчин и женщин в очереди, чередование черного и крас­ного цвета при игре в рулетку, чередование выигрышей и проигрышей спортивной команды и др.). Основной возникающий здесь вопрос — подчи­няется ли чередование результатов какой-либо закономерности (извечная мечта любителей рулетки — вывести «формулу успеха») или носит случайный характер.

Для ответа на данный вопрос чаще всего используется тест последователь­ностей (или серий).

Как обычно, выберем уровень значимости α = 0,05 и сформулируем нулевую и альтернативную гипотезы.

Н₀: Чередование случаев прихода клиента вовремя и с опозданием носит случайный характер.

Н₁: Чередование случаев прихода клиента вовремя и с опозданием носит неслучайный характер.

Для приведенного примера определим число случаев своевременного при­хода клиента (n₁ =5) и число случаев его прихода с опозданием (n₂ = 5). Затем определим, из скольких серий повторяющихся значений 0 или 1 состоит при­веденная последовательность, и подчеркнем их (одиночное значение нуля или единицы также образует серию):

0, 1, 0, 1, 1, 0, 1, 1, 0, 0.

Как видно, последовательность состоит из 7 серий: три серии из одного нуля, одна серия из одной единицы, две серии из двух единиц и одна серия из двух нулей.

Полученное значение (обозначим его r) сравнивается с двумя критическими значениями, которые находятся в специальной таблице, используемой для проверки последовательностей при известных значениях n₁, n₂ и α (см. табл. 6, Приложение 2).

Если полученное значение числа серий r меньше первого критического значения или равно ему, или же больше второго критического значения или равно ему, нет оснований принять нулевую гипотезу. Она отвергается на заданном уровне α. Последовательность в этом случае признается неслу­чайной¹¹.

¹¹ В любой последовательности можно найти определенное число серий. Предположения о неслучайном характере последовательности возникают тогда, когда серий или слишком мало, или слишком много. Поэтому вначале проверяется предположение о том, не слишком ли мало в

последовательности серий, чтобы она могла считаться случайной. Затем предположение о том, не слишком ли много в последовательности серий, чтобы она могла считаться случайной. Из этого, кстати, следует, что здесь используется двусторонняя критическая область.

В нашем примере r =7, n₁ = n₂ =5 и уровень значимости а=0,05. В таблице 5 находим, что первое критическое значение r _{критич1} = 2, второе критическое зна­чение r _{критич2} = 10. Поскольку ни одно из условий для отклонения нулевой ги­потезы не выполняется, она принимается. Опоздания клиента носят случайный характер.

В ряде случаев длина последовательности может быть больше возможностей статистических таблиц, рассчитанных для выборки ограниченных размеров. Например, «помешанные» на игре в рулетку могут часами наблюдать за игрой и фиксировать результаты («красное» — «черное») в надежде получить «фор­мулу успеха». Для больших выборок (больше 50 значений) используется иной подход к анализу последовательностей, основанный на свойствах нормально­го распределения и реализованный в программе SPSS.

ВКЛЮЧАЕМ КОМПЬЮТЕР...

Здесь мы вновь сталкиваемся с ситуацией, знакомой по тесту Колмогорова—Смир­нова для единственной выборки. В программе SPSS используется алгоритм вычис­лений для теста последовательностей [SPSS Statistical Algorithms, 1986; Sheskin, 2004], отличающийся от рассмотренного выше и предназначенного для случая малой выборки и вычислений вручную.

В программе SPSS рассчитывается значение z по следующей общей формуле (ис­пользуются введенные выше обозначения):

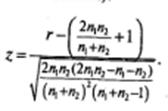
В случае маленькой выборки (менее 50 значений), в эту формулу вводится поправка:

 Подставим в формулу наши значения (r =7, n₁ = n₂ =5):

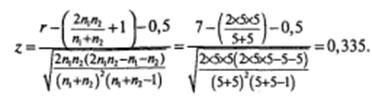
Вероятность, соответствующая найденному значению z , равна р = 0,3685. Поскольку в рассмотренном примере используется двусторонняя критическая область, иное значение вероятности удваивается: р =0,737

ПОСЛЕ СДЕЛАННЫХ ЗАМЕЧАНИЙ ПЕРЕДЕМ К ПРОГРАММЕ SPSS .

Перенесем нашу последовательность в переменную «runs».

Дальнейший порядок действий и результат показаны на рис. 3.11-3.13.

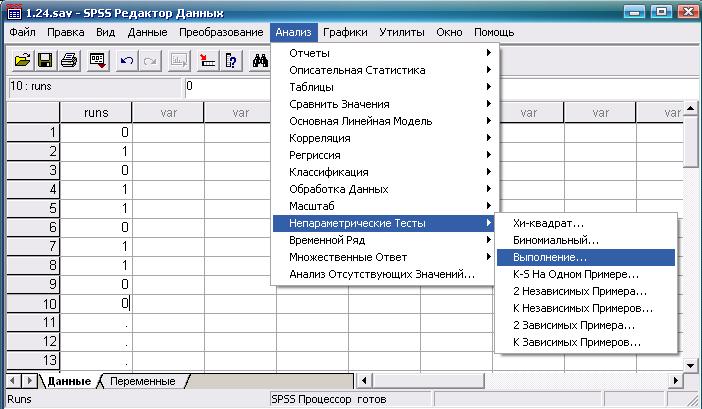
Рис. 3.11. Выбор требуемой статистической процедуры

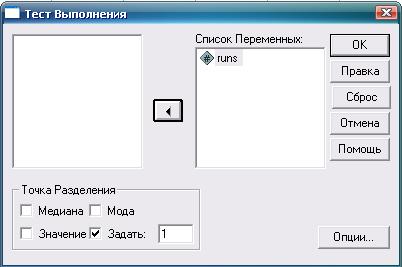
Рис. 3.12. Тест последовательностей: необходимые действия и настройки

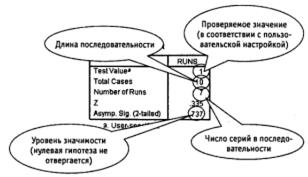
Рис. 3.13. Тест последовательностей: результат

Этим примером мы завершаем рассмотрение случая одной выборки, можно видеть из приведенных примеров, анализ одной выборки в первую очередь связан с поиском ответа на вопрос, отличается ли эмпирическое распределение результатов от теоретического, которому подчиняется популяция. В качестве теоретического распределения в приведенных примерах использовалось равномерное распределение. Разумеется, это не единственно возможный вид распределения, хотя, возможно, один из наиболее популярных для круга тех задач, которые были рассмотрены.

Следующий шаг — рассмотреть ситуацию с двумя и более выборками, которые, как известно, могут быть независимыми и зависимыми.

Глава 4 «ЧТО БЫЛО, ТО И ТЕПЕРЬ ЕСТЬ, И ЧТО БУДЕТ, ТО УЖЕ БЫЛО»¹,