| № | Номер выбранной фотографии (Х i) | 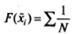
| 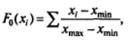
| 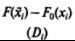
| 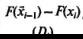
|
| 1 | 2 | 1/12 | 0 | 0,083 | 0 |
| 2 | 3 | 2/12 | 1/3 | -0,167 | -0,250 |
| 3 | 3 | 3/12 | 1/3 | -0,083 | -0,167 |
| 4 | 3 | 4/12 | 1/3 | 0 | -0,083 |
| 5 | 3 | 5/12 | 1/3 | 0,083 | 0 |
| 6 | 3 | 6/12 | 1/3 | 0,167 | 0,083 |
| 7 | 4 | 7/12 | 2/3 | -0,083 | -0,167 |
| 8 | 4 | 8/12 | 2/3 | 0 | -0,083 |
| 9 | 4 | 9/12 | 2/3 | 0,083 | 0 |
| 10 | 4 | 10/12 | 2/3 | 0,167 | 0,083 |
| 11 | 5 | 11/12 | 3/3 | -0,083 | -0,167 |
| 12 | 5 | 12/12 | 3/3 | 0 | -0,083 |
В четвертой колонке расположены значения теоретической кумулятивной функции распределения. При использовании равномерного распределения вычисление значений теоретической кумулятивной функции распределения производится по следующей формуле:
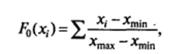
Где F 0(xi)— кумулятивная частота, соответствующая значению xi; хmin— минимальное экспериментальное значение. В нашем случае это фотография номер 2 (поскольку фотография номер 1 не получила ни одного выбора, она исключается из анализа); xmах — максимальное экспериментальное значение. В нашем примере это фотография номер 5.
В пятой колонке записана разность между значениями накопленных (кумулятивных) эмпирических и теоретических относительных частот для каждого из 12 испытуемых. В шестой колонке записана разность между предыдущим значением эмпирической кумулятивной частоты и текущим значением теоретической кумулятивной частоты. Например, для второго испытуемого значение -0,250 получается, если из предыдущего (то есть первого) значения эмпирической кумулятивной частоты, равного 1∕12 , вычесть текущее (то есть второе) значение теоретической кумулятивной частоты, равное 1∕3:
1∕12 – 1∕3 = – 0,250.
Выбираем в пятой колонке наибольшее положительное значение. Это Di =0,167.
Выбираем в шестой колонке наименьшее отрицательное значение. Это Di = -0,250.
Сравниваем их абсолютные значения и выбираем среди них наибольшее. Очевидно, что это 0,250.
После этого находим значение параметра Z, который используется в тесте Колмогорова—Смирнова для единственной выборки:
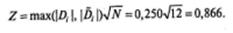
Сейчас переходим к программе SPSS.
Представим в переменной Глаза сделанные испытуемыми выводы (цифры означают, какую фотографию выбрал испытуемый). Все дальнейшие действия и получаемый результат для теста Колмогорова − Смирнова для единственной выборки показаны на рис. 3.8 −3.10.

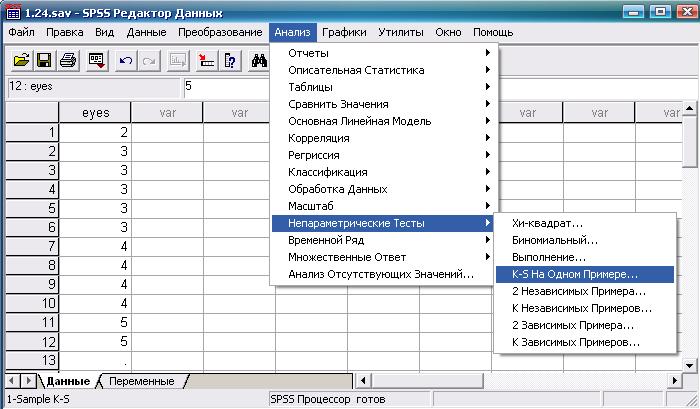
Рис. 3.8. Выбор требуемой статистической процедуры



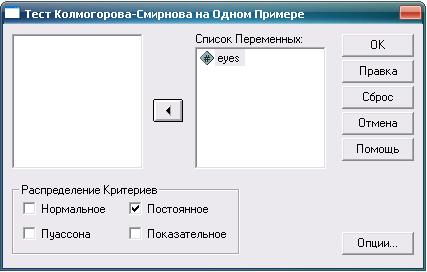
Рис. 3.9. Тест Колмогорова—Смирнова для единственной выборки: необходимые действия и настройки
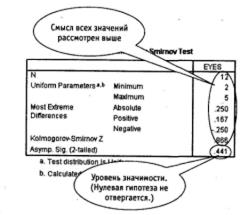
Рис. 3.10. Тест Колмогорова—Смирнова для единственной выборки: результат
ТОЧНОСТЬ - ВЕЖЛИВОСТЬ КОРОЛЕЙ»,
Дата: 2018-12-21, просмотров: 742.