| Размер глаз на фотографии в порядке возрастания | 1 | 2 | 3 | 4 | 5 | Итого |
| Теоретическая частота | 2,4 | 2,4 | 2,4 | 2,4 | 2,4 | 12 |
| Эмпирическая частота | 0 | 1 | 5 | 4 | 2 | 12 |
Для подобных задач часто применяется тест Колмогорова—Смирнова10 для единственной выборки. Он позволяет сравнивать эмпирическое распределение с теоретическим для результатов, измеренных в шкалах не ниже, чем шкала порядка.
10 Оба автора работали независимо друг от друга и решали разный круг задач. Колмогоров решал задачу сравнения эмпирического распределения с теоретическим, Смирнов — задачу сравнения двух эмпирических распределений. Поэтому в ряде случаев, когда речь идет об анализе одной выборки, говорят о тесте Колмогорова; когда анализируются две независимые выборки — ответе Смирнова [Conover, 1999].
Выберем уровень значимости α = 0,05 и сформулируем нулевую и альтернативную гипотезы.
Н0 : Эмпирическое распределение результатов выбора фотографии не отличается от равномерного.
Н1: Эмпирическое распределение результатов выбора фотографии отличается от равномерного.
Как и в случае теста Х2, вычисляется величина расхождений между теоретическим и эмпирическим распределением результатов. Но если для теста Х2 рассогласование между теоретическими и эмпирическими значениями вычислялось отдельно для каждой ячейки расчетной  таблицы, то в тесте Колмогорова — Смирнова для единственной выборки последовательно сравниваются накопленные к данному разряду таблицы эмпирические и теоретические относительные частоты. Затем определяется значение:
таблицы, то в тесте Колмогорова — Смирнова для единственной выборки последовательно сравниваются накопленные к данному разряду таблицы эмпирические и теоретические относительные частоты. Затем определяется значение:
D=max׀Fi(X) – Si(X) ׀
В этом выражении Fi(X) — накопленные к данному разряду значения относительных теоретических частот;
Si(X) — накопленные к данному разряду значения относительных эмпирических частот; D — максимальное значение разницы (по модулю) между Fi(X) и Si(X ) из всех имеющихся.
В статистической таблице для теста Колмогорова — Смирнова (случай единственной выборки) (см. табл. 4, Приложение 2) приведены критические значения D и соответствующие им значения вероятностей в зависимости от объема выборки N. Если приведенная в таблице вероятность, соответствующая найденному значению D эмпир, больше выбранного уровня значимости а, нет оснований отвергнуть нулевую гипотезу. Если приведенная в таблице вероятность меньше или равна выбранному уровню значимости α, нулевая гипотеза отклоняется и принимается альтернативная.
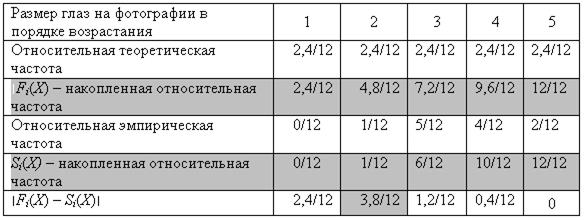
Создадим новую таблицу и проведем все необходимые вычисления. Учтем, что выражение для D не содержит данных о размере выборки. Поэтому в данном тесте используются значения относительных частот. Чтобы перейти к ним, необходимо каждое значение в таблице разделить на размер выборки (в нашем случае в выборке 12 человек). Также предусмотрим в таблице возможность для вычисления накопленных относительных частот Fi(X), Si(X ) и разности между ними. Таблица примет такой вид (табл. 3.6).
Выбираем в последней строчке максимальное значение D =3,8 : 12=0,317.
В таблице 4 (Приложение 2) в строке, соответствующей N= 12, ищем значение D, равное 0,317. Это значение находится между двумя табличными значениями D =0,296 (р =0,2) и D =0,338 (р =0,1). Можно сказать, что вероятность, соответствующая значению D эмпир =0,317, расположена между значениями р =0,2 и р =0,1, или 0,1 < р < 0,2. В любом случае это больше, чем выбранное значение уровня значимости α = 0,05. Следовательно, у нас нет оснований, чтобы отвергнуть нулевую гипотезу. Эмпирическое распределение результатов выбора фотографии не отличается от равномерного. Изменение размера глаз на фотографиях не оказало значимого влияния на результаты их выбора.
Таблица 3.6
Итоговая таблица для теста Колмогорова—Смирнова
ВКЛЮЧАЕМ КОМПЬЮТЕР...
К сожалению, компьютерный вариант теста Колмогорова—Смирнова для единственной выборки заметным образом отличается от рассмотренного выше. Данный тест был адаптирован для осуществления вычислений вручную, что не лучшим образом сказалось на его качестве. Упрощенный алгоритм вычислений сделал данный тест более удобным для использования, но менее точным, что приводит к ошибкам при проверке гипотез.
В программе SPSS этот тест реализован в своем первозданном виде. Применяемый алгоритм вычислений [SPSS Statistical Algorithms, 1986; Sheskin, 2004] отличается от того, который использовался нами в рассмотренном выше примере. Покажем, как работает неадаптированный алгоритм вычислений, а затем перейдем к программе SPSS.
Запишем результаты эксперимента в несгруппированном виде и выполним все необходимые для теста Колмогорова—Смирнова для единственной выборки вычисления (табл. 3.7).
В первой колонке расположены испытуемые, во второй — сделанные ими выборы той или иной фотографии. Испытуемые упорядочены в соответствии с номером выбранной ими фотографии.
Относительная эмпирическая частота выбора той или иной фотографии у всех испытуемых одинакова и равна 1∕12. В третьей колонке расположены значения накопленных (кумулятивных) частот, которые меняются от 1∕12 до 1 (эмпирическая кумулятивная функция распределения).
Таблица 3.7
Тест Колмогорова—Смирнова для единственной выборки:
Дата: 2018-12-21, просмотров: 829.