Вначале две ситуации.

1. Алекс и Том, два друга-студента, любители пива, предпочитают проводить свободное от учебы время за кружкой пива в одном из пабов. Но каждый раз они спорят друг с другом, какой паб предпочесть — «Пивная корова» или «Безумный Макс»? Один из них утверждает, что наиболее популярной у студентов является «Пивная корова», в то время как второй верен «Безумному Максу». С целью положить конец спорам было решено опросить других сту­дентов: какой из пабов они предпочитают. Друзьям удалось опросить 25 человек, из которых 15 предпочли «Пивную корову», а 10 — «Безумного Макса». Можно ли на основании полученных результатов утверждать, что один из пабов популярнее другого?

2. Володя и Алексей, два любителя игры в нарды, решили устроить соревнование, чтобы выяснить, кто из них лучший игрок. Они сыграли 24 партии. Володя победил в 17 партиях и объявил себя чемпионом. Алексей не согласился и заявил, что победа Володи носит случайный характер. Кто из них более прав?

Что объединяет оба примера?

Во-первых, в обоих случаях в нашем распоряжении всего одна выборка.

Во-вторых, в обоих случаях результаты представлены в дихотомической шкале наименований типа «да — нет», «согласен — не согласен» или «выиграл — проиграл».

В-третьих, в обоих случаях требуется проверить, соответствует ли распределение результатов в выборке известному (или предполагаемому) распределению результатов в популяции.

 Для решения подобных задач чаще всего используется биномиальный тест. Основу теста составляет формула Бернулли, определяющая вероятность того, что в N независимых испытаниях, в каждом из которых вероятность появления события равна р, событие наступит не более k раз:

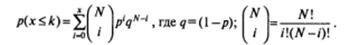
Если вернуться к первому примеру, то можно сказать, что было проделано 25 независимых испытаний (опрошено 25 студентов). Вероятность выбора в пользу первого паба примем равной вероятности выбора в пользу второго паба: р=q=0,5¹.

¹ Зачастую условие р= q =0,5 не выполняется. Например, педагоги, проводящие встречи с родителями учеников, знают, что на них чаще приходят матери учеников, чем отцы. В подобных случаях также возможно применение биномиального теста.

С помощью формулы Бернулли вычисляется вероятность того, что в пользу первого паба будет сделано не более 15 выборов из 25 (или вероятность того, что в пользу второго паба будет сделано не более 10 выборов)².

² Это аналогично ситуации, когда после 25 подбрасываний монеты «орел» выпал 15 раз и требуется определить, мог ли быть такой результат получен случайно, или мы имели дело с фаль­шивой монетой.

Как известно, если вероятность случайного наступления какого-либо со­бытия ничтожно мала, но событие тем не менее имело место, то можно говорить о нем как о неслучайном. Мы уже говорили, что в качестве границы между нашим отношением к событию как случайному или как к неслучайному вы­ступает значение уровня значимости α.

Таким образом, если событие имеет место (определенное число выборов в пользу одного из пабов), а теоретическая вероятность случайного наступления такого события ничтожна мала (меньше значения α), то это будет говорить о неслучайности полученного результата.

После этих рассуждений приступим к проверке.

Выберем уровень значимости α =0,05³ и сформулируем нулевую и альтер­нативную гипотезы.

³ В этом и последующих примерах проверка статистических гипотез осуществляется для α=0,05. Этот выбор сделан из соображений удобства и не носит принципиального характера.

Н₀: Оба паба пользуются одинаковой популярностью.

Н₁: Первый паб пользуется большей популярностью по сравнению со вторым.

В данном случае при проверке гипотезы используется односторонняя кри­тическая область. Если бы нас интересовало не то, какой из пабов более попу­лярен, а одинаковы ли они по популярности, альтернативная гипотеза выгля­дела бы следующим образом:

Н₁: Популярность пабов различна.

В этом случае необходимо было бы использовать двустороннюю критическую область.

На основании имеющихся данных можно приступать к вычислениям с ис­пользованием приведенной формулы. Подставим в нее все необходимые для вычислений значения:

k= 10⁴, р=q=0,5, N=25.

⁴ При наличии несовпадающего числа выборов в пользу каждой из альтернатив в формуле Бернулли используется меньшее из них.

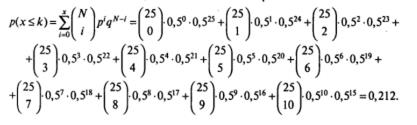
В случае использования статистической таблицы для биномиального теста необхо­димость в самостоятельных вычислени­ях отпадает. В таблице 3 (Приложение 2) для соответствующих значений N и k  ука­зывается вероятность того, что при нали­чии двух равновероятных альтернативу (р=q=0,5) сделанное число выборов в пользу одной из них может считаться случайным. Приводимые в таблице 3 значения соответствуют односторонней критической области.

Если найденное по таблице значение вероятности больше значения выбранного уровня значимости α, у нас нет оснований отвергнуть нулевую гипотезу.

Если найденное из таблицы значение вероятности меньше или равно значению уровня значимости α, нулевая гипотеза от­вергается и принимается альтернативная.

Поскольку на практике число выборов в пользу той или другой альтернати­вы редко бывает одинаковым (в нашем случае в пользу первого паба высказалось 15 студентов, а в пользу второго — 10), в таблице используется меньшее из двух чисел, обозначенное как х (то есть х=10).

Находим в таблице 3, что для N=25 и х=10 вероятность р=0,212 (что, разумеется, совпадает со значением, полученным путем самостоятельных вычислений). Поскольку р =0,212 больше значения α =0,05, у нас нет оснований отвергнуть нулевую гипотезу. Оба паба пользуются одинаковой популярностью у студентов, а различия в выборах в пользу одного и другого объясняются дей­ствием случайных факторов.

Вернемся к игрокам в нарды и разберемся в их ситуации.   

Выберем уровень значимости α =0,05 и сформулируем нулевую и альтернативную гипотезы.

Н₀: Уровень мастерства игры в нарды Володи не отличается от уровня мастерства Алексея.

Н₁:: Уровень мастерства игры в нарды Володи отличается от уровня мастерства Алексея (двусторонняя критическая область⁵).     

⁵ Альтернативная гипотеза не утверждает, что Володя играет лучше Алексея. Она лишь утвер­ждает, что они имеют различный уровень мастерства.

Нам известно, что N=24 и число побед у Алексея равно семи (выбираем меньшее из двух чисел). Вновь обратимся к таблице 3 и найдем, что для N =24 и х=7 вероятность р=0,032. Это меньше значения уровня значимости α =0,05, поэтому нулевую гипотезу можно отвергнуть и принять альтернативную.

Однако сделанный вывод неверен. Приведенные в таблице 3 значения со­ответствуют односторонней критической области. Мы же, в соответствии с альтернативной гипотезой, должны использовать двустороннюю критическую область. Вопрос о том, как от результата проверки для односторонней крити­ческой области перейти к результату для двусторонней критической области, рассматривался нами выше. Здесь действуют те же правила: для того чтобы получить результат, соответствующий двусторонней критической области, найденное значение вероятности необходимо удвоить. Получим значение р=2x0,032 = 0,064.

Новое значение вероятности (0,062) оказывается больше значения уровня значимости (0,05), поэтому нет оснований для того, чтобы отвергнуть нулевую гипотезу. Между Володей и Алексеем нет различий в уровне мастерства игры в нарды⁶.

⁶ Если бы мы сформулировали альтернативную гипотезу для односторонней критической области («Володя играет в нарды лучше, чем Алексей»), мы бы могли этот вывод принять (по­скольку 0,032 < 0,05). Однако гипотеза «Уровень мастерства игры в нарды Володи отличается от Уровня мастерства Алексея» означает двойную проверку: «Володя играет в нарды лучше, чем Алексей» и «Володя играет в нарды хуже, чем Алексей». Двойной проверки альтернативная ги­потеза не выдержала.

Если вернуться к таблице 3, то видно, что она ограничена значением N=25. В том случае, если объем выборки N> 25, для проверки гипотез обыч­но используется формула, с помощью которой вначале вычисляется значение z, а затем, с использованием таблицы z -распределения (табл. 1, Приложение 2), определяется соответствующая найденному значению z вероятность (пло­щадь под кривой нормального распределения, лежащая правее или левее z). Если полученное значение вероятности больше выбранного уровня значи­мости α, нет оснований, чтобы отвергнуть нулевую гипотезу. Если это зна­чение меньше или равно α, нулевая гипотеза отвергается и принимается альтернативная.

Значение z вычисляется по следующей формуле⁷:

⁷ Данной формулой можно пользоваться при любых значениях N, однако по сравнению с формулой Бернулли она дает менее точные результаты, особенно если N мало. Различия между результатами двух формул уменьшаются по мере роста N.

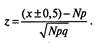
(х + 0,5) используется в том случае, когда х < N р;

(х - 0,5) используется в том случае, когда х > N р.

Подставим в эту формулу данные для первого примера (N=25, х = 10, р=q=0,5):

В таблице для z -распределения (табл. 1, Приложение 2) находим, что зна­чению z =- 0,8 соответствует вероятность р =0,2119 = 0,212, что совпадает с ранее полученным результатом. Поскольку это значение больше выбранного уровня значимости α = 0,05, у нас нет оснований, чтобы отвергнуть нулевую гипотезу.

ВКЛЮЧАЕМКОМПЬЮТЕР И ЗАПУСКАЕМ ПРОГРАММУ SPSS ⁸

⁸Общее замечание к использованию программы SPSS для приводимых в книге примеров:

1. Программой SPSS рассчитывается либо значение z, с последующим определением соответ­ствующей вероятности р, либо реальное значение вероятности ошибки первого рода (в отличие от априори выбираемого значения уровня значимости α, обычно равного 0,5; 0,01 или 0,001). В большинстве случаев получаемые в SPSS результаты, говорящие о значимости различий, соот­ветствуют двусторонней критической области.

2. Если выбранное исследователем значение α больше (или равно) тех значений, которые были рассчитаны программой SPSS, нулевая гипотеза отвергается. Если выбранное исследова­телем а меньше этих значений, нет оснований, чтобы отвергнуть нулевую гипотезу.

Для ответа на вопрос, в самом ли деле один из пивных баров более популярен, чем другой, создадим переменную «Пиво» (beer) и закодируем выбор в пользу первого паба («Безумный Макс») как 1, а выбор в пользу второго паба («Пивная корова»), как 2. Дальнейшая последовательность действий и конечный результат показаны на рисунках 3.1—3.4.

Рис. 3.1. Выбор требуемой статистической процедуры

Рис. 3.2. Биномиальный тест: необходимые действия и настройки

Рис. 3.3. Биномиальный тест: результат

Рис. 3.4. Биномиальный тест: результат (пример игроков в нарды)

ФОРД», «ФИАТ», «ТОЙОТА»,

ИЛИ ТЕСТ х²ДЛЯ ЕДИНСТВЕННОЙ ВЫБОРКИ

Покупка машины — важный этап в жизни каждой семьи. По улицам изра­ильских городов бегает несколько десятков марок автомобилей на любой вкус, но если присмотреться, то создается впечатление, что некоторые марки встре­чаются чаще других. Для проверки этого предположения Анна и Даниил, со­бравшиеся обзавестись автомобилем, решили проверить, какие машины чаще всего встречаются на улицах их города. При этом они договорились фиксиро­вать не конкретные марки машин, а то, откуда машина «родом», — Америка (США), Европа, Юго-Восточная Азия (Япония и Южная Корея) или другое (Россия, Индия, Китай и др.). Случайным образом было проверено 80 машин, которые распределились в зависимости от места производства следующим образом (табл .3.1).

Таблица 3.1