| Место выпуска | Америка | Европа | Азия | Другое | Итого |
| Количество | 17 | 23 | 32 | 8 | 80 |
Можно ли на основании полученных данных сказать, что все машины пользуются одинаковой популярностью?
Основное отличие данной задачи от предыдущей в том, что сейчас результаты распределены по более чем двум категориям (в данном случае по четырем категориям). Остальные условия те же самые: одна выборка и необходимость проверить, соответствует ли распределение результатов в выборке известному (или предполагаемому) распределению результатов в популяции.
Для решения подобных задач применяется один из наиболее популярных непараметрических тестов — тест х2. На страницах этой книги он будет встречаться не один раз.
 Существует два основных типа задач, решаемых с помощью этого теста.
Существует два основных типа задач, решаемых с помощью этого теста.
Во-первых, сравнение эмпирического распределения качественных признаков с теоретическим. Во-вторых, сравнение между собой двух и более эмпирических распределений качественных признаков. При наличии достаточно большой выборки тестом х2 можно пользоваться вместо биномиального теста.
Что касается вида теоретического распределения, то в нашем случае используется равномерное распределение. Смысл его в том, что все результаты считаются равновероятными. При наличии четырех стран-производителей автомобилей вероятность встретить машину, произведенную в какой-либо из них, должна быть одна и та же и равна 1/4 = 0,25. Иными словами, если бы эмпирическое распределение результатов полностью совпало с теоретическим, то в каждую ячейку таблицы попало бы одинаковое число машин, равное 80:4 = 20.
С учетом данного обстоятельства запишем окончательный вариант расчетной таблицы для нашего примера (табл. 3.2).
Таблица 3.2
Теоретическое и эмпирическое распределение автомобилей
По странам-производителям
| Место выпуска | Америка | Европа | Азия | Другое | Итого |
| Теоретическое количество | 20 | 20 | 20 | 20 | 80 |
| Эмпирическое количество | 17 | 23 | 32 | 8 | 80 |
Дальнейший алгоритм действий прост.
Формулируем нулевую и альтернативную гипотезы и задаем уровень значимости α=0,05.
Н0: Все страны-производители машин представлены одинаковым образом (вероятность встретить на дороге машину, произведенную, например, в США, равна вероятности встретить машину, произведенную в Европе или в Юго-Восточной Азии, и т. д.).
Н1: Различные страны-производители машин представлены неодинаковым образом (вероятность встретить машину, произведенную в США, не равна вероятности встретить машину, произведенную в Европе, в Юго-Восточной Азии и т. д.).
Затем вычисляется сумма отклонений между наблюдаемыми и теоретическими значениями по формуле:
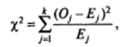
где Оj — наблюдаемые (observed), или эмпирические, значения (частоты) для каждой из категорий таблицы 3.2; Еj — ожидаемые (expected), или теоретические, значения (частоты) для каждой из категорий таблицы 3.2; k — количество категорий в таблице 3.2.
С учетом введенных обозначений перейдем от таблицы 3.2 к таблице 3.3.
Подставим соответствующие значения Оj и Еj в расчетную формулу:
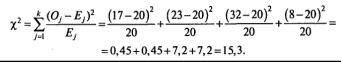
Таблица 3.3
Дата: 2018-12-21, просмотров: 768.