Наделение объектов именами позволяет приступить к выявлению сходств и различий между ними. Например, можно обнаружить, что одни студенты более успешны, чем другие, автомобили одних марок быстрее автомобилей других марок, одни блюда вкуснее других и т. д.
В том случае, когда между объектами возможно установление отношений типа «быстрее», «успешнее», «вкуснее», «ярче», «громче», «тверже», «популярнее» и др., появляется возможность расположить объекты в порядке возрастания или убывания определенного признака. После этого остается наделить упорядоченную последовательность числами таким образом, чтобы, например, большее число соответствовало большей степени выраженности признака. В результате получим шкалу порядка, в которой отношения между числами будут соответствовать отношениям между объектами. Такие шкалы широко ^ используются в повседневной жизни.
Одна из наиболее распространенных шкал порядка — шкала школьной или университетской успеваемости. Чем более успешен студент, тем большее число в этой шкале ему соответствует. Существуют и другие, столь же широко применяемые шкалы порядка, например шкала твердости минералов Мооса, шкала Бофорта для силы ветра, сейсмические шкалы для оценки силы землетрясений и др.
В то же время расположение объектов в порядке возрастания определенного свойства (например, минералов по твердости) еще не дает ответа на вопрос: на сколько больше? Шкала порядка не позволяет определить «расстояние» между объектами. Об этом особенно необходимо помнить в тех случаях, когда из соображений удобства шкальные значения отделяют друг от друга равные интервалы. Например, четыре студента получили на экзамене оценки 75, 85, 90 и 100 баллов. Оценка второго студента отличается от оценки первого также, как оценка четвертого студента отличается от оценки третьего, — на 10 баллов.
 Но из этого не следует, что знания второго студента больше знаний первого на столько же, на сколько знания четвертого больше знаний третьего.
Но из этого не следует, что знания второго студента больше знаний первого на столько же, на сколько знания четвертого больше знаний третьего.
Шкала Мооса содержит значения от 1 до 10, но из этого не следует, что гипс (вторая позиция в шкале) тверже талька (первая позиция) на столько, на сколько алмаз (десятая позиция) тверже корунда (девятая позиция).
Таким образом, выбор чисел, используемых в шкале порядка, в известных пределах произволен. Числа могут быть любыми, но они должны подчиняться основному требованию: объекту с большей выраженностью определенного признака должно быть приписано большее число. Так, наши суждения о студентах по результатам экзамена не изменились бы при переходе, например, к шкале оценок от 0 до 50. В любом случае более успевающий студент получил бы более высокую оценку.
Особенности шкалы порядка позволяют определить для нее группу допустимых математико-статистических преобразований. Результаты, представленные в шкале порядка, нельзя использовать для пропорций (знания, оцененные на 100, не являются вдвое большими знаний, оцененных на 50). Эти результаты нельзя складывать (знания получившего на экзамене 100 баллов не равны сумме знаний получивших 40 и 60 баллов). Если говорить о мерах центральной тенденции, то из них можно применять только моду и медиану. Вычисление среднего (например, средней успеваемости) является недопустимой операцией для шкалы порядка (к сожалению, это требование повсеместно нарушается).
Шкалы порядка широко используются в психологии, социальной работе, педагогике и др. Многие непараметрические методы статистики были специально разработаны для шкал порядка. С этими шкалами связана одна из наиболее популярных в непараметрической статистике процедур — процедура ранжирования.
Если какие-либо результаты расположены в порядке возрастания или убывания, то можно определить, какое место занимает каждый из них. Ранжирование — это процедура определения места, которое должен занять данный результат в упорядоченной последовательности всех результатов.
Часто ранжирование идет по направлению убывания каких-либо значений (например, оценок на экзамене). Тогда первый, наивысший ранг получает обладатель наибольшего значения (например, обладатель наивысшей оценки).
Допустим, 11 студентов получили на экзамене следующие оценки3:
3 В Израиле используется 100-балльная шкала академической успеваемости.
| Оценка | 80 | 88 | 94 | 96 | 83 | 95 | 90 | 85 | 100 | 93 | 86 |
Необходимо проранжировать полученные оценки и определить, какое место (ранг) каждая из них занимает. Вначале упорядочим результаты в порядке убывания:
| Оценка | 100 | 96 | 95 | 94 | 93 | 90 | 88 | 86 | 85 | 83 | 80 |
Сейчас определим, какое место (ранг) занимает каждая из них:
| Оценка | 100 | 96 | 95 | 94 | 93 | 90 | 88 | 86 | 85 | 83 | 80 |
| Ранг | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
Обратите внимание, что «расстояние» между рангами не соответствует «расстоянию» между оценками: ранги отстоят друг от друга с постоянным интервалом 1, а интервал между оценками колеблется от 1 до 4. В этом проявляется та особенность шкалы порядка, о которой мы говорили: в данной шкале можно определить порядок следования результатов (этот порядок задается рангами), но нельзя определить, насколько один результат отличается от другого.
Трудности, возникающие в процессе ранжирования, связаны с ситуацией, когда среди значений встречаются повторяющиеся. Это приводит к возникновению так называемых связанных рангов.
Например, 11 студентов получили на экзамене следующие оценки:
| Оценка | 88 | 94 | 96 | 90 | 92 | 88 | 100 | 88 | 86 | 92 | 98 |
Как и прежде, необходимо проранжировать полученные оценки и определить ранг каждой из них. Упорядочим результаты в порядке убывания:

Как видно из результатов, оценка 92 повторяется дважды, а оценка 88 — трижды. При ранжировании ранги совпадающих значений не должны отличаться друг от друга4.
4 Здесь как в спорте. Если два бегуна показали одинаковый результат, наилучший среди результатов остальных бегунов, то они делят между собой первое и второе место. Фактически ранг каждого из них равен 1,5.
В том случае, если среди ранжируемых результатов встречаются группы одинаковых значений, ранг внутри каждой из таких групп определяется как среднее арифметическое тех рангов, которые имели бы результаты, будь они отличными друг от друга.
Предположим, что совпадающие результаты немного отличаются друг от друга:
| Оценка | 100 | 98 | 96 | 94 | 92,1 | 92,2 | 90 | 88,1 | 88,2 | 88,3 | 86 |
В этом случае проблема ранжирования решается просто:

Найдем среднее арифметическое рангов для искусственно измененных значений:
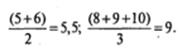
Вернемся к исходным данным и припишем повторяющимся значениям
одинаковые (связанные) ранги:

Рассмотрим еще пример.
В таблице 1.5 были приведены значения IQ родителей и их детей.
Проранжируем эти значения и создадим новую таблицу, где вместо значений 10 будут стоять соответствующие ранги.
Поскольку значения IQ родителей уже упорядочены по возрастанию, можно сразу приступить к процедуре ранжирования (так как значения IQ упорядочены по возрастанию, первый ранг будет приписан наименьшему значению IQ). Среди значений IQ много повторяющихся, поэтому при ранжировании получим много связанных рангов (табл. 2.3).
Таблица 2.3
Дата: 2018-12-21, просмотров: 713.