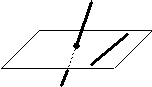
Расстояние между скрещивающимися прямыми

Общий перпендикуляр к двум скрещивающимся прямым

Угол между скрещивающимися прямыми
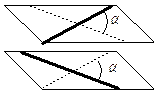
|
Углы в пространстве | |
|
Угол между прямой и плоскостью | |

| Так называется угол между прямой и ее проекцией на плоскость. |
|
Двугранный угол | |
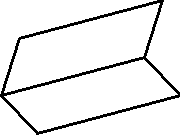
| Так называется фигура, образованная двумя полуплоскостями с общей ограничивающей их прямой (эта прямая называется ребром двугранного угла). |
|
Линейный угол двугранного угла | |

| Так называется угол между двумя лучами, образующимися при пересечении двугранного угла плоскостью, перпендикулярной ребру двугранного угла. Мерой j двугранного угла является мера соответствующего ему линейного угла: 00 < j < 1800. |
|
Угол между плоскостями | |

| Две пересекающиеся плоскости определяют четыре двугранных угла. Сумма двух таких углов, имеющих общую грань, равна 1800. Углом между плоскостями называют меньший из этих углов:
00 < j 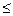 900. (Если j =900, плоскости перпендикулярны.) 900. (Если j =900, плоскости перпендикулярны.)
|
|
УПРАЖНЕНИЯ | ||
| 1. ABCDA 1 B 1 C 1 D 1 – куб. | ||
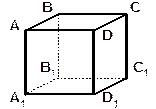
| 1. Выпишите: а) ребра, перпендикулярные плоскостям АВС, DCC1, ABB1; б) плоскости, перпендикулярные ребру ВС, ВВ1, А1D1. 2. Используя символы ^ и ||, запишите: а) как расположены прямые DD1 и CC1, АА1 и А1В1, DC и ВС; | |
| б) как расположены прямая и плоскость СС1 и DCB, АА1 и DCD1, D1C1 и DCB, В1С1 и DCB. 2. Как расположены прямая a и b, если: а) прямые a,b и с лежат в плоскости a, прямая m ^ a, m ^ b, но m не перпендикулярна с; б) прямая a ^ a, b || a, a и b лежат в плоскости b; в) прямая a || a, b ^ a, но прямая b не пересекает прямую a. 3. Как расположены прямые b и с, если: а) прямые a, b и c лежат в плоскости a, m ^ c, m ^ b, но m не перпендикулярна a; б) прямые b и с лежат в плоскости a, a ^ b, a ^ с, но прямая а не перпендикулярна a. 4. Прямая а ^ a, прямая b || a, причем a и b лежат в плоскости b. Как расположены плоскости a и b. 5. Плоскости a и b перпендикулярны, a 6. SABCD – правильная пирамида (ABCD – квадрат, O – центр). | ||
|
| Выпишите: а) расстояние от точки S до плоскости АВСD; б) проекции всех ребер на плоскость основания АВСD; в) расстояние от точки S до сторон основания ABCD и их проекции. | |
| 7. SABC – правильная пирамида ( Укажите, как обозначено: а) расстояние от точки S до плоскости АВС; б) проекции всех рёбер на плоскость основания ABCD; в) расстояние от точки S до сторон основания и их проекции. |
| ||||
| 8. Из точки А, данной на расстоянии 12 см, проведена наклонная. Найдите: а) длину наклонной, если её проекция равна 5 см; б) определите проекцию наклонной, если наклонная равна 20 см. |
| ||||
| 9. Под каким углом к плоскости надо провести наклонную, чтобы: а) перпендикуляр был в два раза меньше наклонной; б) проекция и длина перпендикуляра были равны. 10. Из одной точки к плоскости проведены две наклонные. Одна имеет проекцию 2 м, а другая 3 м. Какая из наклонных образует с плоскостью меньший угол. | |||||
| 11. Через вершину острого угла прямоугольного треугольника АВС с прямым углом С проведена прямая АD. АD перпендикулярна плоскости треугольника. Чему равно расстояние от точки D до вершины С, если АС = 6см., АD = 8 см.? | 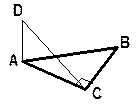
| ||||
| 12. Отрезок АВ длиной 10 дм своими концами упирается в две параллельные плоскости a и b, расстояние между которыми равно 8 дм. Найдите проекции отрезка на эти плоскости. | 
| ||||
|
13.
|
Из точки М, отстоящей от плоскости на расстоянии 6 см, проведены к этой плоскости наклонные МА и МВ, образующие с ней углы 450 и 300, а между собой прямой угол. Найдите расстояние между основаниями наклонных. | ||||
|
14.
|
На изображении прямоугольного параллелепипеда ABCDA1B1C1D1 укажите общий перпендикуляр прямых: AD и СС1, A1B1 и CB, АВ и DD1, СВ и АА1. Укажите длину каждого найденного перпендикуляра, если длины сторон основания А1В1=10см, D1A1=8см, а высота параллелепипеда АА1=6 см. | ||||
|
15.
|
Ребро куба ABCDA1B1C1D1 равно а. Найдите расстояние d между прямыми: 1) АВ и СС1; 2) СС1 и В1D1; 3) АС и В1D1; 4) СС1 и ВD1. | ||||
| 16. На изображении куба ABCDA1B1C1D1 постройте общий перпендикуляр прямых: СС1 и D1B1, DB и А1С1. Найдите расстояние между этими прямыми, если ребро куба равно b. 17. Докажите, что все прямые, проходящие через данную точку М прямой а и перпендикулярные к этой прямой, лежат в плоскости, проходящей через точку М и перпендикулярной к прямой а. 18. Луч ВА не лежит в плоскости неразвёрнутого угла СВD. Докажите, что если ÐАВС = ÐАВD, причём ÐАВС<900, то проекцией луча ВА на плоскость СВD является биссектриса угла СВD. | |||||
| 19. Даны два двугранных угла, у которых одна грань общая, а две другие грани являются различными полуплоскостями одной плоскости. Докажите, что сумма этих двугранных углов равна 1800. 20. Плоскости плоскости 21. Плоскости
| |||||
|
ПРОЧИТАЙТЕ УСЛОВИЕ ЗАДАЧ И РАЗБЕРИТЕ ИХ РЕШЕНИЕ | |||||
Дата: 2018-12-21, просмотров: 1265. | |||||
 b = с. Прямая а ^ с, прямая b ^ c. Как расположены прямые a и b.
b = с. Прямая а ^ с, прямая b ^ c. Как расположены прямые a и b.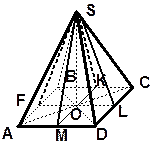
 АВС- правильный, OS – высота, O – центр вписанной окружности).
АВС- правильный, OS – высота, O – центр вписанной окружности).
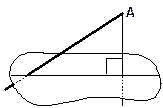
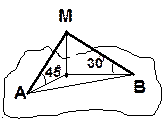
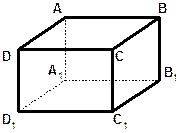
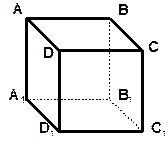
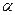 и
и 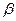 взаимно перпендикулярны. Через некоторую точку
взаимно перпендикулярны. Через некоторую точку