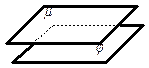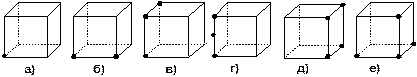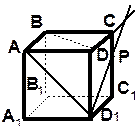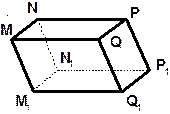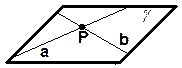
Взаимное расположение прямых в пространстве

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Две прямые, которые не лежат в одной плоскости и не имеют общих точек, называются скрещивающимися.

Две прямые, имеющие ровно одну общую точку, называются пересекающимися.

Две прямые называются параллельными, если они лежат в одной плоскости и не имеют общих точек (не пересекаются).

Взаимное расположение

Прямой и плоскости

Двух плоскостей

a = А а ^ a

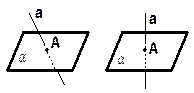Прямая и плоскость пересекаются, если у них только одна общая точка.

a 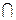b = a a ^ b

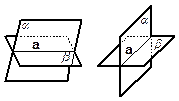
Две плоскости пересекаются, если множество их общих точек есть прямая.

Взаимное расположение (продолжение)
Прямой и плоскости	Двух плоскостей
а \|\| g 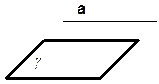Прямая и плоскость параллельны, если они не имеют общих точек.	j \|\| m Две плоскости параллельны, если не имеют общих точек.
ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ Так называются прямые, которые лежат в одной плоскости и не пересекают её.
Признак параллельности прямых
		Две прямые, параллельные третьей, параллельны между собой: (а ¹ b , а \|\| с, b \|\| с) Þ а \|\| b .
ПАРАЛЛЕЛЬНЫЕ ПРЯМАЯ И ПЛОСКОСТЬ Прямая и плоскость называются параллельными, если они не пересекаются.
Признак параллельности прямой и плоскости
		Если прямая, не принадлежащая данной плоскости, параллельна одной из прямых этой плоскости, то она параллельна этой плоскости: (b \|\| a, b Ï a , a Î a ) Þ b \|\| a .

Свойство прямой, параллельной данной плоскости
		Любая плоскость, проходящая через прямую параллельную данной плоскости, либо параллельна этой плоскости, либо пересекает её по прямой, параллельной данной плоскости: (b Î b , b \|\| a) Þ b \|\| a или a \|\| b.
ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ Так называются плоскости, которые не пересекаются (не имеют общих точек).
Признаки параллельности плоскостей
	Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны: (a₁ \|\| a ₂, b₁ \|\| b₂) Þ a \|\| b .
	Если каждая из двух данных плоскостей параллельна третьей плоскости, то данные две плоскости параллельны между собой: ( a ¹ b , a \|\| g , b \|\| g ) Þ a \|\| b .

Свойства параллельных плоскостей
	Если две параллельные плоскости пересекаются третьей плоскостью, то линии пересечения плоскостей параллельны: a \|\| b Þ a \|\| b .
	Отрезки параллельных прямых, заключенные между двумя параллельными плоскостями, равны: ( a \|\| b , a \|\| b) Þ AB = CD.

УПРАЖНЕНИЯ
1. По рисунку ответьте на вопросы.
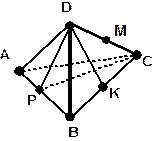
	1. Каким плоскостям принадлежит точка: А, М, К, D, Р? 2. Вне каких плоскостей лежит точка: М, К, А, Р, D? 3. На каких плоскостях лежат прямые: DB, DK, АВ, РС, АС? 4. В какой точке пересекаются прямая и плоскость: а) AD и АВС;
б) BD и ADC; в) DK и АВС; г) РС и ADB; д) AD и PDC? 5. По какой прямой пересекаются плоскости: а) АВD и BDC; б) АВС и ADC; в) АВС и АВD; г) ABD и АDC; д) PDC и АВС? 6. Какие прямые лежат на плоскостях: а) АВС; б) ABD; в) BDC?

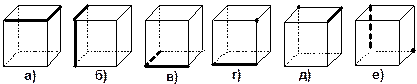
2. Сколько плоскостей можно провести через выделенные элементы куба? Заштрихуйте соответствующие плоскости грани куба. 3. Сколько граней проходит через: а) одну, б) две, в) три, г) четыре точки, выделенные на рисунке куба? Сколько плоскостей можно провести через те же точки? Определится ли при этом положение плоскости однозначно? 4. ABCDA₁B₁C₁D₁ – куб.
		1. Перечислите все ребра: а) пересекающие ребро DD₁; б) параллельные ребру АD; в) скрещивающиеся с ребром DC. 2. Запишите как располагаются прямые: а) АD₁ и D₁C₁; б) AD₁ и ВС₁; в) AD₁ и СС₁; г) AD₁ и BC₁; д) AD₁ и В₁С₁.
3. Найдите точки пересечения прямых: а) DC и СС₁; б) DC и D₁P; в) ВР и В₁С₁; г) AD₁ и D₁P. 4. Найдите: а) ребра, параллельные с DD₁ и пересекающиеся с С₁В₁; б) ребра, скрещивающиеся с АВ и пересекающие D₁C₁; в) ребро, параллельное DC и скрещивающееся с D₁A₁.
5. MNPQM ₁ N ₁ P ₁ Q ₁ – наклонный параллелепипед
		По рисунку перечислите: 1. все видимые грани; 2. все невидимые грани; 3. попарно параллельные прямые в плоскости видимого основания; 4. попарно параллельные прямые в плоскости видимой боковой грани;
5. попарно параллельные прямые в плоскости невидимого основания; 6. попарно параллельные прямые в плоскости невидимой боковой грани; 7. пару пересекающихся прямых в плоскости видимого основания; 8. пару пересекающихся прямых в плоскости невидимого основания; 9. пару пересекающихся прямых в плоскости видимой боковой грани; 10. пару пересекающихся прямых в плоскости невидимой боковой грани; 11. пару скрещивающихся прямых, одна из которых лежит в плоскости видимого основания; 12. пару скрещивающихся прямых, одна из которых лежит в плоскости невидимого основания;
6. ABCDA ₁ B ₁ C ₁ D ₁ – прямой параллелепипед.
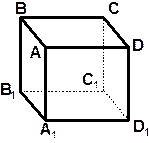
	1. Выпишите все попарно параллельные грани. 2. По каким прямым пересекаются: а) плоскости АВС и А₁В₁С₁ с плоскостями А₁АD и В₁ВС? б) плоскости АВВ₁ иDCC₁ с плоскостями А₁АD иВ₁ВС? Как расположены между собой эти прямые пересечения плоскостей? Ответ обоснуйте.

7. ABCDA ₁ B ₁ C ₁ D ₁ – куб.

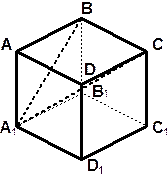
1. По каким прямым пересекаются плоскости:

а) А₁ВС и АВС; б) А₁ВС и А₁В₁С₁;

в) А₁ВС и АВВ₁; г) А₁ВС тDCC₁?

Перерисуйте чертеж в тетрадь и проведите недостающие прямые.

2. Как попарно расположены найденные прямые пересечения плоскостей? Ответ обоснуйте.

Дата: 2018-12-21, просмотров: 1041.

⇐ Предыдущая 1 2 3 456 7 8 9 10 Следующая ⇒