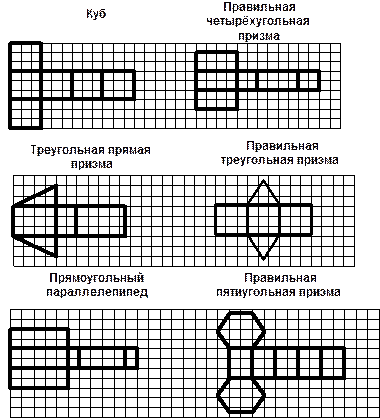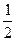 Pосн. × L,
где L – апофема.
Pосн. × L,
где L – апофема.
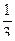 H × Sосн.
H × Sосн.
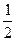 (Р + р) × L,
где Р и р – периметр верхнего и нижнего основания.
(Р + р) × L,
где Р и р – периметр верхнего и нижнего основания.
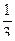 H × (S+s +
H × (S+s + 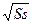 )
)
| 1 | 2 | 3 |
| Тела вращения 1. Цилиндр 2. Конус а) усечённый. 3. Шар 4. Сфера | Sосн. = p R2 Sбок. = 2 p RH Sц = 2 p R ×( R + H) Sк = Sосн. + Sбок. Sбок. = p RL Sк = p R( R + L) Sус.к = p( R + r) L + p( R2+ r2) Sбок. = p (R + r)L -------------- Sсф . = 4 p R2 | Vц . = p R2H
Vк . = 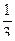 p R2H
Vус .к . = p R2H
Vус .к . = 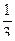 p H(R2+Rr+r)
Vш. = p H(R2+Rr+r)
Vш. = 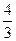 p R3
------------- p R3
-------------
|
| 5.1 УПРАЖНЕНИЯ |
| 1. Что больше: объём куба с ребром 5см или объём шара с тем же радиусом? 2. Если радиус шара увеличить в 3 раза, то во сколько раз увеличится его объём? 3. Высота конуса равна его диаметру. Найти отношение площади его основания к площади боковой поверхности. 4. Площадь большого круга равна 1м2. Найдите поверхность шара. 5. Найдите объём тела, полученного при вращении квадрата со стороной а вокруг стороны. 6. Радиусы оснований усечённого конуса 3м и 6м, высота равна 4м. Найдите образующую конуса. |
| 7. Во сколько раз увеличится боковая поверхность цилиндра, если его высота увеличится в 5раз, а радиус останется прежним? 8. Как изменится поверхность шара, если радиус увеличится в 4 раза? 9. Объём куба равен 125м3. Чему будет равна площадь его поверхности? 10. Ребро наклонной призмы равно 13см, а перпендикулярным сечением является ромб со стороной 5см. Вычислите площадь боковой поверхности призмы. 11. В прямой треугольной призме все рёбра равны. Площадь боковой поверхности равна 48см2. Найдите высоту призмы. 12. Площадь сечения правильной треугольной призмы, проходящего через средние линии оснований, равна Q. Определите площадь боковой поверхности призмы. 13. Измерения прямоугольного параллелепипеда 8, 9, 12. Найдите его объём. 14. Три латунных куба с рёбрами 3см, 4см и 5см переплавлены в один куб. Какое объём этого куба? 15. Если каждое ребро куба увеличить на 2см, то его объём увеличится на 98см3. Чему равно ребро куба? 16. Если каждое ребро куба увеличить на 1м, то его объём увеличится в 125 раз. Найдите ребро. 17. Ребро правильного тетраэдра равно 4см. Найдите его объём. 18. Ребро октаэдра равно 6м. Найдите его объём. 19.Диаметр одного шара равен радиусу другого. Чему равно отношение: а) радиусов этих шаров; б) объёмов этих шаров? |
| 5.2 ЗАДАЧИ |
1. Призма
1.1. В основании прямоугольного параллелепипеда лежит ромб, диагонали которого равны 12см и 16см. Высота параллелепипеда 8см. Найдите площадь его полной поверхности.
1.2. Диагональ правильной четырёхугольной призмы наклонена к плоскости основания под углом 600. Найдите объём призмы, если диагональ основания равна 4 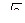 см. см.
|
1.3. В правильной четырёхугольной призме диагональ боковой грани 3,5м., а диагональ боковой грани 2,5 м. Найдите объём призмы.
1.4. Через два противолежащих ребра куба проведено сечение, площадь которого равна 64 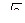 см2. Найдите площадь полной поверхности куба.
1.5. В прямом параллелепипеде стороны основания равны 6м и 8м и образуют угол в 300; боковое ребро равно 5м. Определите полную поверхность этого параллелепипеда.
1.6. В прямой треугольной призме все рёбра равны. Боковая поверхность равна 12м2. Найдите объём призмы.
1.7. Расстояние между параллельными прямыми, содержащими боковые рёбра наклонной треугольной призмы, равны 2см, 3см и 4см, а боковые рёбра 5см. Найдите боковую поверхность призмы.
1.8. В прямом параллелепипеде стороны основания 3см и 8см, угол между ними 600. Боковая поверхность равна 220см2. Найдите полную поверхность.
1.9. Основание прямой призмы – прямоугольный треугольник с катетом 6см и острым углом 450. Объём призмы равен 108см3. Найдите площадь полной поверхности призмы.
1.10.Основание прямой призмы – равнобочная трапеция, одно из оснований которой в два раза больше другого. Непараллельные боковые грани призмы – квадраты. Высота призмы равна 6см. Площадь боковой поверхности призмы равна 144см2. Вычислите объём призмы. см2. Найдите площадь полной поверхности куба.
1.5. В прямом параллелепипеде стороны основания равны 6м и 8м и образуют угол в 300; боковое ребро равно 5м. Определите полную поверхность этого параллелепипеда.
1.6. В прямой треугольной призме все рёбра равны. Боковая поверхность равна 12м2. Найдите объём призмы.
1.7. Расстояние между параллельными прямыми, содержащими боковые рёбра наклонной треугольной призмы, равны 2см, 3см и 4см, а боковые рёбра 5см. Найдите боковую поверхность призмы.
1.8. В прямом параллелепипеде стороны основания 3см и 8см, угол между ними 600. Боковая поверхность равна 220см2. Найдите полную поверхность.
1.9. Основание прямой призмы – прямоугольный треугольник с катетом 6см и острым углом 450. Объём призмы равен 108см3. Найдите площадь полной поверхности призмы.
1.10.Основание прямой призмы – равнобочная трапеция, одно из оснований которой в два раза больше другого. Непараллельные боковые грани призмы – квадраты. Высота призмы равна 6см. Площадь боковой поверхности призмы равна 144см2. Вычислите объём призмы.
|
| 2. Пирамида |
2.1. Апофема правильной треугольной пирамиды равна 6дм., а сторона основания 6 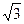 дм. Найдите площадь полной поверхности пирамиды.
2.2. В правильной четырёхугольной пирамиде сторона основания равна 10см, а высота – 12см. Найдите площадь полной поверхности пирамиды.
2.3. В правильной четырёхугольной пирамиде высота равна 7м, а боковое ребро наклонено к плоскости основания под углом 450. Найдите объём пирамиды. дм. Найдите площадь полной поверхности пирамиды.
2.2. В правильной четырёхугольной пирамиде сторона основания равна 10см, а высота – 12см. Найдите площадь полной поверхности пирамиды.
2.3. В правильной четырёхугольной пирамиде высота равна 7м, а боковое ребро наклонено к плоскости основания под углом 450. Найдите объём пирамиды.
|
2.4. Основание пирамиды – прямоугольник со сторонами 6см и 8см. Все боковые рёбра равны 13см. Найдите объём пирамиды.
2.5. Основание пирамиды – ромб с диагоналями 6м 8м. Высота пирамиды опущена в точку пересечения его диагоналей. Меньшие боковые рёбра пирамиды равны 5м. Найдите объём пирамиды.
2.6. Каждая боковая грань правильной треугольной пирамиды наклонена к плоскости основания под углом 300. Найдите площадь полной поверхности пирамиды, если её высота равна 10мм.
2.7. Дана четырёхугольная пирамида в основании которой лежит прямоугольник со сторонами 6дм. и 2 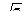 дм. Каждое боковое ребро наклонено к плоскости основания под углом 600. Найдите объём пирамиды.
2.8. В правильной треугольной пирамиде боковое ребро равно 4см, а сторона основания – 6см. Найдите площадь полной поверхности пирамиды.
2.9. Основанием пирамиды DABC является треугольник, в котором АВ = 20см, АС = 29см, ВС = 21см. Грани DAB и DAC перпендикулярны к плоскости основания, а грань DBC составляет с ней угол в 600. Найдите объём пирамиды.
2.10. В основании пирамиды лежит прямоугольный треугольник, гипотенуза которого равна 13м., а один из катетов-12м.Через середину высоты пирамиды, параллельно её основанию проведёно сечение. Найдите объём полученной усечённой пирамиды.
2.11. Стороны оснований правильной усечённой треугольной пирамиды 4дм. и 1дм. Боковое ребро 2дм. Найдите площадь полной поверхности усечённой пирамиды. дм. Каждое боковое ребро наклонено к плоскости основания под углом 600. Найдите объём пирамиды.
2.8. В правильной треугольной пирамиде боковое ребро равно 4см, а сторона основания – 6см. Найдите площадь полной поверхности пирамиды.
2.9. Основанием пирамиды DABC является треугольник, в котором АВ = 20см, АС = 29см, ВС = 21см. Грани DAB и DAC перпендикулярны к плоскости основания, а грань DBC составляет с ней угол в 600. Найдите объём пирамиды.
2.10. В основании пирамиды лежит прямоугольный треугольник, гипотенуза которого равна 13м., а один из катетов-12м.Через середину высоты пирамиды, параллельно её основанию проведёно сечение. Найдите объём полученной усечённой пирамиды.
2.11. Стороны оснований правильной усечённой треугольной пирамиды 4дм. и 1дм. Боковое ребро 2дм. Найдите площадь полной поверхности усечённой пирамиды.
|
| 3. Цилиндр |
3.1. Осевым сечением цилиндра является квадрат, диагональ которого равна 3 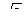 см. Найдите площадь поверхности цилиндра.
3.2. Прямоугольник, стороны которого равны 6см и 4см, вращается около меньшей стороны. Найдите площадь поверхности тела вращения.
3.3. Найдите объём тела, полученного вращением прямоугольника со сторонами 6м и 10м вокруг прямой, проходящей через середины его больших сторон. см. Найдите площадь поверхности цилиндра.
3.2. Прямоугольник, стороны которого равны 6см и 4см, вращается около меньшей стороны. Найдите площадь поверхности тела вращения.
3.3. Найдите объём тела, полученного вращением прямоугольника со сторонами 6м и 10м вокруг прямой, проходящей через середины его больших сторон.
|
| 3.4. Площадь осевого сечения цилиндра равна 20см2. Найдите площадь его боковой поверхности. 3.5. Радиус основания цилиндра равен 2дм, площадь боковой поверхности вдвое больше площади основания. Найдите объём цилиндра. 3.6. Найдите объём тела, которое получено при вращении квадрата со стороной 7дм вокруг прямой, соединяющей середины противоположных сторон. 3.7. Высота цилиндра равна 6см, а площадь боковой поверхности вдвое меньше площади его полной поверхности. Найдите объём цилиндра. 3.8. Площадь осевого сечения цилиндра равна 108дм2, а его образующая в три раза меньше диаметра основания. Найдите площадь полной поверхности цилиндра. 3.9. Радиус основания цилиндра равен 8м, площадь боковой поверхности вдвое меньше площади основания. Найдите объём цилиндра. |
| 4. Конус |
4.1. Образующая конуса равна 25м, а диаметр основания - -48м. Найдите объём конуса.
4.2. Высота конуса равна 12дм, а его образующая равна 13дм. Найдите площадь полной поверхности конуса.
4.3. Угол между высотой конуса и образующей равен 300. Найдите площадь полной поверхности конуса, если радиус основания равен 5м.
4.4. Осевое сечение конуса – прямоугольный треугольник. Найдите объём конуса, если радиус основания равен 5 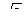 см.
4.5. Найдите объём тела, полученного при вращении прямоугольного треугольника с катетом 3дм и прилежащим углом 300 вокруг меньшего катета.
4.6. Осевое сечение конуса – прямоугольный треугольник. Найдите объём конуса, если радиус основания равен 5 см.
4.5. Найдите объём тела, полученного при вращении прямоугольного треугольника с катетом 3дм и прилежащим углом 300 вокруг меньшего катета.
4.6. Осевое сечение конуса – прямоугольный треугольник. Найдите объём конуса, если радиус основания равен 5 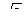 см.
4.7. Найдите объём тела, полученного при вращении прямоугольного треугольника с катетом 3дм и прилежащим углом 300 вокруг меньшего катета. см.
4.7. Найдите объём тела, полученного при вращении прямоугольного треугольника с катетом 3дм и прилежащим углом 300 вокруг меньшего катета.
|
| 4.8. Высота конуса равна 12см, а угол при вершине осевого сечения равен 1200. Найдите площадь полной поверхности конуса. 4.9. Объём конуса с радиусом основания 6м равен 96p м3. Найдите площадь полной поверхности конуса. 4.10. Образующая конуса равна 5см, площадь его боковой поверхности равна 45p см2. Найдите объём конуса. 4.11. Высота конуса равна 8м, объём 24p м3. Найдите площадь полной поверхности конуса. |
| 5. Сфера и шар |
| 5.1. Радиус сечения шара, проведённого на расстоянии 9см от центра, равен 40м. Найдите объём шара. 5.2. Сферу на расстоянии 8м от центра пересекает плоскость. Радиус сечения равен 15м. Найдите площадь сферы. 5.3. Шар с центром в точке О касается плоскости в точке А. Точка В лежит в плоскости касания. Найдите объём шара, если АВ = 21см, ВО = 29см. 5.4. Площадь сечения шара плоскостью, проходящей через его центр, равна 4p дм2. Найдите объём шара. |
| ПРИКЛАДНЫЕ ЗАДАЧИ |
| Многогранники 1. Сколько квадратных метров листовой жести пойдёт на изготовление трубы длиной 4м и диаметром 20см, если на швы необходимо добавить 2,5% площади её боковой поверхности? 2. Металлический куб имеет внешнее ребро 10,2см и массу 514,15г. Толщина стенок равна 0,1см. Найдите плотность металла, из которого сделан куб. 3. Кирпич размером 25´12´6,5см имеет массу 3,51кг. Найдите его плотность. 4. Требуется установить резервуар для воды ёмкостью 10м3 на площадке размером 2,5´1,75м, служащей для него дном. Найдите высоту резервуара. 5. Чугунная труба имеет квадратное сечение, её внешняя ширина 25см, толщина стенок 3см. Какова масса одного погонного метра трубы (плотность чугуна 7,3 г¤см3)? |
| 6. Деревянная плита в форме в форме правильного восьмиугольника со стороной 3,2см и толщиной 0,7см имеет массу 17,3г, Найдите плотность дерева. 7. Вычислите пропускную способность (в кубических метрах за 1ч) водосточной трубы, сечение которой имеет вид равнобедренного треугольника с основанием 1,4м и высотой 1,2м. Скорость течения 2мс. 8. Сечение железнодорожной насыпи имеет вид трапеции с нижним основанием 14м, верхним 8м и высотой 3,2м. Найдите, сколько кубических метров земли приходится на 1км насыпи. |
| Тела вращения 9. Алюминиевый провод диаметром 4мм имеет массу 6,8кг. Найдите длину провода (плотность алюминия 2,6 г¤см3). 10. Какое количество нефти (в тоннах) вмещает цилиндрическая цистерна диаметра 18м и высотой 7м, если плотность нефти равна 0.85 г¤см3? 11. Свинцовая труба (плотность свинца 11,4 г¤см3) с толщиной стенок 4мм имеет внутренний диаметр 13мм. Какова масса трубы, если её длина равна 25м? 12. 25м медной проволоки имеют массу 100,7г. Найдите диаметр проволоки (плотность меди 8,94 г¤см3). 13. Насос, подающий воду в паровой котёл, имеет два водяных цилиндра. Диаметры цилиндров 80мм, а ход поршня 150мм. Чему равна часовая производительность насоса, если каждый поршень делает 50 рабочих ходов в минуту? 14. Сколько бочек длиной 1,5м и диаметром 0,8м нужно , чтобы разлить в них содержимое цистерны длиной 4,5м и диаметром 1,6м? 15. Сколько листового железа требуется для изготовления цилиндрической цистерны объёмом 20м3? 16. Ведро имеет форму усечённого конуса, радиусы оснований которого равны 15см и 10 см, а образующая равна 30см. Сколько килограммов краски нужно взять для того, чтобы покрасить с обеих сторон 100 таких вёдер, если на 1м2 требуется 150г краски? (Толщину стенок вёдер в расчёт не принимать.) |
| 17. Куча щебня имеет коническую форму, радиус основания которой 2м, а образующая 2,5м. Найдите объём кучи щебня. 18. Конусообразная палатка высотой 3,5м с диаметром основания 4м покрыта парусиной. Сколько квадратных метров парусины пошло на палатку? 19. Крыша силосной башни имеет форму конуса. Высота крыши 2м, диаметр башни 6м. найдите поверхность крыши. 20. Стог сена имеет форму цилиндра с коническим верхом. Радиус его основания 2,5м, высота 4м, причём цилиндрическая часть стога имеет высоту 2,2м. Плотность сена 0,03 г¤см3. Определите массу стога сена. 21. Жидкость, налитая в конический сосуд высотой 0,18 м и диаметром основания 0,24 м, переливается в цилиндрический сосуд, диаметр основания которого 0,1 м. Как высоко будет стоять уровень жидкости в сосуде? 22. Диаметр Луны составляет (приблизительно) четвёртую часть диаметра Земли. Сравните объёмы Луны и Земли, считая их шарами. 23. Стаканчик для мороженого конической формы имеет глубину 12см и диаметр верхней части 5см. На него сверху положили две ложки мороженого в виде полушарий диаметром 5см. Переполнит ли мороженое стаканчик, если оно растает? 24. В цилиндрическую мензурку диаметром 2,5см, наполненную водой до некоторого уровня, опускают 4 равных металлических шарика диаметром 1см. На сколько изменится уровень воды в мензурке? 25. Сколько кожи пойдёт на покрышку футбольного мяча радиуса 10см? (На швы добавить 8% от площади поверхности мяча.) |
| 5.3 ДОПОЛНИТЕЛЬНЫЕ ЗАДАНИЯ | |
| 1. Как измерить объём воды в цилиндрической цистерне с помощью вертикального прута? 2. Почему струя воды, текущая из крана, сужается книзу? 3. Одно цилиндрическое бревно вдвое длиннее, но вдвое тоньше другого. Из какого бревна выйдет больше поленьев, если поленья имеют одинаковую массу? | |
| 4. Что бы вы предпочли: съесть арбуз радиуса 15см вчетвером или арбуз радиуса 20см ввосьмером? 5. Комната имеет форму куба. Паук, сидящий в середине ребра, хочет, двигаясь по кратчайшему пути, поймать муху, сидящую в одной из самых удалённых от паука вершин куба. Как должен двигаться паук? 6. Предположим, что муха, разгуливая по 12 рёбрам икосаэдра, ползает по каждому из них по крайней мере один раз. Каков наименьший путь, который должна проделать муха, чтобы побывать на всех рёбрах икосаэдра? Решению задачи может помочь проекция икосаэдра на плоскость.
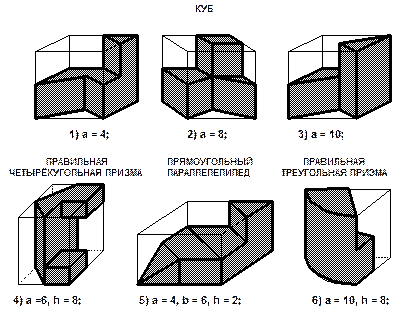
7. Вычислите объём приведённого ниже тела, учитывая размеры исходного многогранника.
| |
|
ПРИЛОЖЕНИЕ | |
|
РАЗВЁРТКИ ФИГУР Развёртка многогранника – совокупность многоугольников, для которых указано, как следует их соединить друг с другом по сторонам и вершинам, чтобы получить данный многогранник, грани которого – эти многоугольники. Развёртку многоугольника можно получить, сделав предварительно один или несколько разрезов её по рёбрам таким образом, чтобы он не распался на отдельные куски, и уложив полученное на плоскость. Аналогично можно уложить на плоскость коническую и цилиндрическую поверхность.
| |
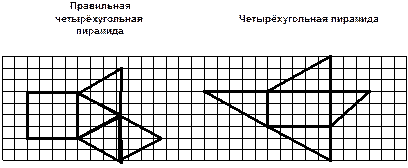

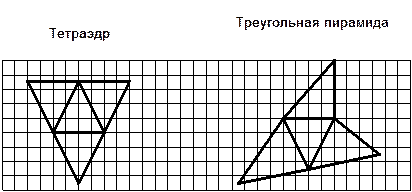
| |
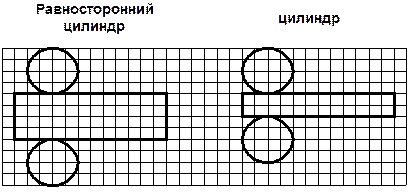
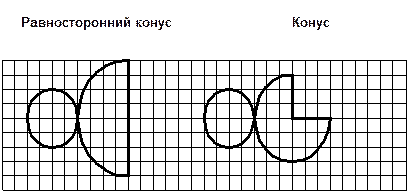
|
Ответы
Задача
рисунок
Ответ
Дата: 2018-12-21, просмотров: 2085.