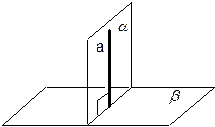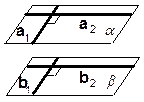
Две пересекающиеся прямые, параллельные соответственно двум перпендикулярным прямым, перпендикулярны:
(a1 || b1, a2 || b2, a1 ^ a2) Þ b1 ^ b2.
ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ
Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой, принадлежащей плоскости и проходящей через точку пересечения.
Признак перпендикулярности прямой и плоскости
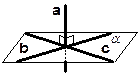
Если прямая перпендикулярна двум пересекающимся прямым данной плоскости, то она перпендикулярна этой плоскости: ( a ^ b и a ^ c) Þ а ^ a.
Свойства перпендикулярности прямой и плоскости
Прямые, перпендикулярные плоскости
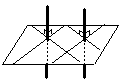
Две прямые, перпендикулярные одной и той же плоскости, параллельны.
Если одна из двух параллельных прямых перпендикулярна данной плоскости, то и другая прямая перпендикулярна этой плоскости
Прямая, перпендикулярная плоскостям
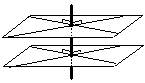
Прямая, перпендикулярная одной из двух параллельных плоскостей, перпендикулярна и другой плоскости.
Две плоскости, перпендикулярные одной и той же прямой, параллельны.
|
ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ Пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым. | ||||
|
| ||||
|
Признак перпендикулярности плоскостей | ||||
|
|
Плоскости перпендикулярны, если одна из них содержит перпендикуляр к другой плоскости: (a Ì a, a ^ b) Þ a ^ b. | |||
|
Свойство перпендикулярных плоскостей | ||||
|
|
Если плоскости перпендикулярны, то прямая, лежащая в одной из них и перпендикулярная линии пересечения плоскостей, перпендикулярна другой плоскости: (a ^ b, a Ì a, a ^ b) Þ a ^ b. | |||
|
ПЕРПЕНДИКУЛЯР И НАКЛОННЫЕ | ||||
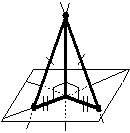
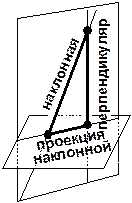 Перпендикуляр короче любой наклонной, проведенной к плоскости из той же точки.
Перпендикуляр короче любой наклонной, проведенной к плоскости из той же точки.
|
У равных наклонных, проведенной к плоскости из одной точки, проекции равны. Справедливо и обратное: если у двух наклонных, проведенных из одной точки, проекции равны, то равны и наклонные. | 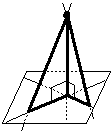 Из двух наклонных, проведенных из одной точки, больше та, у которой проекция больше.
Справедливо и обратное.
Из двух наклонных, проведенных из одной точки, больше та, у которой проекция больше.
Справедливо и обратное.
| ||
|
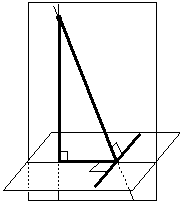
Теорема о трёх перпендикулярах | ||||
|
|
Теорема о трёх Перпендикулярах. (содержит два утверждения: прямое и обратное) Если прямая, лежащая в плоскости и проходящая через основание наклонной, перпендикулярна проекции наклонной, то она перпендикулярна и самой наклонной. Если прямая, лежащая в плоскости и проходящая через основание наклонной, перпендикулярна наклонной, то она перпендикулярна и проекции наклонной. | |||
|
СКРЕЩИВАЮЩИЕСЯ ПРЯМЫЕ Так называются прямые, которые не лежат в одной плоскости, то есть не параллельны и не пересекаются. | |
Дата: 2018-12-21, просмотров: 970. |
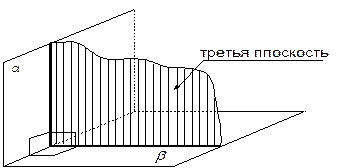 a ^ b
a ^ b