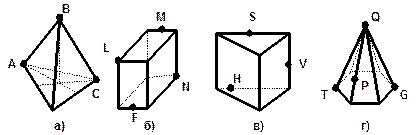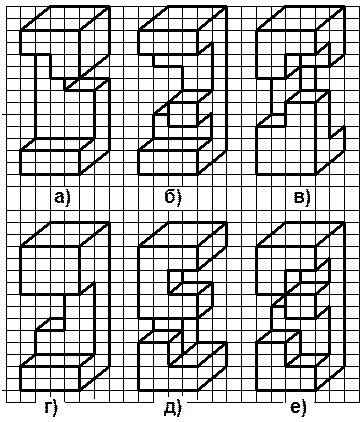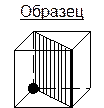
Найдите линии пересечения этой плоскости с гранями и заштрихуйте полученный многоугольник.
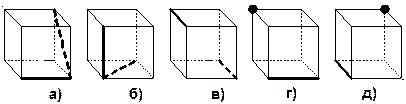
9. Треугольники АВС и АВD лежат в разных плоскостях. Точки А1 и В1 - середины отрезков АС и ВС. Докажите, что прямая А1В1 параллельна плоскости ABD.
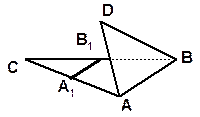
| 10. Точки А, В, С, D не лежат в одной плоскости. Точки E,F,H–соответственно середины отрезков АВ, АС,АD. Докажите, что плоскости ВСD и EFH параллельны. |
| ||
| 11. Даны две параллельные плоскости. Через точки А и В одной из них проведены параллельные прямые, пересекающие вторую плоскость в точках А1 и В1. Докажите, что четырёхугольник АВВ1А1 – параллелограмм. | 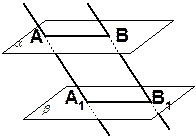
| ||
| 12. KLMN - тетраэдр (все грани – равносторонние треугольники). | |||
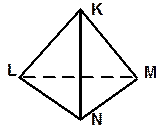
| а) Постройте сечение этого тетраэдра плоскостью, проходящей через ребро KL и точку А-середину ребра NM; б) Докажите, что плоскость, проходящая через середины Е, О, и F отрезков LM, MA и МК, параллельна плоскости LKA. | ||
| 13. Стороны АВ и ВС параллелограмма АВСD пересекают плоскость 14. Докажите, что если данная прямая параллельна прямой, по которой пересекаются две плоскости, и не лежит в этих плоскостях, то она параллельна этим плоскостям. 15. Основание АВ трапеции АВСD параллельно плоскости | |||
16. Докажите, что если три плоскости, не проходящие через одну прямую, попарно пересекаются, то прямые, по которым они пересекаются, либо параллельны, либо имеют общую точку.
17. В пространственном четырёхугольнике АВСD стороны АВ и CD равны. Докажите, что прямые АВ и CD образуют равные углы с прямой, проходящей через середины отрезков ВС и AD.
18. Докажите, что плоскости 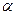 и и 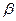 параллельны, если две пересекающиеся прямые m и n плоскости параллельны, если две пересекающиеся прямые m и n плоскости 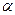 параллельны плоскости параллельны плоскости 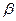 . .
|
|
ПРОЧИТАЙТЕ УСЛОВИЕ ЗАДАЧ И РАЗБЕРИТЕ ИХ РЕШЕНИЕ | ||||
| 1. Через концы отрезка АВ и его середину М проведены параллельные прямые, пересекающие некоторую плоскость в точках А1, В1 и М1. Найдите длину отрезка ММ1, если АА1 = 3,6 дм, ВВ1 = 4,8 дм. | ||||
Дано:
АВ, 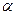 ;
М ;
М 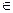 АВ;
АМ= МВ;
А1, М1, В1 АВ;
АМ= МВ;
А1, М1, В1 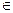 a;
АА1| | DD1| | ММ1;
АА1= 3,6см;
ВВ1= 4,8см.
Найти: ММ1. a;
АА1| | DD1| | ММ1;
АА1= 3,6см;
ВВ1= 4,8см.
Найти: ММ1.
|
| Решение:
1) Если АА1||ВВ1||ММ1- то эти отрезки лежат в одной плоскости b(по свойству параллельных прямых).
b  a=А1В1. a=А1В1.
| ||
| 2) По теореме Фалеса М1 - середина АВ, тогда ММ1 - средняя линия трапеции АА1В1ВÞ по свойству средней линии трапеции ММ1= Ответ: ММ1 = 4,2см.
| ||||
| Примерный план решения задач первого типа 1. Провести плоскость через: две параллельные прямые; две пересекающиеся прямые; треугольник, трапецию. 2. Применяя теорему Фалеса, признак параллельности прямой и плоскости доказать, что дана средняя линия треугольника (трапеции). 3. Используя свойство средней линии треугольника (трапеции) найти неизвестные величины. 2. Точки М, Н, К, Р–середины соответственно отрезков А D , DС, ВС, АВ. Найдите периметр четырёхугольника МНКР, если МР = 8дм., АС =32дм. | ||||
| Дано: [АD],[DС],[ВС],[АВ]; МÎАD, АМ= МD; НÎDС, DН=НС; РÎАВ, АР= РВ; КÎ ВС, ВК= КС; МР= 8дм., АС= 32дм. Найти: РМНКР. | 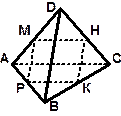
| Решение: 1) АВСD пространственный четырёхугольник (его вершины не лежат в одной плоскости) и М, Н, К, Р- середины его сторон (кроме АС). | ||
| 2) РМ - средняя линия DАВD (по условию) ÞРМ|| ВD; НК - средняя линия DСDВÞНК|| ВD, значит по признаку параллельности прямых РМ|| НК, тогда четырёхугольник РМНК лежит в одной плоскости. МН - средняя линия DАDС и РК- средняя линия DАВСÞМН|| АС и РК||АС, тогда МН|| РК, значит РМНК – параллелограмм 3) РМНКР = 2(РМ+МН). По свойству средней линии треугольника МН= Ответ: РМНКР.=48дм.
| ||||
Примерный план решения задач второго типа 1.Дан пространственный четырёхугольник (его вершины не лежат в одной плоскости). Указать точки, которые являются серединами его сторон. 2. Применяя признак параллельности прямых в пространстве и свойство средней линии треугольника, доказать, что фигура, лежащая внутри пространственного четырёхугольника – параллелограмм. 3. Применяя свойства средней линии треугольника и параллелограмма, найти неизвестные величины. 3. Дан треугольник АВС. Плоскость, параллельная прямой АВ, пересекает сторону АС этого треугольника в точке А1, а сторону ВС – в точке В1. Найдите длину отрезкаА1В1, если В1С = 10см., АВ/ВС = 4/5. | ||
Дано:
DАВС, a||АВ;
a  АС = А1;
a АС = А1;
a  ВС = В1;
В1С = 10см.;
АВ/ВС = 4/5.
Найти: А1В1. ВС = В1;
В1С = 10см.;
АВ/ВС = 4/5.
Найти: А1В1.
| 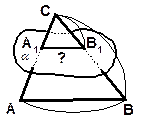
| Решение:
1) Пусть DАВС лежит в плоскости g, тогда g 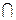 a = А1В1.
А1В1Îa и a||АВÞ А1В1||АВ (по признаку параллельности прямой и плоскости). a = А1В1.
А1В1Îa и a||АВÞ А1В1||АВ (по признаку параллельности прямой и плоскости).
|
| 2) DАВС ¥ DА1В1С по второму признаку подобия треугольников (ÐАСВ – общий, ÐСВ1А1 = ÐСВА как односторонние углы при параллельных прямых АВ и А1В1). 3) | ||
| Примерный план решения задач третьего, Четвёртого и пятого типов 1. Провести плоскость через: треугольник, две пересекающиеся прямые. Указать линию (линии) пересечения плоскостей. Доказать параллельность необходимых сторон. 2. Записать подобные треугольники, признак, обоснование. 3. Записать пропорциональность сторон подобных треугольников. Подставить известные величины и найти неизвестные. | ||
|
РИСУНКИ К ЗАДАЧАМ | ||
|
Примечание: дугой обозначены известные, неизвестные величины знаком "?". | ||
| 2.4 ЗАДАЧИ |
| 1. Точка С лежит на отрезке АВ. Через точку А проведена плоскость , а через точки В и С – параллельные прямые, пересекающие плоскость соответственно в точках В1 и С1. Найти длину отрезка СС1, если точка С – середина отрезка АВ и ВВ1=7м. 2. Точка М, Н, Р и К – середины соответственно отрезков АD, DС, АВ и ВС; РК || МН. Найти периметр четырехугольника МНКР, если АС=8дм., ВD=10дм. 3. На сторонах АВ и АС треугольника АВС взяты соответственно точки D и Е так, что DЕ = 5см., а ВD / DА =2/3. Плоскость a проходит через точки В и С и параллельна отрезку ДЕ. Найдите длину отрезка ВС. 4. Точка А - середина отрезка МР, а точки В, С, D лежат соответственно на отрезках КР, КН, МН. ВС || РН, АD || РН, АВ || СD. Найдите РН, если АВ=4дм., а периметр четырехугольника АВСD равен 28 дм. 5.Плоскоть, параллельная основаниям трапеции, пересекает стороны АВ и СD в точках М и К соответственно, АD=10м., ВС=6м. Найти МК, если М-середина отрезка АВ. 6. Точки М, N, Q и Р - середины отрезков DВ и DС, АС и АВ. Найти периметр четырехугольника MNQP, если АD=12мм., ВС=14мм. 7. Точка С лежит на отрезке АВ. Через точку А проведена плоскость, а через точки В и С- параллельные прямые, пересекающие эту плоскость соответственно в точках В1 и С1. Найдите длину отрезка СС1, если АC/СВ=3/2 и ВВ1=20м. 8. Дан треугольник АВС. Плоскость, параллельная прямой АВ, пересекает сторону АС в точке К, а сторону ВС - в точке М. Найти длину отрезка АВ, если длина КС =12дм., АС=24дм., КМ=9дм. 9. Параллельные плоскости a и b пересекают сторону АВ угла ВАС соответственно в точках А1 и А2 , а сторону АС этого угла – соответственно в точках В1 и В2. Найти АА2 и АВ2, если А1А2=2А1А, А1А2=12м., АВ1=5м. 10.Точки D, С, В лежат соответственно на отрезках МК, МН, РН. Точка А – середина отрезка РК, АВ||СD, ВС||АD, ВС||РМ, СD||НК. Найти РМ и НК, если СD=16мм., ВС=8мм. 11.Через концы отрезка АВ и его середину М проведены параллельные прямые, пересекающие некоторую плоскость в точках А1, В1 и M1. Найдите длину отрезка MM1, если AA1=5 см, BB1=7 см. |
 12. Через точку К проведены две прямые a и b, пересекающие две параллельные плоскости a и b: первую в точках А1 и А2, вторую в точках В1 и В2 соответственно. Вычислить КА1 и КВ2, если:
а) А1А2/В1В2=3/4, А1В1=7дм, КА2=12дм;
б) А1А2/ В1В2=1/6, А2В2=3см, В1К=12см.
Точка К не лежит между плоскостями a и b.
13.В треугольнике АВС АВ=15м., АС=24м. Через точку М на стороне АВ, находящейся на расстоянии 10м от точки А, проведена плоскость, параллельная прямой АС и пересекающая сторону ВС в точке К. Найдите длину отрезка МК.
14. Плоскость, параллельная стороне АВ треугольника АВС, пересекает его стороны в точках М и К. Найти АВ, если М- середина стороны АС и МК=10мм.
15. Параллельные плоскости a и b пересекают стороны угла АВС в точках А1, С1, А2, С2 соответственно. Найти ВС1, если А1В/А1А2=1/3, ВС2=12мм.
16. Точка К лежит между параллельными плоскостями a и b. Прямые а и b, проходящие через точку К, пересекают плоскость a в точках А1 и В1, а плоскость b в точках А2 и В2 соответственно. Найти КВ1, если:
а) А1К/А1А2=1/3, В1В2=15м.;
б) В1А1/В2А2=4/6, КВ2=8дм;
в) А2К/А1А2=2/5, В1В2=20см;
г) КВ2/А1В1=1/6, А2В2=2мм.
17. Треугольник АРD и трапеция АВСD имеют общую сторону АD и лежат в разных плоскостях. Через основание ВС трапеции и середину отрезка РD – точку К проведена плоскость, которая пересекает прямую АР в точке М. Найти МК, если АД=10м.
18. Через точку А стороны КМ треугольника КМР проведена плоскость, параллельная прямой МР. Вычислить длину отрезков, на которые делится эта плоскость сторону КР, если МК=10см., МА=6см, КР=15дм.
19. Треугольники АВС и DВС не лежат в одной плоскости и имеют общую сторону; точки М, Н, К- середины соответственно сторон ВD, DС, АС. Отрезок АВ пересекает плоскость МКН в точке Р. Найти РК, если ВС=8м.
20. Параллельные плоскости a и b пересекают сторону АВ угла ВАС соответственно в точках А1 и А2, и сторону АС этого угла - соответственно в точках В1 и В2. Найти А2В2 и АА2, если А1В1=18см., АА1=24см., АА2=3/2А1А2. 12. Через точку К проведены две прямые a и b, пересекающие две параллельные плоскости a и b: первую в точках А1 и А2, вторую в точках В1 и В2 соответственно. Вычислить КА1 и КВ2, если:
а) А1А2/В1В2=3/4, А1В1=7дм, КА2=12дм;
б) А1А2/ В1В2=1/6, А2В2=3см, В1К=12см.
Точка К не лежит между плоскостями a и b.
13.В треугольнике АВС АВ=15м., АС=24м. Через точку М на стороне АВ, находящейся на расстоянии 10м от точки А, проведена плоскость, параллельная прямой АС и пересекающая сторону ВС в точке К. Найдите длину отрезка МК.
14. Плоскость, параллельная стороне АВ треугольника АВС, пересекает его стороны в точках М и К. Найти АВ, если М- середина стороны АС и МК=10мм.
15. Параллельные плоскости a и b пересекают стороны угла АВС в точках А1, С1, А2, С2 соответственно. Найти ВС1, если А1В/А1А2=1/3, ВС2=12мм.
16. Точка К лежит между параллельными плоскостями a и b. Прямые а и b, проходящие через точку К, пересекают плоскость a в точках А1 и В1, а плоскость b в точках А2 и В2 соответственно. Найти КВ1, если:
а) А1К/А1А2=1/3, В1В2=15м.;
б) В1А1/В2А2=4/6, КВ2=8дм;
в) А2К/А1А2=2/5, В1В2=20см;
г) КВ2/А1В1=1/6, А2В2=2мм.
17. Треугольник АРD и трапеция АВСD имеют общую сторону АD и лежат в разных плоскостях. Через основание ВС трапеции и середину отрезка РD – точку К проведена плоскость, которая пересекает прямую АР в точке М. Найти МК, если АД=10м.
18. Через точку А стороны КМ треугольника КМР проведена плоскость, параллельная прямой МР. Вычислить длину отрезков, на которые делится эта плоскость сторону КР, если МК=10см., МА=6см, КР=15дм.
19. Треугольники АВС и DВС не лежат в одной плоскости и имеют общую сторону; точки М, Н, К- середины соответственно сторон ВD, DС, АС. Отрезок АВ пересекает плоскость МКН в точке Р. Найти РК, если ВС=8м.
20. Параллельные плоскости a и b пересекают сторону АВ угла ВАС соответственно в точках А1 и А2, и сторону АС этого угла - соответственно в точках В1 и В2. Найти А2В2 и АА2, если А1В1=18см., АА1=24см., АА2=3/2А1А2.
|
|
ДОПОЛНИТЕЛЬНЫЕ ЗАДАНИЯ. | |||||||
|
1. Продолжение отрезка ВС пересекает плоскость
|
| ||||||
| 2. На рисунке изображены параллельные плоскости | |||||||
|
|
Скопируйте рисунок и изобразите на нём точку В, принадлежащую плоскости | ||||||
| 3. Зарисуйте примеры конструкций, которые спереди и слева имеют следующий вид. (В конструкции используйте только кубики).
4. На рисунке изображены геометрические тела, на поверхности которых отмечены точки. Назовите эти фигуры, нарисуйте развёртки поверхностей этих тел и покажите на них соответствующие точки. Примеры развёрток смотрите в приложении.
| |||||||
| 5. Постройте развёртку поверхности куба: а) ребро которого равно 35мм; б) диагональ грани которого равна 4см. Склейте эти модели ( припуски удобней делать на боковых гранях). 6. Рассмотрите набор деревянных брусков. Выясните можно ли составить каждый брусок из кубиков с ребром а= 2 клетки? Если да, то сколько кубиков понадобится для работы?
7. Перерисуйте из приложения развертку: правильной треугольной призмы; правильной пятиугольной призмы; наклонного параллелепипеда. Обозначьте вершины у каждой фигуры и перечислите: а) все параллельные ребра (нарисуйте их одним цветом); б) все диагонали боковых граней и оснований (нарисуйте их другим цветом); | |||||||
| в) все диагонали призмы и параллелепипеда. Для выполнения этого задания развёртки фигур необходимо увеличить и склеить (припуски удобней делать на боковых гранях).
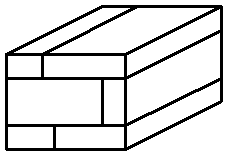
8. Сколько прямоугольных параллелепипедов изображено на рисунке?
9. Туго натянутая нить последовательно закреплена в точках | |||||||
|
| 1, 2, 3, 4, 5 и 6, расположенных на стержнях SA, SB и SC, которые не принадлежат одной плоскости. Скопируйте рисунок, отметьте и обозначьте точки, в которых отрезки нити соприкасаются | ||||||
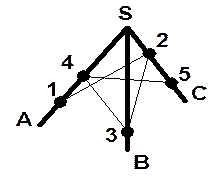
| 10. Туго натянутая нить последовательно закреплена в точках | |||||||
|
| 1, 2, 3, 4, и 5, расположенных на стержнях SA, SB и SC, которые не принадлежат одной плоскости. Скопируйте рисунок, отметьте и обозначьте точки, в которых отрезки нити соприкасаются. | ||||||
|
ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ | |||||||
|
ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ Две прямые называются перпендикулярными, если они пересекаются под прямым углом. | |||||||
Дата: 2018-12-21, просмотров: 1845. | |||||||
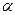 .
.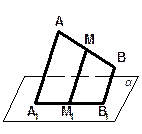
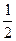 (АА1+ВВ1) =
(АА1+ВВ1) = 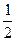 АС=
АС= 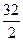 =16(дм.). РМНКР.=2(8+16)=48(дм.).
=16(дм.). РМНКР.=2(8+16)=48(дм.).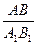 =
= 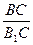 =
= 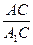 ;
; 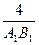 =
= 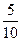 ; А1В1=
; А1В1= 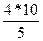 =8. Ответ: 8см.
=8. Ответ: 8см. 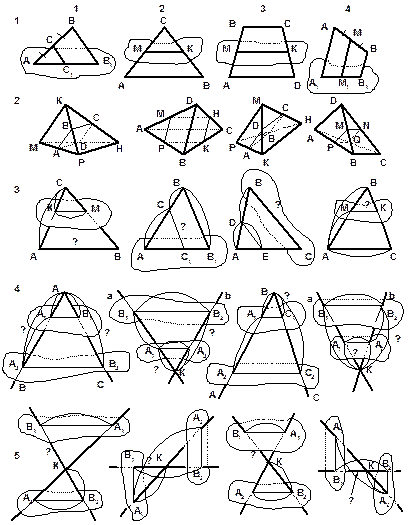
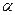 . Скопируйте рисунок и изобразите отрезки АС и ВD. Определите, пересекаются ли эти отрезки? Ответ обоснуйте.
. Скопируйте рисунок и изобразите отрезки АС и ВD. Определите, пересекаются ли эти отрезки? Ответ обоснуйте.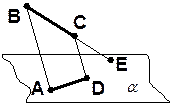
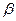 . Точка А принадлежит плоскости
. Точка А принадлежит плоскости 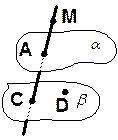
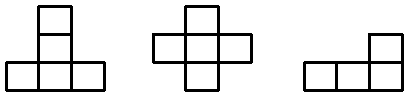 а) б) в)
а) б) в)