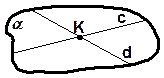Найдите сторону треугольника

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

R = 5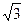

R = 6

r = 4

R =

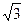
r =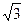

ПОДОБИЕ ТРЕУГОЛЬНИКОВ

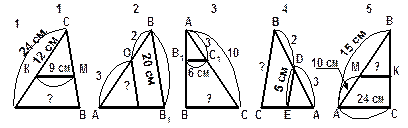
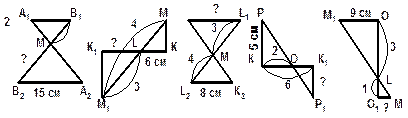
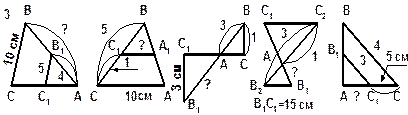ПРИМЕРНЫЙ ПЛАН РЕШЕНИЯ 1.Записать подобные треугольники и указать признак подобия (обосновать). 2.Из подобия треугольников записать пропорциональность соответствующих сторон. 3. Подставить известные величины в пропорцию и найти неизвестную сторону (обозначенной знаком "?").

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК

6. Найдите гипотенузу.

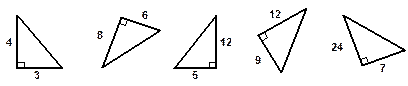2. Найдите неизвестный катет.

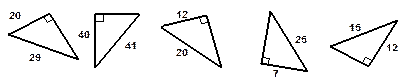3. Найдите неизвестную сторону прямоугольного треугольника .

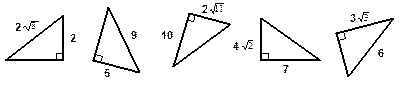4. Найдите неизвестную сторону прямоугольного треугольника если:

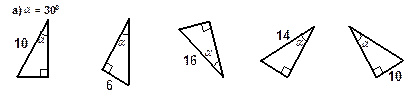
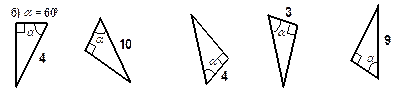
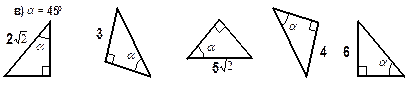
ЧЕТЫРЁХУГОЛЬНИК

Найдите периметр.

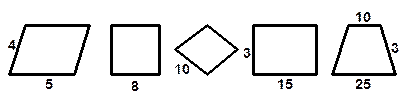
Найдите площадь.

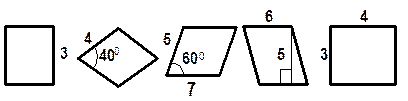
Найдите радиус описанной R (вписанной r ) окружности.

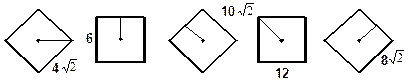4. Найдите сторону квадрата.

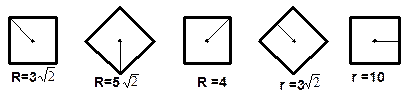
Найдите среднюю линию трапеции.

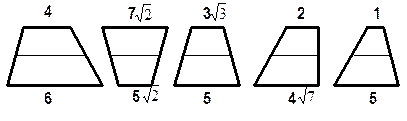
ДОПОЛНИТЕЛЬНЫЕ ЗАДАНИЯ

1. Сколько всего треугольников изображено на рисунке.

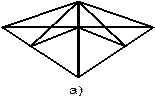
2. Найдите площадь заштрихованной фигуры.

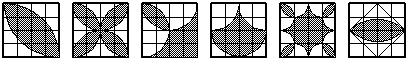
а) б) в) г) д) е)

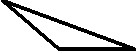
3. Разрежьте тупоугольный треугольник на остроугольные треугольники.

4. Разрежьте остроугольный равнобедренный треугольник на четыре одинаковых равнобедренных треугольника, подобных исходному.

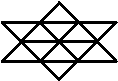
5. Отец красавицы Лолиты, живший в древней Индии, назойливым женихам давал несколько заданий. И лишь тот, кто выполнял эти задания, мог претендовать на ее руку. Вот одно из них: скажи, сколько треугольников нарисовано на полу в центральном зале?

6. На берегу священной реки Ганг жил знаменитый брахман Радж. Он обнес свой замок глубоким рвом, наполненным водой. И только тот мог попасть в замок, кто с помощью двух дощечек, длина которых меньше ширины рва, не замочив ног, переходил ров. Попробуй и ты побывать в гостях у Раджи.

СТЕРЕОМЕТРИЯ

Так называется раздел геометрии, в котором изучаются фигуры

в пространстве.

ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ

Способы задания точки

Точка в пространстве однозначно определяется:

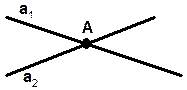
двумя пересекающимися

прямыми;

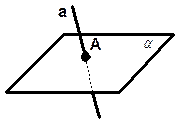пересекающимися прямой и плоскостью;

тремя попарно пересекающимися плоскостями, если прямые пересечения плоскостей пересекаются.

Способы задания прямой

Прямая в пространстве однозначно определяется:

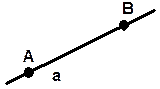
двумя точками;

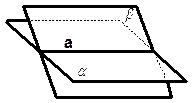двумя пересекающимися плоскостями.

Способы задания плоскости

Плоскость в пространстве однозначно определяется:

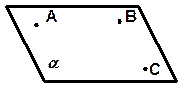тремя точками, не лежащими на одной прямой;

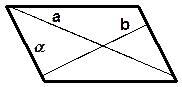двумя пересекающимися прямыми;

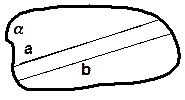двумя параллельными прямыми;

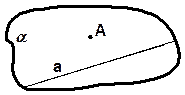прямой и точкой, не лежащей на ней.

АКСИОМЫ СТЕРЕОМЕТРИИ
С₁ A Î a, M Ï a	Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.
С₂ 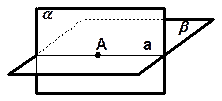a b = а	Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.

C₃

Если две различные прямые имеют общую точку, то через них можно провести плоскость и притом только одну.

Дата: 2018-12-21, просмотров: 642.

⇐ Предыдущая 1 2 345 6 7 8 9 10 Следующая ⇒