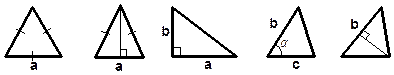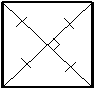
Диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.
Все свойства параллелограмма верны для квадрата.
ТРАПЕЦИЯ
Так называется четырехугольник, у которого две стороны параллельны (основания), а две другие – не параллельны (боковые стороны).

Свойства трапеции
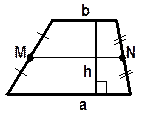
Средняя линия параллельна основаниям, равна их полусумме и делит любой отрезок с концами, лежащими на прямых, содержащих основания, (например, высоту трапеции) пополам:
MN || a, MN || b, MN = 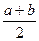 .
.
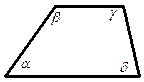
Сумма углов, принадлежащих к любой боковой стороне, равна 1800:
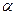 +
+ 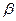 = 1800,
= 1800,
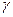 +
+ 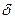 = 1800.
= 1800.
ОКРУЖНОСТЬ
Так называется фигура, которая состоит из всех точек плоскости, равноудалённых от данной точки. Эта точка называется центром окружности
Часть плоскости, ограниченная окружностью, называется
Кругом
|
Прямые и отрезки, связанные с окружностью | |
|
| |
|
Углы, связанные с окружностью Угловая мера дуги окружности | |

| Центральным углом в окружности называется плоский угол с вершиной в её центре. Дугой окружности называется часть окружности, расположенная внутри плоского угла соответствующая центральному углу. Угловой мерой дуги окружности является центральный угол, который опирается на эту дугу. |
|
Радианная мера угла Угол в один радиан равен центральному углу, опирающемуся на дугу, длина которой равна радиусу окружности | |
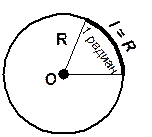
| Радианной мерой угла называется отношение длины соответствующей дуги к радиусу окружности.
1 радиан » 57017¢ 45¢¢,
10 =  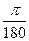 радиан.
p радиан -1800,
p радиан.
p радиан -1800,
p  3,14 радиан. 3,14 радиан.
|
|
ОСНОВНЫЕ ФОРМУЛЫ | |||
|
Наименование |
Формулы для вычисления | ||
| Периметра | Площади | Радиуса | |
| 1 | 2 | 3 | 4 |
Треугольник
1. Произвольный
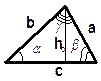 2. Равносторонний
(правильный)
2. Равносторонний
(правильный)
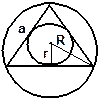 3. Прямоугольный
3. Прямоугольный
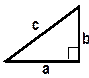
| P =a+b+c P = 3×a P =a+b+ с | S =  hC × c, S= hC × c, S=  b × c × sin a ,
Формула Герона:
S= b × c × sin a ,
Формула Герона:
S= 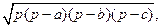 где p = где p = 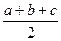 .
S = p × r; S = .
S = p × r; S = 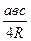 S =
S = 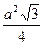 S =
S = 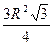 ;
S = 3r2 ;
S = 3r2 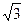 S =
S =  a × b a × b
|
a=R 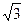 a=2r
a=2r 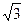 R=
R= 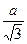 ,
r= ,
r= 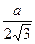 r =
r =  R, R=2r R, R=2r
|
| 1 | 2 | 3 | 4 |
Четырёхугольник
1. Параллелограмм
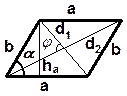 2. Ромб
2. Ромб
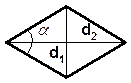 3. Прямоугольник 3. Прямоугольник
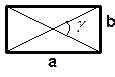 4. Квадрат
4. Квадрат
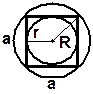 5. Трапеция
5. Трапеция
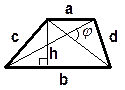
| P = 2(a +b) P = 4a P = 2(a +b) P = 4a P=a+b+c+d |
S = a × b × sin a ,
S = a × h a ,
S =  d1d2 sin j
S = a2 × sin a ,
S = d1d2 sin j
S = a2 × sin a ,
S =  d 1 × d 2
S = a×b
S = d 1 × d 2
S = a×b
S =  d2sin g
S = a2
S = d2sin g
S = a2
S =  d2
S = d2
S =  (a + b)h
S = (a + b)h
S =  d1d2sin j d1d2sin j
|
a=R 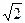 a=2 × r
R= r a=2 × r
R= r 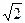 r=
r= 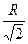
|
|
Площадь круга и его частей | ||
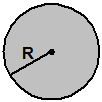 Площадь круга:
S = p R 2 .
Площадь круга:
S = p R 2 .
|
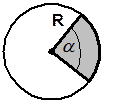 Площадь сектора:
S =
Площадь сектора:
S =  a R 2
(угол в радианах). a R 2
(угол в радианах).
|
 Площадь сегмента:
S =
Площадь сегмента:
S =  ( a – sin a ) R 2
(угол a в радианах). ( a – sin a ) R 2
(угол a в радианах).
|
|
Длина дуги и окружности | |
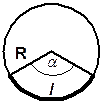 Длина дуги:
l = a R
(угол a в радианах).
Длина дуги:
l = a R
(угол a в радианах).
| 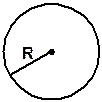 Длина окружности:
L = 2 p R .
Длина окружности:
L = 2 p R .
|
|
ЗАДАЧИ ТРЕУГОЛЬНИК | ||||||||||
|
Найти неизвестный угол в треугольнике.
| ||||||||||
| a = 600,b=450 Найти: g | a = 350, g= 200 Найти: b | Найти: a | a = 400 Найти: b | a = 800 Найти: b,g | ||||||
|
Найти периметр треугольника.
| ||||||||||
| a = 3, b = 4 | a = 6 | a = 4, b = 3,5 | a = 4, b = 5, c = 6 | с = 6 | ||||||
|
Найдите площадь треугольника.
| ||||||||||
| а = 4 | а = 10,ha=5 | а = 2,5, b= 4 | с = 5, b=6,a=450 | b = 8, hb =6 | ||||||
|
Найдите радиус описанной R (вписанной r ) окружности.
| ||||||||||
| а = 6 | а = 8 | а = 4 | а = 2 | а = 7 | ||||||
Дата: 2018-12-21, просмотров: 824. | ||||||||||
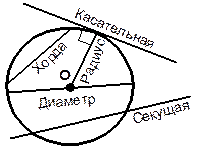
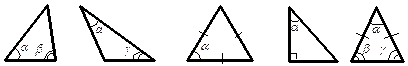
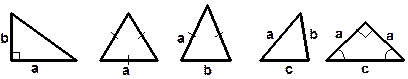
 , а=6
, а=6