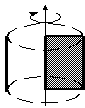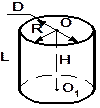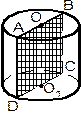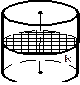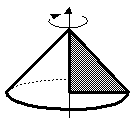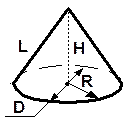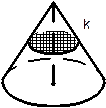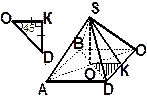
Решение:
1) Ребро SD найдем из  SKD, по теореме Пифагора SD2 = SK2 + KD2 (отметим, что
SKD, по теореме Пифагора SD2 = SK2 + KD2 (отметим, что  DSC равнобедренный, т.к. SABCD – правильная пирамида,
DSC равнобедренный, т.к. SABCD – правильная пирамида,
SK является медианой и высотой), SK =15 см, KD -?
2) Найдем KD. Для этого рассмотрим  OKD, он прямоугольный и равнобедренный (SK
OKD, он прямоугольный и равнобедренный (SK 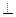 CD
CD 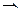 OK
OK 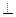 SD, ОК – радиус вписанной окружности в основание), ОК = DC/2 и KD =DC/2.
SD, ОК – радиус вписанной окружности в основание), ОК = DC/2 и KD =DC/2.
Если ОК = KD, то найдем ОК из 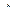 SOK по теореме Пифагора SK2 = SО2 – SO2 = 152 – 122 =81, ОК =
SOK по теореме Пифагора SK2 = SО2 – SO2 = 152 – 122 =81, ОК = 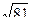 = 9 (см)
= 9 (см) 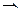 KD = 9 см.
KD = 9 см.
Тогда SD2 = 152 + 92 =225 +81 = 306, SD = 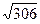 = 3
= 3 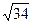 (см).
(см).
Ответ: SD = 3 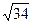 см.
см.
В правильной треугольной пирамиде сторона основания равна 12 м, а апофема боковой грани 8 м. Найдите боковое ребро пирамиды и высоту.
Дано:
FKLV –
правильная
пирамида.
а = KL = 12 м
l = FN= 8 м.
Найти: FK, FО.
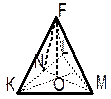
Решение:
1) Боковое ребро FK найдем из прямоугольного  FNK, по теореме Пифагора FK2 = FN2 + NK2 = 82 + 62 = 100, FK=
FNK, по теореме Пифагора FK2 = FN2 + NK2 = 82 + 62 = 100, FK= 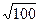 =10(м).
=10(м).
( NK = KL : 2 т.к. FN – высота и медиана  KFL)
KFL)
2) FО -? Из прямоугольного  NOF по теореме Пифагора FN2 = FO2 + NO2
NOF по теореме Пифагора FN2 = FO2 + NO2  FO2 = FN2 – NO2, FN= 8м.
FO2 = FN2 – NO2, FN= 8м.
3) NO - ? NO = r – радиус вписанной окружности в  KLM
KLM 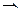
NO = 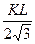 =
= 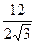 =
= 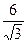 =2
=2 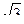 (м).
(м).
Тогда FO2 = 82 – (2 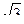 )2 = 64-12 =52, FO =
)2 = 64-12 =52, FO = 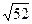 =
= 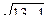 = 2
= 2 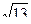 (м).
(м).
Ответ: FK = 10м, FO =2 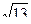 м.
м.
В основании пирамиды лежит прямоугольный треугольник, гипотенуза которого равна 15 дм, а один из катетов – 9 дм. Найдите площадь сечения, проведенного через середину высоты пирамиды, параллельно ее основанию.
Дано:
SABC – пирамида.
 АВС =900.
АВС =900.
АС = 15 дм, ВС =9 дм.
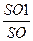 =
= 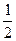
Найти: S 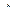 А1В1С1
А1В1С1
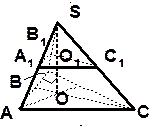
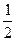 , известно, что
, известно, что
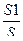 = k2
= k2 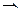 S
S  А1В1С1/ S
А1В1С1/ S  АВС =
АВС = 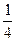 . S
. S 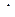 А1В1С1 = S
А1В1С1 = S 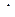 АВС/ 4.
АВС/ 4.
2) S 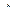 АВС -?
АВС -? 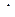 АВС – прямоугольный
АВС – прямоугольный 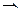 S
S 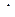 А1В1С1 =
А1В1С1 = 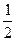 АВ× ВС, АВ -? По теореме Пифагора АС2 =АВ2 + ВС2
АВ× ВС, АВ -? По теореме Пифагора АС2 =АВ2 + ВС2 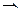 АВ2= АС2 –ВС2 = 152 –92 =144,
АВ2= АС2 –ВС2 = 152 –92 =144,
АВ = 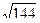 =12 (дм). S
=12 (дм). S 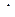 А1В1С1 =
А1В1С1 = 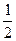
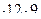 =54 (дм).
=54 (дм).
Ответ: S  А1В1С1 =
А1В1С1 = 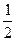
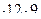 =54 дм.
=54 дм.
| РИСУНКИ К ЗАДАЧАМ (призма) |
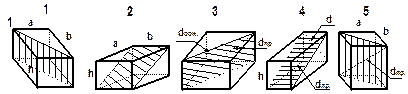
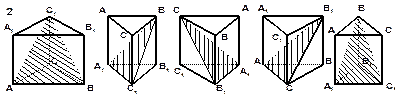

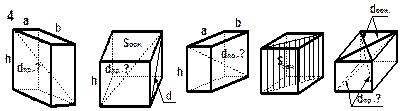
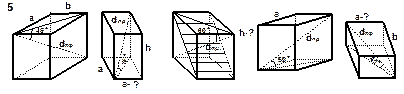 Примечание: а, b -стороны основания; h -высота;
S осн. -площадь основания;
S сеч. -площадь сечения;
d пр.(осн.) -диагональ призмы (основания).
Примечание: а, b -стороны основания; h -высота;
S осн. -площадь основания;
S сеч. -площадь сечения;
d пр.(осн.) -диагональ призмы (основания).
|
| РИСУНКИ К ЗАДАЧАМ (пирамида) |
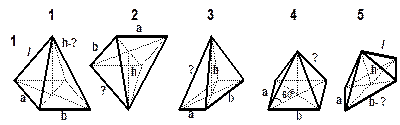
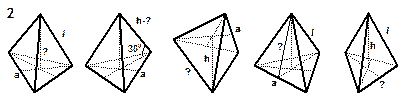
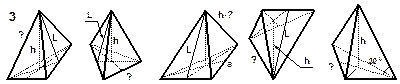
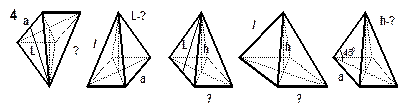
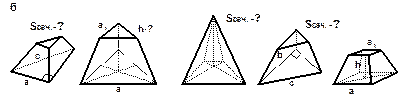 Примечание: а, b, с – стороны основания;
h – высота;
L – апофема;
l – длина бокового ребра;
S сеч. – площадь сечения. Примечание: а, b, с – стороны основания;
h – высота;
L – апофема;
l – длина бокового ребра;
S сеч. – площадь сечения.
|
| 3.2 ЗАДАЧИ (призма) |
1. Дана прямая призма, в основании которой лежит прямоугольник. Диагональ призмы 15м. Высота призмы равна 7м. Найдите площадь диагонального сечения.
2. В правильной треугольной призме АВСА1В1С1 проведено сечение через вершину С1 и ребро АВ. найдите периметр сечения, если сторона основания равна 24см., а боковое ребро- 10см.
3. Диагональное сечение правильной четырёхугольной призмы, у которой сторона основания равна 10см. и высота 12см., разбивает её на две треугольные призмы. Найдите площади боковых поверхностей треугольных призм.
4. В правильной четырёхугольной призме площадь основания равна 144дм2, а высота 14дм. Найдите диагональ призмы.
5. Определите диагональ прямоугольного параллелепипеда по трём его измерениям 1, 2, 2.
6. Стороны основания прямоугольного параллелепипеда равны 9м. и 12м., а диагональ наклонена к плоскости основания под углом 450. Найдите высоту параллелепипеда.
7. Высота прямой призмы равна 10см. Основанием призмы является прямоугольник со сторонами 6см. и 8см. Найдите площадь диагонального сечения.
8. В правильной четырёхугольной призме диагональ боковой грани 23м., а диагональ основания 20м. Найдите диагональ призмы.
9.Длины рёбер прямоугольного параллелепипеда равны 6см.. 8см. и 24см. Найдите длины его диагоналей.
10. В основании прямой призмы лежит прямоугольник со сторонами 2м. и 2 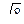 м. Диагональ призмы наклонена к плоскости основания под углом 450. Найдите длину бокового ребра.
11. В прямой призме основанием является прямоугольник со сторонами 2м. и 4м. Высота этой призме равна 3м. Найдите площадь диагонального сечения.
12.АВСА1В1С1- прямая треугольная призма, в основании которой лежит равнобедренный треугольник со сторонами 10см., 10см. и 13см. Найдите площадь сечения, проходящего через вершину В и ребро А1С1, если высота призмы равна 2см. м. Диагональ призмы наклонена к плоскости основания под углом 450. Найдите длину бокового ребра.
11. В прямой призме основанием является прямоугольник со сторонами 2м. и 4м. Высота этой призме равна 3м. Найдите площадь диагонального сечения.
12.АВСА1В1С1- прямая треугольная призма, в основании которой лежит равнобедренный треугольник со сторонами 10см., 10см. и 13см. Найдите площадь сечения, проходящего через вершину В и ребро А1С1, если высота призмы равна 2см.
|
13. В правильной четырёхугольной призме диагональ боковой грани 10м., а диагональ основания 8 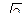 м. Найдите площадь диагонального сечения.
14 Найдите диагональ прямоугольного параллелепипеда, если диагонали его граней имеют длины 11, 19 и 20м.
15. В прямоугольном параллелепипеде стороны основания равны 5см. и 12см., а диагональ параллелепипеда наклонена к плоскости основания под углом 450. Найдите высоту параллелепипеда.
16. Основанием прямой призмы служит прямоугольник. Диагональ основания равна 6дм., а диагональ призмы 8дм. Найдите площадь диагонального сечения.
17. Сторона основания правильной треугольной призмы равна 24м, а высота призмы 18см. Найдите периметр сечения, проведённого через сторону нижнего основания и противолежащую вершину верхнего основания.
18. Определите диагонали прямоугольного параллелепипеда по трём его измерениям 2, 3, 6.
19. Стороны прямоугольника, который лежит в основании прямой призмы, равны 4см и 6см. Высота-8см. Найдите площадь диагонального сечения.
20. Найдите высоту правильной четырёхугольной призмы, если сторона основания равна 2м, а диагональ составляет с плоскостью основания угол 450.
21. В правильной треугольной призме сторона основания равна 12м., а высота – 9м. Найдите периметр сечения, проходящего через вершину С и ребро А1В1.
22. Сторона основания правильной четырёхугольной призмы равна 4м, а высота- 8м. Найдите площади боковых поверхностей треугольной призмы, образованной диагональным сечением.
23. В основании прямоугольного параллелепипеда лежит квадрат со стороной 4см. Диагональ параллелепипеда образует с плоскостью основания угол 600. Найдите высоту призмы.
24. В правильной треугольной призме сторона основания равна 8см., а высота 6см. Найдите площадь сечения, проведенного через ребро А1С1 и вершину В. м. Найдите площадь диагонального сечения.
14 Найдите диагональ прямоугольного параллелепипеда, если диагонали его граней имеют длины 11, 19 и 20м.
15. В прямоугольном параллелепипеде стороны основания равны 5см. и 12см., а диагональ параллелепипеда наклонена к плоскости основания под углом 450. Найдите высоту параллелепипеда.
16. Основанием прямой призмы служит прямоугольник. Диагональ основания равна 6дм., а диагональ призмы 8дм. Найдите площадь диагонального сечения.
17. Сторона основания правильной треугольной призмы равна 24м, а высота призмы 18см. Найдите периметр сечения, проведённого через сторону нижнего основания и противолежащую вершину верхнего основания.
18. Определите диагонали прямоугольного параллелепипеда по трём его измерениям 2, 3, 6.
19. Стороны прямоугольника, который лежит в основании прямой призмы, равны 4см и 6см. Высота-8см. Найдите площадь диагонального сечения.
20. Найдите высоту правильной четырёхугольной призмы, если сторона основания равна 2м, а диагональ составляет с плоскостью основания угол 450.
21. В правильной треугольной призме сторона основания равна 12м., а высота – 9м. Найдите периметр сечения, проходящего через вершину С и ребро А1В1.
22. Сторона основания правильной четырёхугольной призмы равна 4м, а высота- 8м. Найдите площади боковых поверхностей треугольной призмы, образованной диагональным сечением.
23. В основании прямоугольного параллелепипеда лежит квадрат со стороной 4см. Диагональ параллелепипеда образует с плоскостью основания угол 600. Найдите высоту призмы.
24. В правильной треугольной призме сторона основания равна 8см., а высота 6см. Найдите площадь сечения, проведенного через ребро А1С1 и вершину В.
|
 25. Площадь основания правильной четырёхугольной призмы равна 81дм2, а высота-5дм. Найдите площади боковых поверхностей треугольных призм, образованных диагональным сечением.
26. В правильной четырёхугольной призме расстояние от вершины верхнего основания до середины диагонали нижнего основания равно 10см. Высота призмы 6см. Найдите длины сторон оснований призмы.
27. В правильной четырёхугольной призме ABCDA1B1C1D1 площадь основания равна 16см2. Найдите расстояние между прямыми АА1 и В1D.
28.В правильной треугольной призме боковое ребро равно 3см., а расстояние от вершины верхнего основания до середины противоположной стороны нижнего основания равно 6см. Найдите длины остальных рёбер призмы. 25. Площадь основания правильной четырёхугольной призмы равна 81дм2, а высота-5дм. Найдите площади боковых поверхностей треугольных призм, образованных диагональным сечением.
26. В правильной четырёхугольной призме расстояние от вершины верхнего основания до середины диагонали нижнего основания равно 10см. Высота призмы 6см. Найдите длины сторон оснований призмы.
27. В правильной четырёхугольной призме ABCDA1B1C1D1 площадь основания равна 16см2. Найдите расстояние между прямыми АА1 и В1D.
28.В правильной треугольной призме боковое ребро равно 3см., а расстояние от вершины верхнего основания до середины противоположной стороны нижнего основания равно 6см. Найдите длины остальных рёбер призмы.
|
| ЗАДАЧИ (пирамида) |
1. В правильной треугольной пирамиде сторона основания равна 12 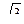 см., а каждое боковое ребро 13см. Найдите высоту пирамиды.
2. В основании пирамиды лежит прямоугольник со сторонами 3м. и 3 см., а каждое боковое ребро 13см. Найдите высоту пирамиды.
2. В основании пирамиды лежит прямоугольник со сторонами 3м. и 3 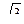 м. Высота пирамиды равна 4м. Найдите длину бокового ребра.
3. Найдите сторону основания правильной треугольной пирамиды, если высота пирамиды равна 6м., а апофема 10м.
4. В правильной четырёхугольной пирамиде сторона основания равна 12мм., а апофема 8мм. Найдите боковое ребро пирамиды.
5. В основании пирамиды лежит прямоугольник, гипотенуза которого равна 13м., а один из катетов-12м. Найдите площадь сечения, проведённого через середину высоты пирамиды, параллельно её основанию.
6. Каждая боковая грань правильной треугольной пирамиды наклонена к плоскости основания под углом 300. Найдите сторону основания, если высота пирамиды равна 10мм.
7. Найдите сторону основания правильной треугольной пирамиды, если известно, что высота пирамиды равна 21м., а длина бокового ребра-29м. м. Высота пирамиды равна 4м. Найдите длину бокового ребра.
3. Найдите сторону основания правильной треугольной пирамиды, если высота пирамиды равна 6м., а апофема 10м.
4. В правильной четырёхугольной пирамиде сторона основания равна 12мм., а апофема 8мм. Найдите боковое ребро пирамиды.
5. В основании пирамиды лежит прямоугольник, гипотенуза которого равна 13м., а один из катетов-12м. Найдите площадь сечения, проведённого через середину высоты пирамиды, параллельно её основанию.
6. Каждая боковая грань правильной треугольной пирамиды наклонена к плоскости основания под углом 300. Найдите сторону основания, если высота пирамиды равна 10мм.
7. Найдите сторону основания правильной треугольной пирамиды, если известно, что высота пирамиды равна 21м., а длина бокового ребра-29м.
|
8. Дана четырёхугольная пирамида в основании которой лежит прямоугольник со сторонами 6дм. и 2 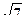 дм. Каждое боковое ребро наклонено к плоскости основания под углом 600. Найдите длину бокового ребра.
9. Найдите апофему правильной треугольной пирамиды, если сторона основания равна 4 дм. Каждое боковое ребро наклонено к плоскости основания под углом 600. Найдите длину бокового ребра.
9. Найдите апофему правильной треугольной пирамиды, если сторона основания равна 4 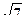 см., а длина каждого бокового ребра 6см.
10. Стороны оснований правильной усечённой треугольной пирамиды 4дм. и 1дм. Боковое ребро 2дм. Найдите высоту пирамиды.
11. Апофема правильной треугольной пирамиды равна 6дм., а сторона основания 6 см., а длина каждого бокового ребра 6см.
10. Стороны оснований правильной усечённой треугольной пирамиды 4дм. и 1дм. Боковое ребро 2дм. Найдите высоту пирамиды.
11. Апофема правильной треугольной пирамиды равна 6дм., а сторона основания 6 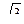 дм. Найдите высоту пирамиды.
12. Сторона основания правильной четырёхугольной пирамиды равна 4 дм. Найдите высоту пирамиды.
12. Сторона основания правильной четырёхугольной пирамиды равна 4 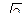 м. Найдите апофему данной пирамиды, если длина бокового ребра равна 5м.
13. Основание пирамиды- прямоугольник со сторонами 6см. и 8см. Каждое боковое ребро пирамиды равно 10см. Найдите высоту пирамиды.
14. В правильной треугольной пирамиде боковые ребра наклонены к плоскости основания под углом 300. Сторона основания равна 12м. Найдите высоту пирамиды.
15. Высота правильной треугольной пирамиды равна 12см., а апофема 13см. Найдите длину бокового ребра пирамиды.
16. Высота правильной четырёхугольной усечённой пирамиды равна 4дм. Стороны оснований-2дм. и 8дм. Найдите площади диагональных сечений.
17. Найдите сторону основания правильной четырёхугольной пирамиды, если высота пирамиды равна 2 м. Найдите апофему данной пирамиды, если длина бокового ребра равна 5м.
13. Основание пирамиды- прямоугольник со сторонами 6см. и 8см. Каждое боковое ребро пирамиды равно 10см. Найдите высоту пирамиды.
14. В правильной треугольной пирамиде боковые ребра наклонены к плоскости основания под углом 300. Сторона основания равна 12м. Найдите высоту пирамиды.
15. Высота правильной треугольной пирамиды равна 12см., а апофема 13см. Найдите длину бокового ребра пирамиды.
16. Высота правильной четырёхугольной усечённой пирамиды равна 4дм. Стороны оснований-2дм. и 8дм. Найдите площади диагональных сечений.
17. Найдите сторону основания правильной четырёхугольной пирамиды, если высота пирамиды равна 2 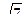 м., а апофема 8м.
18. Боковое ребро пирамиды разделено на четыре равные части и через точки деления проведены плоскости, параллельные основанию. Площадь основания равна 400см2. Найдите площади сечений.
19. Основание пирамиды – прямоугольник со сторонами 8см. и 6см. Высота пирамиды равна 12см. Найдите длину бокового ребра. м., а апофема 8м.
18. Боковое ребро пирамиды разделено на четыре равные части и через точки деления проведены плоскости, параллельные основанию. Площадь основания равна 400см2. Найдите площади сечений.
19. Основание пирамиды – прямоугольник со сторонами 8см. и 6см. Высота пирамиды равна 12см. Найдите длину бокового ребра.
|
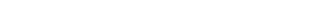 20. В правильной треугольной пирамиде сторона основания равна 3 20. В правильной треугольной пирамиде сторона основания равна 3 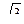 м. Высота пирамиды равна 4м. Найдите длину бокового ребра.
21. В основании пирамиды лежит прямоугольный треугольник, гипотенуза которого равна 25м., а катет 7м. Найдите площадь сечения, проведенного через середину высоты пирамиды параллельно её основанию.
22. Найдите сторону основания правильной четырёхугольной пирамиды, если боковое ребро равно 6м., а высота 2м.
23. Найдите длину бокового ребра правильной треугольной пирамиды, если апофема пирамиды равна 41мм., а высота 40мм.
24. Найдите высоту правильной четырёхугольной пирамиды, если сторона основания равна 7 м. Высота пирамиды равна 4м. Найдите длину бокового ребра.
21. В основании пирамиды лежит прямоугольный треугольник, гипотенуза которого равна 25м., а катет 7м. Найдите площадь сечения, проведенного через середину высоты пирамиды параллельно её основанию.
22. Найдите сторону основания правильной четырёхугольной пирамиды, если боковое ребро равно 6м., а высота 2м.
23. Найдите длину бокового ребра правильной треугольной пирамиды, если апофема пирамиды равна 41мм., а высота 40мм.
24. Найдите высоту правильной четырёхугольной пирамиды, если сторона основания равна 7 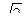 м., а каждое боковое ребро наклонено к плоскости основания под углом 450.
25. Дана пирамида KLMNF, основание LMNF- прямоугольник со сторонами 2 м., а каждое боковое ребро наклонено к плоскости основания под углом 450.
25. Дана пирамида KLMNF, основание LMNF- прямоугольник со сторонами 2 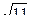 м. и 10м. Каждое боковое ребро пирамиды равно 10м. Найдите высоту пирамиды.
26. Все боковые грани треугольной пирамиды составляют с плоскостью основания угол 450. Найдите высоту пирамиды, если стороны основания равны 20, 21 и 29см.
27. В основании пирамиды лежит равнобедренная трапеция, основания которой равны 16 и 4см. Найдите высоту пирамиды, если каждая её боковая грань составляет с плоскостью основания угол 600.
28. Основанием пирамиды является равнобедренный треугольник с углом 1200. Боковые рёбра образуют с её высотой, равной 16см., углы в 450. Найдите площадь основания пирамиды. м. и 10м. Каждое боковое ребро пирамиды равно 10м. Найдите высоту пирамиды.
26. Все боковые грани треугольной пирамиды составляют с плоскостью основания угол 450. Найдите высоту пирамиды, если стороны основания равны 20, 21 и 29см.
27. В основании пирамиды лежит равнобедренная трапеция, основания которой равны 16 и 4см. Найдите высоту пирамиды, если каждая её боковая грань составляет с плоскостью основания угол 600.
28. Основанием пирамиды является равнобедренный треугольник с углом 1200. Боковые рёбра образуют с её высотой, равной 16см., углы в 450. Найдите площадь основания пирамиды.
|
| 3.3 ДОПОЛНИТЕЛЬНЫЕ ЗАДАНИЯ |
| 1. На поверхности геометрических тел нарисованы различные узоры. Изобразите развёртки поверхностей этих тел и покажите на них соответствующие узоры. |
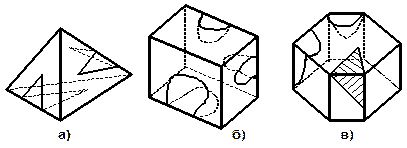 2. Постройте развёртку поверхности:
1) прямоугольного параллелепипеда с рёбрами 5см, 2см, 3см.;
2) прямого параллелепипеда, если его высота равна 6см и основанием является: а) параллелограмм, один из углов которого равен 500 и стороны –
а) 4,6см и 2см.;
б) ромб с углом 600 и меньшей диагональю 4см.
3)прямой призмы, если её высота равна 5см и в основании лежит:
а) трапеция АВСD, причём AD||ВС, ÐА=600, АВ=ВС= 2см, AD=5см;
б) равнобедренный треугольник, с основанием 4см и боковой стороной 2,5см.
4) правильной призмы, если её высота равна 6см и в основании лежит:
а) пятиугольник, вписанный в окружность радиуса 3см;
б) шестиугольник со стороной 3см.
Склейте из всех этих развёрток модели различных призм.
3. Постарайтесь как можно быстрее определить, сколько в каждом сооружении не хватает кубиков до полного куба.
2. Постройте развёртку поверхности:
1) прямоугольного параллелепипеда с рёбрами 5см, 2см, 3см.;
2) прямого параллелепипеда, если его высота равна 6см и основанием является: а) параллелограмм, один из углов которого равен 500 и стороны –
а) 4,6см и 2см.;
б) ромб с углом 600 и меньшей диагональю 4см.
3)прямой призмы, если её высота равна 5см и в основании лежит:
а) трапеция АВСD, причём AD||ВС, ÐА=600, АВ=ВС= 2см, AD=5см;
б) равнобедренный треугольник, с основанием 4см и боковой стороной 2,5см.
4) правильной призмы, если её высота равна 6см и в основании лежит:
а) пятиугольник, вписанный в окружность радиуса 3см;
б) шестиугольник со стороной 3см.
Склейте из всех этих развёрток модели различных призм.
3. Постарайтесь как можно быстрее определить, сколько в каждом сооружении не хватает кубиков до полного куба.
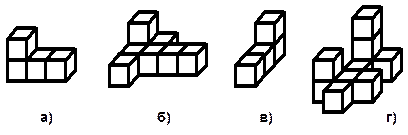
|
| 4. Какие предметы или фигуры можно получить, если сложить несколько: а) пирамид одинаковой величины; б) призм одинаковой величины. По возможности сделайте рисунок. 5. От деревянных моделей пирамид и призмы отпилили по кусочку разной формы, а оставшиеся части изобразили на рисунке. Нарисуйте отпиленные кусочки.
6. Постройте развёртку поверхности правильной пирамиды, боковое ребро которой равно 5,5см, а основание является: а) равносторонним треугольником со стороной 4,3см; б) квадратом с диагональю 5см; в) ромбом со стороной 4см и одним из углов, равным 850; г) правильный шестиугольник со стороной 3см. Склейте из всех этих развёрток модели пирамид.
7. Вам предлагается 12 равносторонних треугольников и 6 прямоугольников. Развёртки каких многогранников можно получить в результате соединения в разном порядке данных фигур.
8. На какие многогранники разбивает призму АВСА1В1С1 плоскость, проходящая через вершины А, В и С1? Какие особенности имеют эти многогранники? Сделайте рисунок. 9. В кубе АВСDА 1В 1С 1D1 из вершины D1 проведены диагонали граней D1A, D1B1, D1C. Как называется многогранник с вершинами D1, А, В1, С? Имеет ли этот многогранник равные рёбра? равные грани? 10. Вершинами некоторого многогранника являются центр верхней грани куба и середины всех сторон нижней его грани. Как называется этот многогранник? Сделайте рисунок и обозначьте равные рёбра многогранника; укажите, какие грани этого многогранника равны между собой. 11. Дана треугольная пирамида SАВС, АВС – основание. Точки М и N принадлежат основанию пирамиды, но не лежат на рёбрах АВ, ВС, АС. Покажите на рисунке сечение этой пирамиды плоскостью, проходящей через точки S, М и N. | |||||
| 12. В этих рисунках допущены ошибки. Найдите и исправьте их.
13. Дана прямая треугольная призма АВСА1В1С1: точка К – середина ребра А1В1, точки М и N – внутренние точки отрезков АВ и ВС, не совпадающие с их серединами. Покажите на рисунке сечение этой призмы плоскостью, проходящей через точки К, М, N. 14. В каждой строке написано пять слов, из которых четыре можно объединить в одну группу и дать ей название, а одно слово к этой группе не относится. Найдите это слово и назовите оставшуюся группу. 1) Призма, куб, пирамида, параллелепипед, прямоугольный параллелепипед. 2) Вершина, куб, ребро, основание, высота. 3) Призма, куб, октаэдр, тетраэдр, додекаэдр. 4) Ромб, треугольник, прямоугольник, пирамида, трапеция.
| |||||
| 15. Постарайтесь как можно быстрее определить, сколько многогранников изображено на рисунке? Назовите их.
| |||||
|
ТЕЛА ВРАЩЕНИЯ | |||||
|
ЦИЛИНДР | |||||
|
Прямым круговым цилиндром называется фигура, полученная при вращении прямоугольника вокруг оси, содержащей одну из его сторон.
|
Элементы цилиндра: R - радиус основания; D - диаметр основания; ОО1- ось вращения цилиндра; Н- высота; L – образующая. | ||||
|
ABCD- осевое сечение |
Круг k – поперечное сечение |
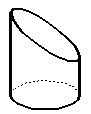
Усеченный цилиндр | |||
|
КОНУС | |||||
|
Прямым круговым конусом называется фигура, полученная при вращении прямоугольного треугольника вокруг оси, содержащий его катет. |
Элементы конуса: R – радиус основания; D – диаметр основания; Н – высота; L – образующая.
| ||||
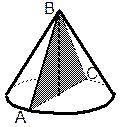 АВС – осевое сечение (равнобедренный треугольник)
АВС – осевое сечение (равнобедренный треугольник)
|
Круг k – поперечное сечение |
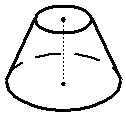 Усеченный конус
Усеченный конус
| |||
| ШАР |
СФЕРА | |
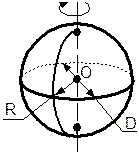 Шар – тело, получаемое вращением полукруга того же радиуса вокруг прямой, содержащий диаметр, ограничивающий этот полукруг.
R – радиус полукруга (равен радиусу шара).
D – диаметр шара.
О – центр шара.
Шар – тело, получаемое вращением полукруга того же радиуса вокруг прямой, содержащий диаметр, ограничивающий этот полукруг.
R – радиус полукруга (равен радиусу шара).
D – диаметр шара.
О – центр шара.
|
Сфера (шаровая поверхность) – замкнутая поверхность, получаемая вращением полуокружности вокруг прямой, содержащей стягивающий ее диаметр.
R – радиус сферы. О – центр сферы. | |
Дата: 2018-12-21, просмотров: 8973. | ||