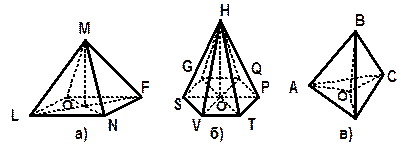
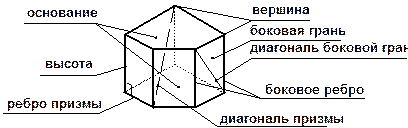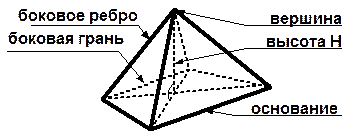| Дано: АВСD прямоугольник; КÏ АВСD; АК^ АВСD; КВ=7м; КС=9м; КD=6м. Найти: АК. |
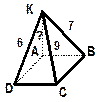
| Решение: 1) Рассмотрим D он прямоугольный (АК^ АВСD), по теореме Пифагора КD2= АК2+АD2 ÞАК2=КD2-АD2, КD=6м, АD-? 2) Найдём АD. Для этого рассмотрим DКВС. Здесь КВ- наклонная, АВ- её проекция, АВ^ВС(т. к. АВСD- | ||
| прямоугольник), значит по ТТП (теорема трёх перпендикуляров) КВ^ВСÞDКВС прямоугольный (ÐКВС=900), тогда по теореме Пифагора ВС2=КС2-КВ2, причём ВС=АD т. к. АВСD – прямоугольник, тогда АD2=КС2-КВ2. 3) Найдём АК. АК2=КD2-АD2= КD2-(КC2-КВ2)=62-(92-72)=36 – (81-49)=4, АК= 3. Точка L находится на расстоянии 10см. от вершин равностороннего треугольника АВС со стороной АВ=8 | ||||
| Дано: DАВС- равносторонний; LÏDАВС; LA=10см; АВ=8 Найти: а) L О б) S D АО L ; в) L К. | 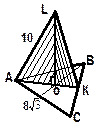
| Решение: 1) Опустим перпендикуляр из точки L на плоскость АВС, обозначим точку пересечения перпендикуляра и плоскости точкой О, значит LО- расстояние от точки О до плоскости DАВС. Рассмотрим DАОL прямоугольный Þ по теореме Пифагора | ||
| АL2=АО2+LО2, тогда LО2=АL2-АО2. 2) АО-? АО=R (радиус описанной окружности около DАВС), R= | ||||
| LО= 3) SDАОL= 4) Опустим перпендикуляр LK на сторону ВС (LK- расстояние от точки L до стороны ВС). Рассмотрим DLОК , он прямоугольный, т. к. LО^АВС, тогда по теореме Пифагора LK2=LO2+ОК2, LO=6см., КО-?. 5) Найдём КО, для этого рассмотрим DАВС, здесь КО=r (радиус вписанной окружности в треугольник), r = LK2=62 + 42 =52, LK= Ответ: LO=6см, SDАОL=24см2, LK=2
4. Из точек А и В, лежащих в двух перпендикулярных плоскостях, опущены перпендикуляры АС и В D на прямую пересечения плоскостей. Найдите длину отрезка АВ, если АС= 6м, В D = 7м, CD =6м. | ||||
Дано:
a^b; АÎa, ВÎb;
a  b=c;
АС^c, BD^c;
АС=6м, BD=7м;
CD=6м.
Найти: АВ. b=c;
АС^c, BD^c;
АС=6м, BD=7м;
CD=6м.
Найти: АВ.
|
| Решение: 1) Рассмотрим DАВС- он прямоугольный, т. к. АС^CD и a^b, значит АС^СВ ( по свойству перпендикулярных плоскостей). Тогда по теореме Пифагора АВ2= АС2+СВ2, АС=6м, СВ-? 2) Найдём СВ. Для этого | ||
| рассмотрим DCDB (BD^CD по условию), по теореме Пифагора СВ2=CD2+BD2. 3) Значит АВ2 =АС2+(CD2+BD2) = 62+72+62 = 121, АВ= Ответ: АВ=11м. | ||||
| Рисунки к задачам |
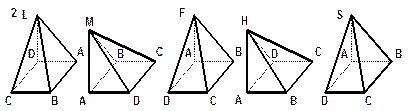
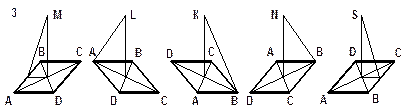
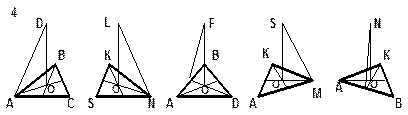
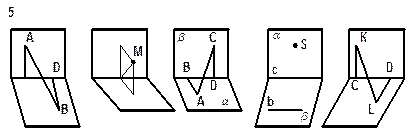
|
| 2.8 ЗАДАЧИ |
1. Из центра О квадрата АВСD со стороной 18 м. к его плоскости проведён перпендикуляр ОМ длиной 12 м. Найдите: а) расстояние от точки М до стороны АВ; б) площадь треугольника АМВ.
2. Даны прямоугольник АВСD и точка F вне его плоскости. Прямая АF перпендикулярна прямым АВ и АD.Известно, что стороны прямоугольника
АВ = 4 см., АD = 3 см., а длина перпендикуляра АF = 12 см. Найдите: а) длину отрезка FС; б) SDFАС.
3. Прямые АВ и СD перпендикулярны некоторой плоскости и пересекают её в точках В и D соответственно. Найдите АС, если АВ = 9дм., СD = 15дм., ВD = 8дм. и точки А и С лежат по одну сторону плоскости.
4. Из центра О правильного треугольника АВС со стороной 3 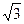 м. проведён перпендикуляр ОD к его плоскости длиной 4м. Найдите расстояние от точки D до вершины треугольника.
5. Из точек А и В, лежащих в двух перпендикулярных плоскостях, опущены перпендикуляры АС и ВD на прямую пересечения плоскостей. Найдите длину отрезка АВ, если АС = 3 м., ВD = 4 м., СD = 12 м..
6. Через концы отрезка МН проведены прямые, перпендикулярные некоторой плоскости и пересекающие её в точках К и Т соответственно. Найдите МН, если КТ = 5 дм, МК =6 дм., НТ = 4 дм. и точки М и Н находятся по одну сторону от плоскости.
7. Дан прямоугольник АВСD и точка L вне его плоскости. Прямая LD перпендикулярна прямым AB и AD. Длина отрезка LD=6см., а стороны прямоугольника- AB=4см, AD=3см. Найдите: а) длину отрезка LB; б) SDLBC.
8. Плоскости a и b перпендикулярны. В плоскости a взята точка S, расстояние от которой до прямой с (линии пересечения плоскостей) равно 0,5 м. В плоскости b проведена прямая b, параллельная прямой с и отстоящая на 1,2 м от нее. Найдите расстояние от точки S до прямой b.
9. Точка L находится на расстоянии 10см от вершины прямоугольника ABCD со сторонами 6 см и 8 см. Найдите:
а) расстояние от точки L до плоскости прямоугольника LO; м. проведён перпендикуляр ОD к его плоскости длиной 4м. Найдите расстояние от точки D до вершины треугольника.
5. Из точек А и В, лежащих в двух перпендикулярных плоскостях, опущены перпендикуляры АС и ВD на прямую пересечения плоскостей. Найдите длину отрезка АВ, если АС = 3 м., ВD = 4 м., СD = 12 м..
6. Через концы отрезка МН проведены прямые, перпендикулярные некоторой плоскости и пересекающие её в точках К и Т соответственно. Найдите МН, если КТ = 5 дм, МК =6 дм., НТ = 4 дм. и точки М и Н находятся по одну сторону от плоскости.
7. Дан прямоугольник АВСD и точка L вне его плоскости. Прямая LD перпендикулярна прямым AB и AD. Длина отрезка LD=6см., а стороны прямоугольника- AB=4см, AD=3см. Найдите: а) длину отрезка LB; б) SDLBC.
8. Плоскости a и b перпендикулярны. В плоскости a взята точка S, расстояние от которой до прямой с (линии пересечения плоскостей) равно 0,5 м. В плоскости b проведена прямая b, параллельная прямой с и отстоящая на 1,2 м от нее. Найдите расстояние от точки S до прямой b.
9. Точка L находится на расстоянии 10см от вершины прямоугольника ABCD со сторонами 6 см и 8 см. Найдите:
а) расстояние от точки L до плоскости прямоугольника LO;
|
б) площадь треугольника ALC.
10. Точка S не принадлежит плоскости равностороннего треугольника. Найдите сторону треугольника, если расстояние от точки S до вершин треугольника 13дм., а до плоскости треугольника – 5дм.
11. Расстояние от точки S до сторон квадрата ABCD равно 10 дм, а до плоскости квадрата 6дм. Найдите: а) сторону квадрата; б) площадь треугольника ASD.
12. Точка М находится на расстоянии 12 см и 5 см от двух перпендикулярных плоскостей. Найдите расстояние от этой точки до линии пересечения плоскостей.
13. Отрезок MH не имеет общих точек с плоскостью. Прямые МР и НО, перпендикулярные этой плоскости, пересекают её в точках Р и О соответственно. МР=12мм., МН=13мм., НО=24мм. Найдите РО.
14. Точка L находится на расстоянии 10м. от вершины равностороннего треугольника со стороной 8 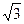 м. Найдите расстояние от точки L до плоскости треугольника.
15. Точка М не принадлежит плоскости квадрата ABCD. Прямая АМ перпендикулярна прямой АВ и АD, причем АВ=8 м, АМ=6 м. Найдите:
а) длину отрезка МС; б) площадь треугольника MDB.
16. Прямая SA перпендикулярна плоскости прямоугольника ABCD. Стороны АВ и АС прямоугольника равны 7 см и 5 см. соответственно, а отрезок SC=13 см. Найдите: а) длину отрезка SB;
б) площадь треугольника SDC.
17. Дан квадрат ABCD со стороной 8 м. Найдите расстояние от точки L до плоскости треугольника.
15. Точка М не принадлежит плоскости квадрата ABCD. Прямая АМ перпендикулярна прямой АВ и АD, причем АВ=8 м, АМ=6 м. Найдите:
а) длину отрезка МС; б) площадь треугольника MDB.
16. Прямая SA перпендикулярна плоскости прямоугольника ABCD. Стороны АВ и АС прямоугольника равны 7 см и 5 см. соответственно, а отрезок SC=13 см. Найдите: а) длину отрезка SB;
б) площадь треугольника SDC.
17. Дан квадрат ABCD со стороной 8 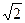 м. Из точки N в центр квадрата опущен перпендикуляр. Угол между отрезком NA и плоскостью квадрата равен 600. Найдите: а) расстояние от точки N до вершин квадрата; б) площадь треугольника ANC.
18. Из точек К и L, лежащих в двух перпендикулярных плоскостях, опущены перпендикуляры KC и LD на прямую пересечения плоскостей. Найдите длину отрезка KL, если KD=LC=5м, CD=1м.
19. Сторона равностороннего треугольника равна 12 м. Из точки N в центр квадрата опущен перпендикуляр. Угол между отрезком NA и плоскостью квадрата равен 600. Найдите: а) расстояние от точки N до вершин квадрата; б) площадь треугольника ANC.
18. Из точек К и L, лежащих в двух перпендикулярных плоскостях, опущены перпендикуляры KC и LD на прямую пересечения плоскостей. Найдите длину отрезка KL, если KD=LC=5м, CD=1м.
19. Сторона равностороннего треугольника равна 12 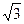 дм. Найдите расстояние до сторон треугольника от точки, которая находится на расстоянии 8 дм от плоскости треугольника. дм. Найдите расстояние до сторон треугольника от точки, которая находится на расстоянии 8 дм от плоскости треугольника.
|
20. Через точки А и В проведены прямые, перпендикулярные плоскости a, пересекающие её в точках С и D соответственно. Найдите расстояние между точками B и D, если АС=3 м, АВ=2,6 м, CD=2,4 м и отрезок АВ не пересекает плоскость a.
21. Из центра О квадрата ABCD восстановлен перпендикуляр ОК длиной 9 м. Расстояние от точки К до вершин квадрата равно 15 м. Найдите: а) сторону квадрата; б) SDАКС.
22. Стороны равностороннего треугольника равны 5 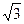 см. Найдите расстояние до плоскости треугольника от точки, которая находится на расстоянии 8см от каждой стороны.
23.Дан квадрат АВСD и точка Н вне его плоскости, причем АН ^ ABCD. Длина отрезка НС=10 дм, а сторона квадрата 5 дм. Найдите: а) длину отрезка НВ; б) SDHАС.
24. Из точек А и В, лежащих в перпендикулярных плоскостях a и b, опущены перпендикуляры АС и BD на прямую пересечения плоскостей. Найдите длину отрезка АВ, если: AD= 4 м, ВС=3 м, CD=2 м.
25. Телефонная проволока длиной 15 м протянута от телефонного столба, где она прикреплена на высоте 8 м от поверхности земли, к дому. Найдите, на какой высоте прикрепили к дому проволоку, если расстояние между домом и столбом равно 9 м.
26. Из точки к плоскости проведены две наклонные. Найдите длины наклонных, если одна из них на 26 см больше другой, а проекции наклонных равны 12 см и 40 см.
27. Отрезок МН пересекает некоторую плоскость в точке К. Через концы отрезка проведены прямые НР и МЕ, перпендикулярные плоскости и пересекающие её в точках Р и Е. Найти РЕ, если НР=4дм., НК=5дм., МЕ=12дм..
28. Прямые АВ и CD перпендикулярны некоторой плоскости и пересекают её в точках В и D соответственно. Найти АС, если АВ=9м., СD=15м., ВD=8м. и точки А и С лежат по разные стороны плоскости.
29. Из точки к плоскости проведены две наклонные, равные 23 см и 33 см. Найдите расстояние от этой точки до плоскости, если проекции наклонных относятся как 2:3. см. Найдите расстояние до плоскости треугольника от точки, которая находится на расстоянии 8см от каждой стороны.
23.Дан квадрат АВСD и точка Н вне его плоскости, причем АН ^ ABCD. Длина отрезка НС=10 дм, а сторона квадрата 5 дм. Найдите: а) длину отрезка НВ; б) SDHАС.
24. Из точек А и В, лежащих в перпендикулярных плоскостях a и b, опущены перпендикуляры АС и BD на прямую пересечения плоскостей. Найдите длину отрезка АВ, если: AD= 4 м, ВС=3 м, CD=2 м.
25. Телефонная проволока длиной 15 м протянута от телефонного столба, где она прикреплена на высоте 8 м от поверхности земли, к дому. Найдите, на какой высоте прикрепили к дому проволоку, если расстояние между домом и столбом равно 9 м.
26. Из точки к плоскости проведены две наклонные. Найдите длины наклонных, если одна из них на 26 см больше другой, а проекции наклонных равны 12 см и 40 см.
27. Отрезок МН пересекает некоторую плоскость в точке К. Через концы отрезка проведены прямые НР и МЕ, перпендикулярные плоскости и пересекающие её в точках Р и Е. Найти РЕ, если НР=4дм., НК=5дм., МЕ=12дм..
28. Прямые АВ и CD перпендикулярны некоторой плоскости и пересекают её в точках В и D соответственно. Найти АС, если АВ=9м., СD=15м., ВD=8м. и точки А и С лежат по разные стороны плоскости.
29. Из точки к плоскости проведены две наклонные, равные 23 см и 33 см. Найдите расстояние от этой точки до плоскости, если проекции наклонных относятся как 2:3.
|
27. Отрезок МН пересекает некоторую плоскость в точке К. Через концы отрезка проведены прямые НР и МЕ, перпендикулярные плоскости и пересекающие её в точках Р и Е. Найти РЕ, если НР=4дм., НК=5дм., МЕ=12дм..
28. Прямые АВ и CD перпендикулярны некоторой плоскости и пересекают её в точках В и D соответственно. Найти АС, если АВ=9м., СD=15м., ВD=8м. и точки А и С лежат по разные стороны плоскости.
29. Из точки к плоскости проведены две наклонные, равные 23 см и 33см. Найдите расстояние от этой точки до плоскости, если проекции наклонных относятся как 2:3.
30. Точка Е не принадлежит плоскости прямоугольника АВСD, ВЕ 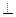 АВ,
АЕ АВ,
АЕ 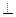 АD. Найти площадь треугольника ЕВD, если ВD=7м., ЕD=25м.
31. В треугольнике АВС АВ=АС=20мм., ВС=24мм. Отрезок АМ перпендикулярен плоскости АВС и равен 12мм. Найти расстояние от точки М до прямой ВС. АD. Найти площадь треугольника ЕВD, если ВD=7м., ЕD=25м.
31. В треугольнике АВС АВ=АС=20мм., ВС=24мм. Отрезок АМ перпендикулярен плоскости АВС и равен 12мм. Найти расстояние от точки М до прямой ВС.
|
|
ДОПОЛНИТЕЛЬНЫЕ ЗАДАНИЯ | |
| 1. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение: а) плоскостью АВС1; б) плоскостью АСС1. Докажите, что построенные сечения являются параллелограммами. 2. Точка S равноудалена от вершин прямоугольного треугольника и не лежит в плоскости этого треугольника. Докажите, что прямая SM где М – середина гипотенузы, перпендикулярна к плоскости треугольника. | |
| 3. Точка М – середина ребра AD куба, изображённого на рисунке. Скопируйте рисунок и изобразите точку N, принадлежащую ребру CD, так, чтобы отрезки А1N и С1М имели общую точку. | 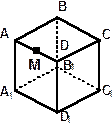
|
| 4. Можно ли из данных плоских фигур получить модели геометрических тел? Если можно, то какие и как это сделать?
| |
| 6. Точки K, L, M и N принадлежат рёбрам изображённой на рисунке пирамиды. Скопируйте рисунок и определите, пересекаются ли прямые KL и MN, отрезки KN и LM. | 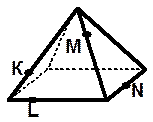
|
| 7. Решите анаграммы и исключите лишнее слово: а) лоннанаяк ; пенлярперкуди; ципрояек; ачток; б) давктар; кинтрельуго; гурк; бук; в) стькоспло; паямяр; ачток; тояраснисе; г) чул; аямпря; козрето; луго.
8. Постройте развёртку поверхности правильной пирамиды, боковое ребро которого равно 5,5см., а основание является: а) равносторонним треугольником со стороной 4,3см; б) квадратом с диагональю 5см; в) ромбом со стороной 4см. и одним из углов, равным 850; г) правильный шестиугольник со стороной 3см. 9. Сколько пирамид изображено на рисунке? Разделение пирамид ведите по линиям.
10. Перерисуйте из приложения (в конце пособия) развёртки треугольной пирамиды и правильной четырёхугольной пирамиды. Склейте из этих развёрток пирамиды и обозначьте разными цветами: а) расстояние от вершины пирамиды до вершин основания; б) расстояние от вершины пирамиды до плоскости основания; в) радиусы вписанной и описанной окружности основания правильной четырёхугольной пирамиды; г) линейный угол между боковой гранью и основанием.
11. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей через диагональ АС основания параллельно диагонали ВD1. Докажите, что если основание параллелепипеда – ромб и углы АВВ1 и СВВ1 прямые, то построенное сечение – равнобедренный треугольник
| |
| 3 МНОГОГРАННИКИ Так называются тела, поверхность которых состоит из конечного числа плоских многоугольников. Многогранник называют выпуклым, если он весь лежит по одну сторону от плоскости любой его грани; тогда грани его тоже выпуклы. |
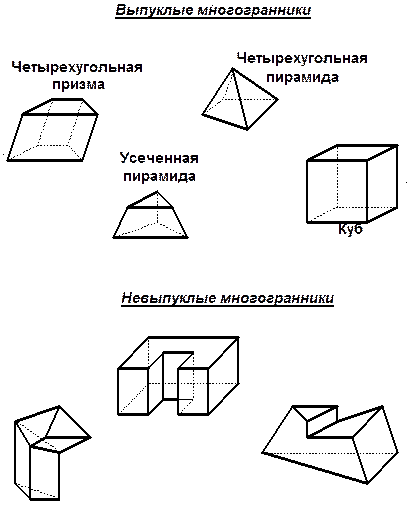
|
|
ПРИЗМА Так называется многогранник, две грани которого (основания) – равные n – угольники, лежащие в параллельных плоскостях, а остальные n- граней (боковые грани) – параллелограммы. | |
|
ОСНОВНЫЕ ЭЛЕМЕНТЫ ПРИЗМЫ | |
|
Высота призмы – перпендикуляр, проведенный из точки одного основания к плоскости другого. Диагональ призмы – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани. Диагональное сечение – сечение, которое проходит через какую-нибудь диагональ призмы и боковое ребро. Поверхность призмы состоит из двух оснований и боковой поверхности. Боковая поверхность состоит из параллелограммов. | |
|
ОСНОВНЫЕ ВИДЫ ПРИЗМ | |
|
| |
| ПАРАЛЛЕЛЕПИПЕД Так называется призма, основания которой параллелограммы. | |
| СВОЙСТВА ПАРАЛЛЕЛЕПИПЕДА Противолежащие грани равны и параллельны. Все четыре диагонали пересекаются в одной точке и точкой пересечения делятся пополам. Точка пересечения диагоналей – центр симметрии. | |
| ВИДЫ ПАРАЛЛЕЛЕПИПЕДОВ | |

| |
|
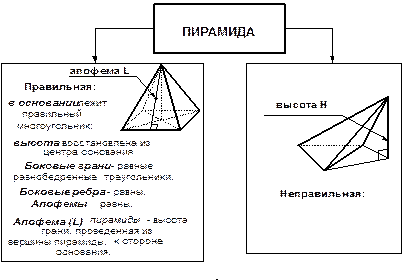
ПИРАМИДА Так называется многогранник, одна грань которого (основание) – многоугольник, а все остальные грани (боковые) - треугольники, имеющие общую вершину (вершина пирамиды). | |
|
ОСНОВНЫЕ ЭЛЕМЕНТЫ ПИРАМИДЫ | |
|
Высота пирамиды – перпендикуляр, опущенный из вершины пирамиды на плоскость основания. Диагональное сечение – сечение, проходящее через два не соседних боковых ребра пирамиды. Поверхность пирамиды состоит из основания и боковых граней. Каждая боковая грань – треугольник. | |
|
ОСНОВНЫЕ ВИДЫ ПИРАМИД | |
|
| |

| |
| ПРАВИЛЬНЫЙ МНОГОГРАННИК Так называется многогранник, у которого: - все грани – равные правильные многоугольники; - все многогранные углы имеют одинаковое число граней; - все ребра – равные отрезки; - все плоские углы – равные углы. | |
| ВИДЫ ПРАВИЛЬНЫХ МНОГОГРАННИКОВ |
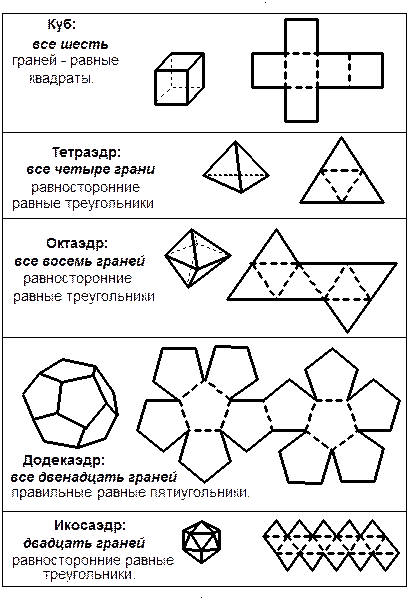
|
|
УПРАЖНЕНИЯ | |
| 1. Какие из фигур, изображенных на рисунке, являются призмами и почему?
2. Существует ли треугольная призма, у которой: а) только две боковые грани - прямоугольники; б) только две боковые грани перпендикулярны плоскости основания; в) только одна боковая грань – прямоугольник? 3. ABCDEFKA 1 B 1 C 1 D 1 E 1 F 1 K 1 - невыпуклая прямая призма. | |
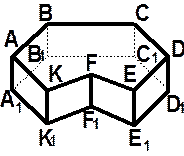
| Выпишите: а) основания; б) параллельные боковые грани; в) все грани, проходящие через точку С; г) все грани параллельные ребру КК1 (см. тему " Параллельные прямая и плоскость"); д) все диагонали призмы. |
| 4. Верно ли утверждение: а) основанием наклонной призмы является правильный многоугольник; б) куб является призмой; в) если призма наклонная, то ее высота равна длине бокового ребра; г) высота призмы – отрезок, соединяющий две вершины, не лежащие в одной грани; д) если сторона основания правильной четырехугольной призмы равна ее высоте, то эта призма куб? 5. Сделайте рисунок наклонной четырехугольной призмы, обозначьте ее и запишите: вершины, основания, боковые ребра, боковые грани, противоположные грани. 6. Среди изображенных тел выберите номера тех, которые являются параллелепипедом.
7. Какое из утверждений является неверным: а) призма – это многогранник; б) параллелепипед – это многоугольник; в) усечённая пирамида - пирамида? 8. Из скольких кубиков с ребром 3 см каждый можно составить куб с ребром 15 см?
| |
| 9. В кубе из одной вершины проведены две диагонали боковых граней. Чему равен угол между ними? | 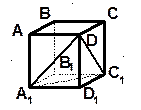
|
| 10. Верно ли утверждение: а) прямоугольник может быть основанием наклонного параллелепипеда; б) наклонный параллелепипед имеет множество плоскостей симметрии; в) параллелепипед имеет четыре диагонали; г) существует такой наклонный параллелепипед, у которого четыре грани прямоугольники?
| |||||||
| 11. Вершинами некоторого многогранника являются центр верхней грани куба, и середины всех сторон нижней его грани. Как называется этот многогранник? Перечислите равные ребра, и укажите какие грани этого многогранника равны между собой. | 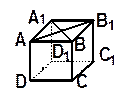
| ||||||
|
12. Ответьте на вопросы а) сколько боковых ребер пирамиды могут быть перпендикулярными к плоскости основания; б) будет ли пирамида правильной, если ее боковыми гранями являются правильные треугольники? 13. Верно ли утверждение: а) пирамида всегда будет правильной, если в ее основании лежит правильный многоугольник; б) высота боковой грани правильной пирамиды – апофема; в) в любой пирамиде можно провести апофему; г) тетраэдр – правильный многогранник; д) наименьшее число ребер, какое может иметь пирамида – шесть; е) тетраэдр имеет несколько плоскостей симметрии, проходящих через данную вершину. 14. В правильной треугольной пирамиде SABC: а) укажите угол между боковой гранью SAB и плоскостью основания АВС, для этого постройте линейный угол этих плоскостей; б) укажите радиус вписанной и описанной окружности основания; | |||||||
| в) вычислите r и R, если АВ=10 см; г) вычислите длину бокового ребра и высоту, если боковое ребро наклонено к плоскости основания под углом 600. 15. Известно, что многогранник, у которого 26 вершин, является призмой. Какой многоугольник лежит в основании этой призмы? Сколько боковых граней имеет эта призма? 16. Может ли пирамида иметь: а) 13 рёбер; б) 14 рёбер; в)13 боковых рёбер? Если такая пирамида существует, то какая она? 17. Может ли призма иметь: а) 15 рёбер; б) 28 рёбер; в) 8 боковых рёбер? Если эта призма существует, то какая она? Сколько у неё боковых рёбер, вершин? | |||||||
|
ПРОЧИТАЙТЕ УСЛОВИЕ ЗАДАЧ И РАЗБЕРИТЕ ИХ РЕШЕНИЕ
Дата: 2018-12-21, просмотров: 6565. | |||||||
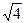 =2(м) . Ответ: АК=4м.
=2(м) . Ответ: АК=4м.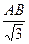 =
= 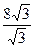 =8(см), АО=8см, значит LО2 = 102 – 82 = 36,
=8(см), АО=8см, значит LО2 = 102 – 82 = 36,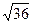 =6(см).
=6(см).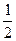 LO*АО=
LO*АО= 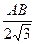 =
= 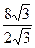 = 4(см)Þ КО=4см. Тогда
= 4(см)Þ КО=4см. Тогда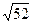 =
= 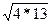 =2
=2 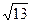 (см).
(см).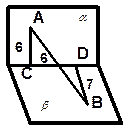
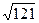 =11(м).
=11(м).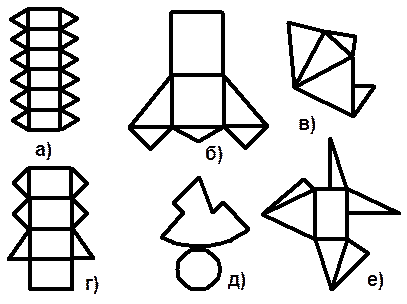 5. Изобразите параллелепипед ABCDA1B1C1D1 и отметьте точки M и N соответственно на рёбрах ВВ1 и СС1. Постройте точку пересечения: а) прямой MN с плоскостью АВС; б) прямой АМ с плоскостью А1В1С1.
5. Изобразите параллелепипед ABCDA1B1C1D1 и отметьте точки M и N соответственно на рёбрах ВВ1 и СС1. Постройте точку пересечения: а) прямой MN с плоскостью АВС; б) прямой АМ с плоскостью А1В1С1.