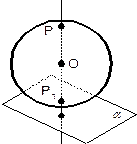
Плоскость a не имеет со сферой общих точек
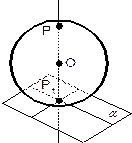 Плоскость a касается сферы в точке Р1 (полюсе)
Плоскость a касается сферы в точке Р1 (полюсе)
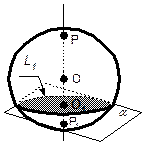
Плоскость  пересекает сферу по окружность L1 с центром О1 на оси.
пересекает сферу по окружность L1 с центром О1 на оси.
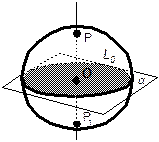 Плоскость
Плоскость 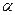 пересекает сферу (проходя через её центр О) по большому кругу L0 с тем же центром.
пересекает сферу (проходя через её центр О) по большому кругу L0 с тем же центром.
УПРАЖНЕНИЯ | ||||
| 1. Ответьте на вопросы. 1. Какие фигуры изображены на рисунке?
2. Имеет ли цилиндр: а) центр симметрии? б) ось симметрии, сколько? в) плоскость симметрии, сколько? 3. Как расположены точки на поверхности цилиндра, равноудаленные от двух точек оснований? 4. Имеет ли конус: а) центр симметрии? б) ось симметрии, сколько? в) плоскость симметрии, сколько? 5. Как расположены точки на поверхности цилиндра, равноудаленные от двух точек образующих? Сделайте рисунок. 6. Имеет ли шар: а) центр симметрии? б) ось симметрии, сколько? в) плоскость симметрии, сколько? 7. Сколько касательных плоскостей к сфере можно провести через точку, взятую: а) на сфере; б) вне сферы. 2. Три шара радиуса R касаются друг друга. Вычислите стороны треугольника, образованного центрами этих шаров.
| ||||
| 3. Нарисуйте тела вращения, образованные вращением плоских фигур вокруг оси m, изображенных на рисунке.
4. Выберите верный ответ. К каждому заданию сделайте рисунок. 1. Радиус основания цилиндра 1.5см, высота – 4см. Чему равна диагональ осевого сечения? а) 4.2см; б) 10см; в) 5см. 2. Осевое сечение цилиндра – квадрат, площадь которого36дм2. Чему равна площадь основания цилиндра? а) 6p дм2; б) 9p дм2; в) 36p дм2. 3. Квадрат со стороной 4см вращается вокруг одной из своих сторон. Чему равна площадь основания полученного тела вращения? а) 2p см2; б) 4pсм2; в) 16p см2. 4. Наибольший угол между образующими конуса 600. Чему равен диаметр основания, если образующая равна 7см? 5. Площадь осевого сечения конуса равна 36см2, а высота 12см. Найдите радиус основания. а) 3см; б) 6см; в) 8см. | ||||
| 5. Точки Аи В расположены на видимой части боковой поверхности цилиндра. Скопируйте рисунок и проведите отрезок АВ. Все ли точки отрезка АВ принадлежат боковой поверхности цилиндра? | 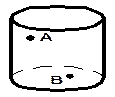
| |||
| 6. Точка А принадлежит основанию конуса, изображённого на рисунке, а точка В – оси SO этого конуса. Скопируйте рисунок и определите, где, внутри или снаружи конуса, расположена точка С прямой АВ. |
| |||
| 7. Точка А принадлежит основанию цилиндра, изображённого на рисунке, а точка В – оси ОО1 этого цилиндра. Скопируйте рисунок и определите, где, внутри или снаружи цилиндра, расположена точка С прямой АВ. |
| |||
|
ПРОЧИТАЙТЕ УСЛОВИЕ ЗАДАЧ И РАЗБЕРИТЕ ИХ РЕШЕНИЕ | ||||
| 1. Осевым сечением цилиндра является квадрат, диагональ которого равна 8 | ||||
Дано:
цилиндр;
АВСD – осев. сеч.;
АВСD – квадрат;
АС= 8 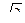 см.
Найти:
Sос. сеч. ; Sосн. см.
Найти:
Sос. сеч. ; Sосн.
|
| Решение:
1) Sос. сеч = SАВСD = АВ2.
Если АВСD – квадрат, то по теореме Пифагора АС = АВ 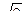 = 8 = 8 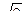 Þ Þ
| ||
| АВ =8(см). Тогда Sос. сеч = 82 = 64(см2). 2) Sосн. = pR2. Так как АВСD – осевое сечение, то R = Ответ: Sос. сеч. = 64см2, Sосн. = 32p. | ||||
| 2. Образующая конуса наклонена к плоскости основания под углом 300. Найдите высоту конуса и площадь осевого сечения, если образующая конуса равна 12мм. | ||
| Дано: конус; АВС – осев. сеч.; L = АВ = 12мм; ÐВАС = 300. Найти: Н, Sос. сеч. . | 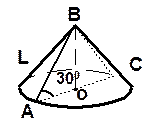
| Решение: 1) Найдём высоту. Для этого рассмотрим D АОВ – он прямоугольный, т. к. ВО – высота. Значит, если АВ = 12(мм), то ВО =12 : 2 = 6(мм). ВО = Н. |
| 2) Sос. сеч. = SDАВС = АС - ? АС = 2АО. Найдём АО из D АОВ по т. Пифагора. АО2 =АВ2 – ВО2 = = 122 – 62 = 108, АО = Тогда Sос. сеч.= Ответ: Н = 6мм, Sос. сеч = 36 3. На расстоянии 8дм от центра шара проведено сечение, площадь которого равна 36дм2. Найдите радиус шара. | ||
Дано:
шар, a 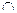 шар ;
Scеч. = 36дм2;
h = ОА = 8дм;
Найти: Rш. шар ;
Scеч. = 36дм2;
h = ОА = 8дм;
Найти: Rш.
|
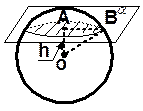
| Решение: 1) Scеч. = pR2 = 36 Þ Rсеч. = 6дм. Rш. - ? Рассмотрим DОАВ, где АВ = Rсеч., ОВ = Rш. и ОА = h, тогда по т. Пифагора |
| ОВ2 = ОА2 + АВ2 = 82 + 62 = 100, ОВ = Ответ: Rш. =10дм. | ||
| РИСУНКИ К ЗАДАЧАМ |
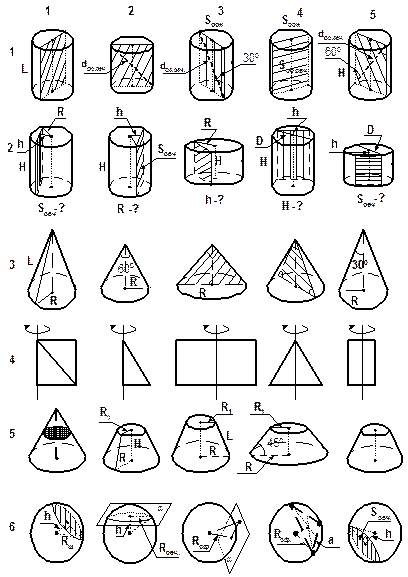
|
| 4.2 ЗАДАЧИ |
| 1. Радиус основания цилиндра равен 5см, а его образующая – 9см. Найдите: площадь основания цилиндра, площадь осевого сечения, диагональ осевого сечения. 2. Высота цилиндра равна 8см, радиус равен 5см. Найдите площадь сечения цилиндра плоскостью, параллельной его оси, если расстояние между этой плоскостью и осью цилиндра равно 3см. |
3. Осевое сечение конуса – равносторонний треугольник со стороной 6дм. Найдите высоту конуса, площадь осевого сечения и основания.
4. Найдите площадь основания и площадь осевого сечения тела, полученного при вращении прямоугольного треугольника с катетом 3см и прилежащим углом 300 вокруг меньшего катета.
5. Радиусы оснований усечённого конуса равны 5дм и 11дм, а образующая равна 10дм. Найдите: а) высоту усечённого конуса; б) площадь осевого сечения.
6. Радиус сферы равен 112см. Точка, лежащая на плоскости, касательной к сфере, удалена от точки касания на 15см. Найдите расстояние от этой точки до ближайшей к ней точки сферы.
7. Угол между высотой цилиндра и диагональю осевого сечения равен 600. Найдите площадь осевого сечения и площадь основания цилиндра, если длина диагонали осевого сечения – 24мм.
8. Высота цилиндра равна 12м. а радиус основания равен 10м. Цилиндр пересечён плоскостью, параллельной его оси, так, что в сечении получился квадрат. Найдите расстояние от оси цилиндра до секущей плоскости.
9. Осевое сечение конуса – прямоугольный треугольник. Найдите площадь этого сечения и высоту конуса, если радиус основания конуса равен 5  см.
10. Найдите площадь основания и площадь осевого сечения тела, полученного при вращении квадрата вокруг одной из сторон. Диагональ квадрата равна 6 см.
10. Найдите площадь основания и площадь осевого сечения тела, полученного при вращении квадрата вокруг одной из сторон. Диагональ квадрата равна 6  см.
11. Радиус основания конуса равен 14м. Найдите площадь сечения, проведённого перпендикулярно его высоте через её середину. см.
11. Радиус основания конуса равен 14м. Найдите площадь сечения, проведённого перпендикулярно его высоте через её середину.
|
12. Найдите площадь сечения шара радиуса 41см, проведённого на расстоянии 9см от центра.
13. На расстоянии 6дм от центра шара проведено сечение, площадь которого равна 64дм2. Найдите радиус шара.
14. Радиусы оснований усечённого конуса равны 1м и2м, высота – 3м. Найдите площадь осевого сечения.
15. Угол между высотой конуса и образующей равен 300. Найдите образующую и площадь осевого сечения конуса, если радиус основания равен 5м.
16. Найдите площадь основания и площадь осевого сечения тела, полученного при вращении равнобедренного прямоугольного треугольника с катетом 6см вокруг его оси симметрии.
17. Площадь основания цилиндра – 5м2, а площадь осевого сечения – 10м2. Найдите высоту цилиндра и диагональ осевого сечения.
18. Высота цилиндра равна 10дм. Площадь сечения плоскостью параллельной оси цилиндра и удалённой на 9дм от неё равна 240дм2. Найдите радиус цилиндра.
19. Образующая конуса равна 25м, а диаметр основания - -48м. Найдите площадь основания и осевого сечения конуса.
20. Осевым сечением цилиндра является квадрат, диагональ которого равна 3 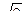 см. Найдите площадь осевого сечения и площадь основания цилиндра.
21. Найдите площадь основания и площадь осевого сечения тела, полученного при вращении прямоугольника со сторонами 34м и 6м вокруг прямой, проходящей через середины его больших сторон.
22. Радиусы оснований усечённого конуса равны 10м и 8м, а образующая составляет с плоскостью основания угол в 450. Найдите площадь осевого сечения.
23. Сферу на расстоянии 8м от центра пересекает плоскость. Радиус сечения равен 15м. Найдите радиус сферы.
24. Диаметр основания цилиндра – 30см. Цилиндр пересечён плоскостью, параллельной его оси, так, что в сечении получился квадрат. Расстояние от оси цилиндра до секущей плоскости – 12см. Найдите площадь сечения. см. Найдите площадь осевого сечения и площадь основания цилиндра.
21. Найдите площадь основания и площадь осевого сечения тела, полученного при вращении прямоугольника со сторонами 34м и 6м вокруг прямой, проходящей через середины его больших сторон.
22. Радиусы оснований усечённого конуса равны 10м и 8м, а образующая составляет с плоскостью основания угол в 450. Найдите площадь осевого сечения.
23. Сферу на расстоянии 8м от центра пересекает плоскость. Радиус сечения равен 15м. Найдите радиус сферы.
24. Диаметр основания цилиндра – 30см. Цилиндр пересечён плоскостью, параллельной его оси, так, что в сечении получился квадрат. Расстояние от оси цилиндра до секущей плоскости – 12см. Найдите площадь сечения.
|
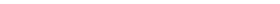 25. Площадь основания цилиндра 16p см2. Угол между образующей цилиндра и диагональю его осевого сечения равен 300. Найдите площадь и диагональ осевого сечения.
26. Цилиндр пересечён плоскостью, параллельной его оси, на расстоянии 5мм. Найдите высоту цилиндра, если диаметр основания – 26мм, а площадь сечения – 240мм.
27. Образующая конуса наклонена к плоскости основания под углом 600. Найдите высоту конуса и площадь осевого сечения , если радиус основания равен 9мм..
28. Найдите площадь основания и площадь осевого сечения тела, полученного при вращении прямоугольника со сторонами 14м и 6м вокруг меньшей стороны.
29. Найдите образующую усечённого конуса, если радиусы оснований равны 3см и 6см, а высота равна 4см.
30. Вершины равностороннего треугольника лежат на сфере радиуса 13см. Найдите расстояние от центра сферы до плоскости треугольника, если сторона треугольника равна 10 25. Площадь основания цилиндра 16p см2. Угол между образующей цилиндра и диагональю его осевого сечения равен 300. Найдите площадь и диагональ осевого сечения.
26. Цилиндр пересечён плоскостью, параллельной его оси, на расстоянии 5мм. Найдите высоту цилиндра, если диаметр основания – 26мм, а площадь сечения – 240мм.
27. Образующая конуса наклонена к плоскости основания под углом 600. Найдите высоту конуса и площадь осевого сечения , если радиус основания равен 9мм..
28. Найдите площадь основания и площадь осевого сечения тела, полученного при вращении прямоугольника со сторонами 14м и 6м вокруг меньшей стороны.
29. Найдите образующую усечённого конуса, если радиусы оснований равны 3см и 6см, а высота равна 4см.
30. Вершины равностороннего треугольника лежат на сфере радиуса 13см. Найдите расстояние от центра сферы до плоскости треугольника, если сторона треугольника равна 10 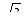 см.
31. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 600. Образующая цилиндра равна 10 см.
31. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 600. Образующая цилиндра равна 10 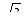 см, расстояние от оси до секущей плоскости равно 2см. Найдите площадь сечения.
32. Площадь основания цилиндра относится к площади осевого сечения как см, расстояние от оси до секущей плоскости равно 2см. Найдите площадь сечения.
32. Площадь основания цилиндра относится к площади осевого сечения как 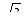 p : 4. Найдите угол между диагоналями осевого сечения.
33. Найдите угол при вершине осевого сечения конуса, если развёрткой его боковой поверхности является сектор с дугой, равной 1800.
34. Вычислите площадь основания и высоту конуса, если развёрткой его боковой поверхности является сектор, радиус которого равен 9см, а дуга равна 1200.
35. Сфера касается граней двугранного угла в 1200. Найдите радиус сферы и расстояние между точками касания, если расстояние от центра сферы до ребра двугранного угла равно а. p : 4. Найдите угол между диагоналями осевого сечения.
33. Найдите угол при вершине осевого сечения конуса, если развёрткой его боковой поверхности является сектор с дугой, равной 1800.
34. Вычислите площадь основания и высоту конуса, если развёрткой его боковой поверхности является сектор, радиус которого равен 9см, а дуга равна 1200.
35. Сфера касается граней двугранного угла в 1200. Найдите радиус сферы и расстояние между точками касания, если расстояние от центра сферы до ребра двугранного угла равно а.
|
| 4.3 ДОПОЛНИТЕЛЬНЫЕ ЗАДАНИЯ |
| 1. В цилиндре диаметром 15мм сделано цилиндрическое отверстие диаметром 5мм. Оси обоих цилиндров совпадают. Затем цилиндр разрезали пополам плоскостью, проходящей через ось. Нарисовать и указать размеры получившегося тела. |
2. От деревянных моделей цилиндра и конуса отпилили по кусочку разной формы, оставшиеся части изобразили на рисунке.
 Нарисуйте развёртку поверхности срезанной части для каждой модели.
3. На поверхности геометрических тел нарисованы различные узоры.
Нарисуйте развёртку поверхности срезанной части для каждой модели.
3. На поверхности геометрических тел нарисованы различные узоры.
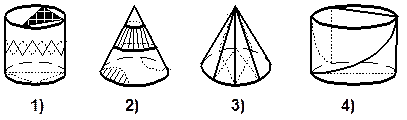 Изобразите развёртки поверхностей этих тел и покажите на них соответствующие узоры.
4. Постройте развёртку поверхности:
1) цилиндра
а) диаметр которого равен 40мм, а высота 5см;
б) в осевом сечении которого лежит прямоугольный треугольник со сторонами 3см и 4см (2 варианта);
в) в осевом сечении которого лежит квадрат с диагональю 6
Изобразите развёртки поверхностей этих тел и покажите на них соответствующие узоры.
4. Постройте развёртку поверхности:
1) цилиндра
а) диаметр которого равен 40мм, а высота 5см;
б) в осевом сечении которого лежит прямоугольный треугольник со сторонами 3см и 4см (2 варианта);
в) в осевом сечении которого лежит квадрат с диагональю 6 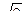 см. см.
|
2) конуса
а) радиусом 3см и образующей 80мм;
б) полученного при вращении прямоугольного треугольника с катетами 0,6дм и 8см (2 вида);
в) в осевом сечении которого лежит равносторонний треугольник со стороной 0, 04м;
г) диаметр которого равен 30мм, а образующая наклонена к плоскости основания под углом 300;
3) усечённого конуса
а) радиусы которого 30мм и 0,5дм, а высота 4см;
б) больший радиус которого равен 0,03м, высота 0,2дм, а образующая наклонена к плоскости основания конуса под углом 300;
в) отношение большего радиуса к меньшему 1: 2 и образующая наклонена к плоскости основания под углом 300.
5. На каждом рисунке выберите основные детали и объясните, почему вы считаете их основными.
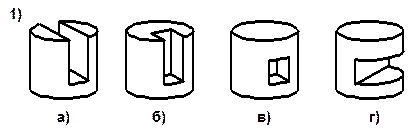
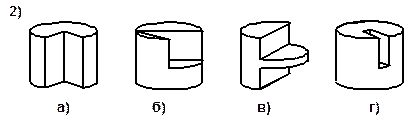 Можно ли из них получить любую другую деталь, изображённую на этом же рисунке?
Можно ли из них получить любую другую деталь, изображённую на этом же рисунке?
|
6. В каждой строке написано пять слов, из которых четыре можно объединить в одну группу и дать ей название, а одно слово к этой группе не относится. Найдите это слово и назовите оставшуюся группу.
1) Образующая, высота, ось, апофема, радиус.
2) Квадрат, треугольник, конус, круг, эллипс.
3) Вершина, конус, цилиндр, пирамида, призма.
4) Ребро, радиус, образующая, высота, диаметр.
5) Грань, ребро, высота, основание, образующая.
7. Перечислите фигуры, изображённые на рисунке.

|
| 5 ПЛОЩАДЬ ПОВЕРХНОСТИ И ОБЪЁМ ТЕЛ ВРАЩЕНИЯ И МНОГОГРАННИКОВ О ПОНЯТИИ ТЕЛА, ЕГО ПОВЕРХНОСТИ И ОБЪЁМА В ГЕОМЕТРИИ |
| Геометрическое тело – часть пространства, обычно ограниченная, то есть принадлежащая, например, некоторому шару. Другими знакомыми нам примерами тел являются многогранник, цилиндр и конус. Поверхность – одно из основных геометрических понятий. В элементарной математике рассматриваются плоскости, многогранные, а также некоторые кривые поверхности. Поверхность - граница тела. |
| Объём – одна из основных величин, связанных с геометрическими телами. В простейших случаях измеряется числом умещающихся в теле единичных кубов, то есть кубов с ребром, равным единице длины. Объём простого тела Тело называется простым, если его можно разбить на конечное число треугольных пирамид. Примером простого тела является любой выпуклый многогранник. Объём – это положительная величина, численное значение которой обладает следующими свойствами: 1. Равные тела имеют равные объёмы. 2. Если тело разбито на части, являющиеся простыми телами, то объём этого тела равен сумме объёмов его частей. 3. Объём куба, ребро которого равно единице длины, равен единице. Два тела называются равновеликими, если они имеют равные объёмы. Объём произвольного тела Данное тело имеет объём V, если существуют содержащие его простые тела и содержащиеся в нём простые тела с объёмами, сколь угодно мало отличающимися от V. Современная трактовка измерения объёмов сводится к следующему. Рассматриваются всевозможные многогранники, вписанные в тело К, и всевозможные многогранники, описанные вокруг тела К. Вычисление объёма многогранника сводится к вычислению объёмов, составляющих его тетраэдров. |
ПЛОЩАДЬ ПОВЕРХНОСТИ И ОБЪЁМ Дата: 2018-12-21, просмотров: 1939. |

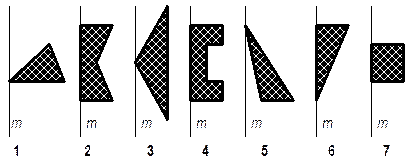
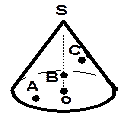
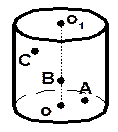
 см. Найдите площадь осевого сечения и площадь основания цилиндра.
см. Найдите площадь осевого сечения и площадь основания цилиндра.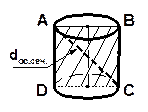
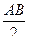 = 4
= 4 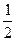 ah =
ah = 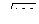 = 6
= 6 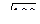 = 10(дм) Þ Rш. = 10дм.
= 10(дм) Þ Rш. = 10дм.