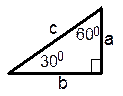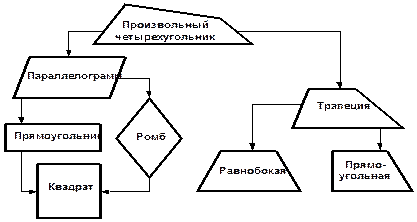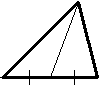
Медиана - отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
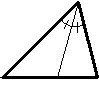
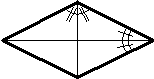
Биссектриса - отрезок, который соединяет вершину треугольника с точкой на противолежащей стороне и делит внутренний угол пополам.
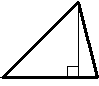
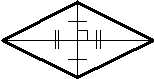
Высота - перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противолежащую сторону треугольника.
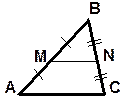
Средняя линия - отрезок, соединяющий середины двух сторон треугольника.
Свойство средней линии
Средняя линия параллельна одной из сторон и равна её половине:
MN || АС, MN= 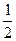 AC.
AC.
|
ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК | |
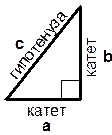
| Теорема Пифагора. Сумма квадратов катетов равна квадрату гипотенузы: a2 + b2 = c2. Следствия из теоремы: a2 = c2 – b2, b2 = c2 – a2 |
| Соотношение между сторонами и углами в прямоугольном треугольнике |
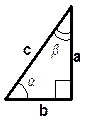
| Синус: sin Косинус: cos
| |||
| Тангенс: tg | ||||
|
Частные случаи прямоугольных треугольников | ||||
|
| a = 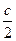  b =
b = 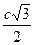 . .
| 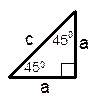
| a = 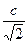 c =
c = 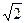
| |
|
ЧЕТЫРЁХУГОЛЬНИКИ | ||||||||
|
ОСНОВНЫЕ ВИДЫ ЧЕТЫРЕХУГОЛЬНИОВ | ||||||||
|
| ||||||||
|
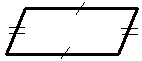
ПАРАЛЛЕЛОГРАММ Так называются четырехугольник, у которого противолежащие стороны параллельны. | ||||||||
|
Свойства Параллелограмма | Признаки параллелограмма | |||||||
| 1. В параллелограмме противоположные углы равны.
2. В параллелограмме противоположные стороны равны.
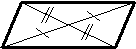
3. Диагонали параллелограмма точкой пересечения делятся пополам.
| 1. Если в четырёхугольнике две противоположные стороны равны и параллельны, то этот четырёхугольник - параллелограмм. 2. Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник - параллелограмм. 3. Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник - параллелограмм. | |||||||
|
РОМБ Так называются параллелограмм, у которого все стороны равны. | ||||||||
|
Свойства ромба |
Признаки ромба | |||||||
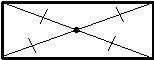
| 1. Диагонали ромба пересекаются под прямым углом. | 1. Если диагонали параллелограмма пересекаются под прямым углом, то этот параллелограмм – ромб. | |||||||
|
| ||||||||
|
Свойства ромба |
Признаки ромба | |||||||
| 2. Диагонали ромба являются биссектрисами его углов. | 2. Если диагонали параллелограмма являются биссектрисами его углов, то этот параллелограмм – ромб. | |||||||
|
| ||||||||
| Все свойства параллелограмма верны для ромба | ||||||||
|
ПРЯМОУГОЛЬНИК Так называется параллелограмм, у которого все углы прямые. | ||||||||
|
Свойства прямоугольника |
Признаки прямоугольника | |||||||
|
Диагонали прямоугольника равны. |
Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник. | |||||||
|
| ||||||||
|
Все свойства параллелограмма верны для прямоугольника | ||||||||
|
КВАДРАТ Так называется прямоугольник, у которого все стороны равны. | ||||||||
Дата: 2018-12-21, просмотров: 836. | ||||||||
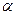 =
= 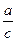 =
= 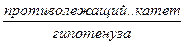 .
.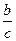 =
= 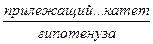 .
.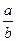 =
= 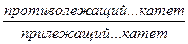 .
.