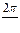НАГЛЯДНОЕ ПОСОБИЕ
ПО ГЕОМЕТРИИ
Учебное пособие для старшеклассников
Северск 2015
| УТВЕРЖДАЮ Зам. директора по НУМР ___________Г.В. Скорик ____ ____________2015 г. | УТВЕРЖДЕНО ОМС ___ ________2015г. |
Рецензенты: М.С. Бухтяк, к.ф.-м. н., доц.;
В.Е. Шутеева, отличник просвещения,
засл. учитель России, учитель-методист.
Авторы:
Поликарпова Н. С. преподаватель,
Сазанова Т. А., заведующий кафедрой естественно математического образования ТОИПКРО, канд. техн. наук, доцент.
Наглядное пособие по геометрии. - Учебное пособие. 2-е изд., испр. и доп. Северск, 2015. - 120 с.
Учебное пособие предназначено для обучающихся средней школы, оно призвано помочь усвоить курс геометрии. Может быть полезно абитуриентам, студентам профессиональных образовательных организаций, преподавателям при изучении, систематизации и повторении курса планиметрии. Особенностью пособия является наглядность во всех видах заданий. Пособие активизирует самостоятельную деятельность обучающихся, допускает дифференцированный подход в обучении и может быть использовано в предпрофильных и профильных классах.
Рассмотрено на заседании цикловой комиссии
Общеобразовательных дисциплин
Протокол № 8 от «14» марта 2015 г.
Председатель цикловой комиссии Журова К.А.
Нормоконтроль: Лазуткина М.Г.
ВВЕДЕНИЕ
"Посредством глаза, но не глазом
смотреть на мир умеет разум"
Уильям Блейк
Своеобразие геометрии, которое выделяет ее из других разделов математики, да и всех областей науки вообще, заключается в неразрывном, органическом соединении живого воображения со строгой логикой. В своей сущности и основе геометрия и есть пространственное воображение, пронизанное и организованное строгой логикой. В ней всегда присутствуют эти два неразрывно связанных элемента - наглядная картина и точная формулировка, строгий логический вывод. Там, где нет одной из этих сторон, нет и подлинной геометрии.
Так писал о геометрии академик А.Д. Александров.
Наглядность, воображение принадлежат больше искусству, строгая логика - привилегия науки. Сухость точного вывода и живость наглядной картины - «лёд и пламень не столь различны меж: собой». Геометрия соединяет в себе эти противоположности, они в ней взаимно проникают, организуют и направляют друг друга. Это относится, в конечном счете, также к современным абстрактным геометрическим теориям, которые при всей своей возвышенной отвлеченности вырастают из той же геометрической интуиции. Стоит лишь вспомнить классические творения архитектуры, начиная с древнейших пирамид, как сразу становится очевидным, что геометрия в некотором смысле относится к искусству.
При изучении геометрии особое внимание уделяется развитию визуального мышления учащихся.
Основное правило состоит в том, что, встречаясь с определением, теоремой или задачей, необходимо, прежде всего, представить соответствующую геометрическую фигуру, сделать рисунок - это поможет понять содержание.
Каждому учителю математики хорошо знакомы те трудности, с которыми сталкивается школьник при переводе геометрической задачи на язык чертежа, он часто не может сделать рисунок или запомнить название фигуры, её элементов. Поэтому необходимы специальные приемы для формирования соответствующих умений у учащихся.
Основной задачей преподавателя является оказание помощи в переводе знаковой информации в визуальную, в создании образа данного знака, фигуры, рисунка.
Образ, как известно из психологии, - это помощник мысли, который облегчает понимание новых сложных объектов.
Если учащемуся предложить материал неизвестного ему содержания и непривычного оформления, то он не воспримет, не увидит ничего. Нельзя видеть, не понимая; слово "видеть" имеет два значения: зрительно воспринимать что-либо и понимать что-либо.
Известно, что степени "понимания" могут быть весьма различны: от смутного ощущения до полной ясности.
Значит, для того чтобы оптимизировать процесс усвоения материала, учителю необходимо растолковать ученику, как именно и в каком порядке он может рассматривать данный материал, чтобы иметь хотя бы относительную ясность, т. е. помочь ученику в поиске порядка в беспорядочности.
Как облегчить обучающемуся проникновение в содержание, значение предъявляемых зрительных образов?
При формировании первичного образа большое внимание уделяется качеству его изображения. Нельзя научить геометрии, показывая безграмотное оформление рисунков к задачам и теоремам. Образ должен быть сформирован и организован разумно, чтобы наиболее важные его свойства были ясно видимы.
Для дальнейшего формирования образа и развития визуального мышления необходима особая организация материала. Специальное расположение чертежей, графиков, формул позволяет ученику выстраивать их в системы, сравнивать визуальные комбинации с некоторым обобщённым образом. Это способствует развитию зрительных ориентиров (визуальных стандартов), которые в дальнейшем помогут в решении задач.
Активное и целенаправленное использование визуального мышления в процессе обучения основано на выработке устойчивых стандартных образов основных учебных понятий. Подготовка добротных геометрических изображений этих понятий, адекватно отражающих их основные черты, удобных в работе, пригодных для многократного использования, является первостепенной задачей.
Не следует стараться что-то заучить, не нарисовав, не вообразив того, о чём идёт речь. Поэтому каждая тема в предлагаемом пособии снабжена наглядным материалом, направленным на усвоение теории. Это способствует развитию образного мышления обучающихся, обогащает их представления о свойствах геометрических фигур, обеспечивает качество обучения.
Учебное пособие состоит из 6 разделов, каждый из которых включает в себя наглядный теоретический материал, подборку упражнений для закрепления, решение основных задач, задачи разного уровня и рисунки к ним.
Теоретический материал содержит основные определения, свойства, теоремы и формулы, необходимые в решении задач. Доказательство теорем опускается.
В разделе "Планиметрия" собран теоретический материал, необходимый для решения стереометрических задач. Целью этого раздела является изображение рисунков и изложение теории наглядно, доступно и в разумном порядке, для правильного формирования первичного образа.
Упражнения, представленные в каждом разделе, направлены на закрепление теоретического материала. Все они снабжены рисунками. Таким образом, формируется визуальный стандарт, который в дальнейшем помогает ученику в решении задач.
В каждом разделе предложено оформление и решение основных типов задач по теме. Все предложенные задачи соответствуют нескольким уровням усвоения знаний, причем сначала предложены рисунки к задачам, а затем в произвольном порядке условия к ним. Это сделано для того, чтобы ученик выбрал необходимый рисунок к задаче, а также обратил внимание на различное изображение фигур.
Под чертой даны задачи II-III уровня сложности. Из задач этого раздела можно составить разноуровневые контрольные работы.
В процессе решения ученику предлагаются готовые рисунки (номера задач и рисунков не совпадают). Это сделано для того, чтобы обучающиеся на первых порах не испытывали трудности в построении рисунка и привыкали к правильному изображению. Как только у обучающихся сформируется устойчивый визуальный образ (стандарт), необходимость обращения к данным рисункам отпадает.
Для развития творческих способностей ученику необходимо представить данный образ в нестандартной ситуации. Этой цели посвящены дополнительные задания в конце каждого раздела. Они направлены на развитие не только пространственного воображения, но и других интеллектуальных качеств. Ученик сам сможет выбрать интересующее его задание и тем самым расширить свои знания по данной теме.
На уроках геометрии для развития визуального мышления необходимо использовать игры, упражнения, тесты, развивающие внимание, наблюдательность, воображение и память. Задания развивающего характера также можно найти в пособии. В приложении даны развёртки, по которым обучающиеся смогут изготовить модели фигур.
Данное пособие призвано обеспечить дифференцированный подход к обучению, его можно использовать для организации самостоятельной и индивидуальной работы, для контроля знаний.
Особенность данного пособия в том, что здесь предложена система упражнений и заданий, направленных на развитие индивидуальных интеллектуальных возможностей обучающихся.
СОДЕРЖАНИЕ
1 Планиметрия. 9
1.1 Прямые и углы на плоскости. 9
1.2 Треугольники. 11
1.3 Четырёхугольники. 14
1.4 Окружность. 17
1.5 Основные формулы.. 19
1.6 Задачи. 22
2 Стереометрия. 27
2.1 Прямые и плоскости в пространстве. 27
2.2 Параллельность прямых и плоскостей. 30
2.3 Упражнения. 32
2.4 Задачи. 41
2.5 Дополнительные задания. 43
2.6 Перпендикулярность прямых и плоскостей. 47
2.7 Упражнения. 52
2.8 Задачи. 59
2.9 Дополнительные задания. 62
3 Многогранники. 65
3.1 Упражнения. 71
3.2 Задачи. 81
3.3 Дополнительные задания. 85
4 Тела вращения. 90
4.1 Упражнения. 93
4.2 Задачи. 98
5 Площадь поверхности и объём тел вращения и многоранников 103
5.1 Упражнения. 106
5.2 Задачи. 107
5.3 Дополнительные задания. 113
Приложения. 115
Ответы.. 118
Список литературы.. 120
ПЛАНИМЕТРИЯ
Так называется раздел геометрии, в котором изучаются фигуры
на плоскости.
ПРЯМЫЕ И УГЛЫ НА ПЛОСКОСТИ
ВИДЫ УГЛОВ
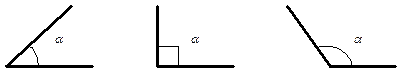 Острый угол Прямой угол Тупой угол
Острый угол Прямой угол Тупой угол
00 < a < 900 . a = 900 . 900 < a< 1800.
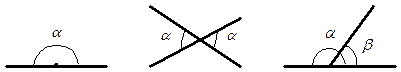 Развернутый угол Вертикальные углы Смежные углы
Развернутый угол Вертикальные углы Смежные углы
a = 1800. равны. a + b = 1800.
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
Так называются прямые, которые не пересекаются.
Теорема Фалеса
Если параллельные прямые, пересекающие стороны угла, отсекают на одной стороне угла равные отрезки, то они отсекают равные отрезки и на другой стороне угла.
Верно и обратное: если некоторые прямые, не пересекающиеся внутри угла, отсекают на одной стороне угла равные между собой отрезки и на другой стороне тоже равные между собой
отрезки, то такие прямые параллельны.
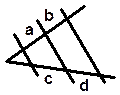
Параллельные прямые, пересекающие стороны угла, отсекают на сторонах угла пропорциональные отрезки:
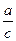 =
= 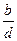 .
.
ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ
Так называются прямые, которые пересекаются под прямым углом.
Перпендикуляр и наклонная
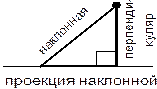
Перпендикуляр короче любой наклонной, проведенной к прямой из той же точки.
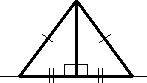
У равных наклонных, проведенных из одной и той же точки, проекции равны. Верно и обратное: если проекции равны, то и равны их
наклонные.
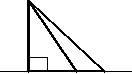
Из двух наклонных, проведенных из одной и той же точки, больше та, у которой проекция больше.
Верно и обратное.
|
ТРЕУГОЛЬНИКИ | ||||
|
ВИДЫ ТРЕУГОЛЬНИКОВ | ||||
|
Остроугольный Тупоугольный Прямоугольный (все углы острые). (один угол тупой). (один угол равен 900).
(нет равных сторон) (две стороны равны) (все стороны равны) Ð1 = Ð2 Ð1 = Ð2 = Ð3=600 | ||||
|
В треугольнике | ||||
|
|
Сумма углов треугольника равна 1800: a+b+g =1800. Против большей стороны лежит больший угол: b > a Û b > a. | |||
| Теорема синусов:
где R – радиус описанной окружности около треугольника. Теорема косинусов: c2 = a2 + b2 –2ab cos g. | ||||
|
Свойство средней линии Средняя линия параллельна одной из сторон и равна её половине: MN || АС, MN= | ||||
|
ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК | |
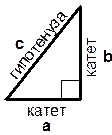
| Теорема Пифагора. Сумма квадратов катетов равна квадрату гипотенузы: a2 + b2 = c2. Следствия из теоремы: a2 = c2 – b2, b2 = c2 – a2 |
| Соотношение между сторонами и углами в прямоугольном треугольнике |
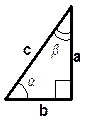
| Синус: sin Косинус: cos
| ||||||||
| Тангенс: tg | |||||||||
|
ЧЕТЫРЁХУГОЛЬНИКИ | |||||||||
|
ПАРАЛЛЕЛОГРАММ Так называются четырехугольник, у которого противолежащие стороны параллельны. | |||||||||
|
Свойства Параллелограмма | Признаки параллелограмма | ||||||||
| 1. В параллелограмме противоположные углы равны.
2. В параллелограмме противоположные стороны равны.
3. Диагонали параллелограмма точкой пересечения делятся пополам.
| 1. Если в четырёхугольнике две противоположные стороны равны и параллельны, то этот четырёхугольник - параллелограмм. 2. Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник - параллелограмм. 3. Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник - параллелограмм. | ||||||||
|
РОМБ Так называются параллелограмм, у которого все стороны равны. | |||||||||
|
Свойства ромба |
Признаки ромба | ||||||||
| 1. Диагонали ромба пересекаются под прямым углом. | 1. Если диагонали параллелограмма пересекаются под прямым углом, то этот параллелограмм – ромб. | ||||||||
|
| |||||||||
|
Свойства ромба |
Признаки ромба | ||||||||
| 2. Диагонали ромба являются биссектрисами его углов. | 2. Если диагонали параллелограмма являются биссектрисами его углов, то этот параллелограмм – ромб. | ||||||||
|
| |||||||||
| Все свойства параллелограмма верны для ромба | |||||||||
|
ПРЯМОУГОЛЬНИК Так называется параллелограмм, у которого все углы прямые. | |||||||||
|
Свойства прямоугольника |
Признаки прямоугольника | ||||||||
|
КВАДРАТ Так называется прямоугольник, у которого все стороны равны. | |||||||||
|
ТРАПЕЦИЯ Так называется четырехугольник, у которого две стороны параллельны (основания), а две другие – не параллельны (боковые стороны). | |||||||||
|
| |||||||||
| Свойства трапеции | |||||||||
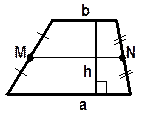
| Средняя линия параллельна основаниям, равна их полусумме и делит любой отрезок с концами, лежащими на прямых, содержащих основания, (например, высоту трапеции) пополам: MN || a, MN || b, MN = | ||||||||
| Сумма углов, принадлежащих к любой боковой стороне, равна 1800:
| ||||||||
|
ОКРУЖНОСТЬ Так называется фигура, которая состоит из всех точек плоскости, равноудалённых от данной точки. Эта точка называется центром окружности Часть плоскости, ограниченная окружностью, называется Кругом | |||||||||
|
Радианная мера угла Угол в один радиан равен центральному углу, опирающемуся на дугу, длина которой равна радиусу окружности | |
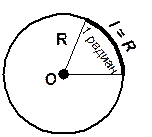
| Радианной мерой угла называется отношение длины соответствующей дуги к радиусу окружности.
1 радиан » 57017¢ 45¢¢,
10 =  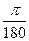 радиан.
p радиан -1800,
p радиан.
p радиан -1800,
p  3,14 радиан. 3,14 радиан.
|
|
ОСНОВНЫЕ ФОРМУЛЫ | |||
|
Наименование |
Формулы для вычисления | ||
| Периметра | Площади | Радиуса | |
| 1 | 2 | 3 | 4 |
Треугольник
1. Произвольный
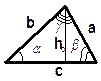 2. Равносторонний
(правильный)
2. Равносторонний
(правильный)
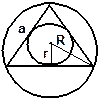 3. Прямоугольный
3. Прямоугольный
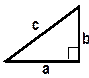
| P =a+b+c P = 3×a P =a+b+ с | S =  hC × c, S= hC × c, S=  b × c × sin a ,
Формула Герона:
S= b × c × sin a ,
Формула Герона:
S= 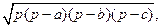 где p = где p = 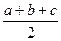 .
S = p × r; S = .
S = p × r; S = 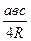 S =
S = 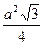 S =
S = 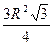 ;
S = 3r2 ;
S = 3r2 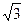 S =
S =  a × b a × b
|
a=R 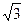 a=2r
a=2r 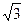 R=
R= 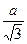 ,
r= ,
r= 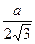 r =
r =  R, R=2r R, R=2r
|
| 1 | 2 | 3 | 4 |
Четырёхугольник
1. Параллелограмм
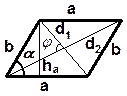 2. Ромб
2. Ромб
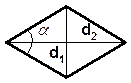 3. Прямоугольник 3. Прямоугольник
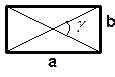 4. Квадрат
4. Квадрат
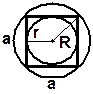 5. Трапеция
5. Трапеция
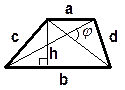
| P = 2(a +b) P = 4a P = 2(a +b) P = 4a P=a+b+c+d |
S = a × b × sin a ,
S = a × h a ,
S =  d1d2 sin j
S = a2 × sin a ,
S = d1d2 sin j
S = a2 × sin a ,
S =  d 1 × d 2
S = a×b
S = d 1 × d 2
S = a×b
S =  d2sin g
S = a2
S = d2sin g
S = a2
S =  d2
S = d2
S =  (a + b)h
S = (a + b)h
S =  d1d2sin j d1d2sin j
|
a=R  a=2 × r
R= r a=2 × r
R= r  r=
r= 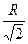
|
|
Площадь круга и его частей | ||
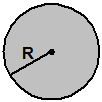 Площадь круга:
S = p R 2 .
Площадь круга:
S = p R 2 .
|
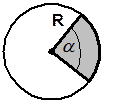 Площадь сектора:
S =
Площадь сектора:
S =  a R 2
(угол в радианах). a R 2
(угол в радианах).
|
 Площадь сегмента:
S =
Площадь сегмента:
S =  ( a – sin a ) R 2
(угол a в радианах). ( a – sin a ) R 2
(угол a в радианах).
|
|
Длина дуги и окружности | |
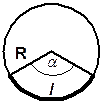 Длина дуги:
l = a R
(угол a в радианах).
Длина дуги:
l = a R
(угол a в радианах).
|  Длина окружности:
L = 2 p R .
Длина окружности:
L = 2 p R .
|
|
ЗАДАЧИ ТРЕУГОЛЬНИК | ||||||||||
|
ЧЕТЫРЁХУГОЛЬНИК Найдите периметр.
Найдите площадь.
ДОПОЛНИТЕЛЬНЫЕ ЗАДАНИЯ | ||||||||||
| 1. Сколько всего треугольников изображено на рисунке. | ||||||||||
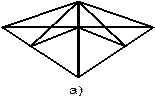
|
| |||||||||
| 2. Найдите площадь заштрихованной фигуры. | ||||||||||
|
а) б) в) г) д) е)
3. Разрежьте тупоугольный треугольник на остроугольные треугольники.
4. Разрежьте остроугольный равнобедренный треугольник на четыре одинаковых равнобедренных треугольника, подобных исходному. 5. Отец красавицы Лолиты, живший в древней Индии, назойливым женихам давал несколько заданий. И лишь тот, кто выполнял эти задания, мог претендовать на ее руку. Вот одно из них: скажи, сколько треугольников нарисовано на полу в центральном зале?
6. На берегу священной реки Ганг жил знаменитый брахман Радж. Он обнес свой замок глубоким рвом, наполненным водой. И только тот мог попасть в замок, кто с помощью двух дощечек, длина которых меньше ширины рва, не замочив ног, переходил ров. Попробуй и ты побывать в гостях у Раджи. | ||||||||||
|
СТЕРЕОМЕТРИЯ Так называется раздел геометрии, в котором изучаются фигуры в пространстве. АКСИОМЫ СТЕРЕОМЕТРИИ | ||||||||||
С1
 A Î a, M Ï a
A Î a, M Ï a
| Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей. | |||||||||
С2
 a
a  b = а b = а
| Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку. | |||||||||
| C3
|
Если две различные прямые имеют общую точку, то через них можно провести плоскость и притом только одну. | ||
|
Взаимное расположение | |||
| Прямой и плоскости |
Двух плоскостей | ||
а  a = А а ^ a a = А а ^ a
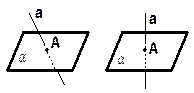 Прямая и плоскость пересекаются, если у них только одна общая точка.
Прямая и плоскость пересекаются, если у них только одна общая точка.
| a
Две плоскости пересекаются, если множество их общих точек есть прямая. | ||
|
Двух плоскостей | ||
а || g
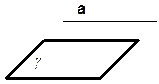 Прямая и плоскость параллельны, если они не имеют общих точек.
Прямая и плоскость параллельны, если они не имеют общих точек.
| j || m
Две плоскости параллельны, если не имеют общих точек. | |
|
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ Так называются прямые, которые лежат в одной плоскости и не пересекают её. | ||
|
ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ Так называются плоскости, которые не пересекаются (не имеют общих точек).
| ||
|
УПРАЖНЕНИЯ | ||
| 1. По рисунку ответьте на вопросы. | ||
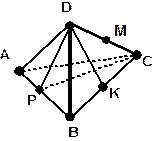
| 1. Каким плоскостям принадлежит точка: А, М, К, D, Р? 2. Вне каких плоскостей лежит точка: М, К, А, Р, D? 3. На каких плоскостях лежат прямые: DB, DK, АВ, РС, АС? 4. В какой точке пересекаются прямая и плоскость: а) AD и АВС; | |
| б) BD и ADC; в) DK и АВС; г) РС и ADB; д) AD и PDC? 5. По какой прямой пересекаются плоскости: а) АВD и BDC; б) АВС и ADC; в) АВС и АВD; г) ABD и АDC; д) PDC и АВС? 6. Какие прямые лежат на плоскостях: а) АВС; б) ABD; в) BDC? | ||
| 2. Сколько плоскостей можно провести через выделенные элементы куба? Заштрихуйте соответствующие плоскости грани куба.
3. Сколько граней проходит через: а) одну, б) две, в) три, г) четыре точки, выделенные на рисунке куба? Сколько плоскостей можно провести через те же точки? Определится ли при этом положение плоскости однозначно?
4. ABCDA1B1C1D1 – куб. | ||
|
| 1. Перечислите все ребра: а) пересекающие ребро DD1; б) параллельные ребру АD; в) скрещивающиеся с ребром DC. 2. Запишите как располагаются прямые: а) АD1 и D1C1; б) AD1 и ВС1; в) AD1 и СС1; г) AD1 и BC1; д) AD1 и В1С1. | |
| 3. Найдите точки пересечения прямых: а) DC и СС1; б) DC и D1P; в) ВР и В1С1; г) AD1 и D1P. 4. Найдите: а) ребра, параллельные с DD1 и пересекающиеся с С1В1; б) ребра, скрещивающиеся с АВ и пересекающие D1C1; в) ребро, параллельное DC и скрещивающееся с D1A1.
| ||
| 5. MNPQM 1 N 1 P 1 Q 1 – наклонный параллелепипед | ||
|
| По рисунку перечислите: 1. все видимые грани; 2. все невидимые грани; 3. попарно параллельные прямые в плоскости видимого основания; 4. попарно параллельные прямые в плоскости видимой боковой грани; | |
| 5. попарно параллельные прямые в плоскости невидимого основания; 6. попарно параллельные прямые в плоскости невидимой боковой грани; 7. пару пересекающихся прямых в плоскости видимого основания; 8. пару пересекающихся прямых в плоскости невидимого основания; 9. пару пересекающихся прямых в плоскости видимой боковой грани; 10. пару пересекающихся прямых в плоскости невидимой боковой грани; 11. пару скрещивающихся прямых, одна из которых лежит в плоскости видимого основания; 12. пару скрещивающихся прямых, одна из которых лежит в плоскости невидимого основания; | ||
| 6. ABCDA 1 B 1 C 1 D 1 – прямой параллелепипед. | ||
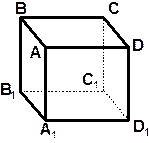
| 1. Выпишите все попарно параллельные грани. 2. По каким прямым пересекаются: а) плоскости АВС и А1В1С1 с плоскостями А1АD и В1ВС? б) плоскости АВВ1 иDCC1 с плоскостями А1АD иВ1ВС? Как расположены между собой эти прямые пересечения плоскостей? Ответ обоснуйте. | |
| 7. ABCDA 1 B 1 C 1 D 1 – куб. | ||||
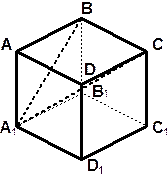
| 1. По каким прямым пересекаются плоскости: а) А1ВС и АВС; б) А1ВС и А1В1С1; в) А1ВС и АВВ1; г) А1ВС тDCC1? Перерисуйте чертеж в тетрадь и проведите недостающие прямые. 2. Как попарно расположены найденные прямые пересечения плоскостей? Ответ обоснуйте. | |||
|
ИХ РЕШЕНИЕ | ||||
| 1. Через концы отрезка АВ и его середину М проведены параллельные прямые, пересекающие некоторую плоскость в точках А1, В1 и М1. Найдите длину отрезка ММ1, если АА1 = 3,6 дм, ВВ1 = 4,8 дм. | ||||
Дано:
АВ,  ;
М ;
М  АВ;
АМ= МВ;
А1, М1, В1 АВ;
АМ= МВ;
А1, М1, В1  a;
АА1| | DD1| | ММ1;
АА1= 3,6см;
ВВ1= 4,8см.
Найти: ММ1. a;
АА1| | DD1| | ММ1;
АА1= 3,6см;
ВВ1= 4,8см.
Найти: ММ1.
|
| Решение:
1) Если АА1||ВВ1||ММ1- то эти отрезки лежат в одной плоскости b(по свойству параллельных прямых).
b  a=А1В1. a=А1В1.
| ||
| 2) По теореме Фалеса М1 - середина АВ, тогда ММ1 - средняя линия трапеции АА1В1ВÞ по свойству средней линии трапеции ММ1= Ответ: ММ1 = 4,2см.
| ||||
| Примерный план решения задач первого типа 1. Провести плоскость через: две параллельные прямые; две пересекающиеся прямые; треугольник, трапецию. 2. Применяя теорему Фалеса, признак параллельности прямой и плоскости доказать, что дана средняя линия треугольника (трапеции). 3. Используя свойство средней линии треугольника (трапеции) найти неизвестные величины. 2. Точки М, Н, К, Р–середины соответственно отрезков А D , DС, ВС, АВ. Найдите периметр четырёхугольника МНКР, если МР = 8дм., АС =32дм. | ||||
| Дано: [АD],[DС],[ВС],[АВ]; МÎАD, АМ= МD; НÎDС, DН=НС; РÎАВ, АР= РВ; КÎ ВС, ВК= КС; МР= 8дм., АС= 32дм. Найти: РМНКР. | 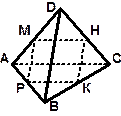
| Решение: 1) АВСD пространственный четырёхугольник (его вершины не лежат в одной плоскости) и М, Н, К, Р- середины его сторон (кроме АС). | ||
| 2) РМ - средняя линия DАВD (по условию) ÞРМ|| ВD; НК - средняя линия DСDВÞНК|| ВD, значит по признаку параллельности прямых РМ|| НК, тогда четырёхугольник РМНК лежит в одной плоскости. МН - средняя линия DАDС и РК- средняя линия DАВСÞМН|| АС и РК||АС, тогда МН|| РК, значит РМНК – параллелограмм 3) РМНКР = 2(РМ+МН). По свойству средней линии треугольника МН= Ответ: РМНКР.=48дм.
| ||||
Примерный план решения задач второго типа 1.Дан пространственный четырёхугольник (его вершины не лежат в одной плоскости). Указать точки, которые являются серединами его сторон. 2. Применяя признак параллельности прямых в пространстве и свойство средней линии треугольника, доказать, что фигура, лежащая внутри пространственного четырёхугольника – параллелограмм. 3. Применяя свойства средней линии треугольника и параллелограмма, найти неизвестные величины. 3. Дан треугольник АВС. Плоскость, параллельная прямой АВ, пересекает сторону АС этого треугольника в точке А1, а сторону ВС – в точке В1. Найдите длину отрезкаА1В1, если В1С = 10см., АВ/ВС = 4/5. | ||
Дано:
DАВС, a||АВ;
a  АС = А1;
a АС = А1;
a  ВС = В1;
В1С = 10см.;
АВ/ВС = 4/5.
Найти: А1В1. ВС = В1;
В1С = 10см.;
АВ/ВС = 4/5.
Найти: А1В1.
| 
| Решение:
1) Пусть DАВС лежит в плоскости g, тогда g 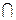 a = А1В1.
А1В1Îa и a||АВÞ А1В1||АВ (по признаку параллельности прямой и плоскости). a = А1В1.
А1В1Îa и a||АВÞ А1В1||АВ (по признаку параллельности прямой и плоскости).
|
| 2) DАВС ¥ DА1В1С по второму признаку подобия треугольников (ÐАСВ – общий, ÐСВ1А1 = ÐСВА как односторонние углы при параллельных прямых АВ и А1В1). 3) | ||
| Примерный план решения задач третьего, Четвёртого и пятого типов 1. Провести плоскость через: треугольник, две пересекающиеся прямые. Указать линию (линии) пересечения плоскостей. Доказать параллельность необходимых сторон. 2. Записать подобные треугольники, признак, обоснование. 3. Записать пропорциональность сторон подобных треугольников. Подставить известные величины и найти неизвестные. | ||
|
РИСУНКИ К ЗАДАЧАМ | ||
|
Примечание: дугой обозначены известные, неизвестные величины знаком "?". | ||
| 2.4 ЗАДАЧИ |
| 1. Точка С лежит на отрезке АВ. Через точку А проведена плоскость , а через точки В и С – параллельные прямые, пересекающие плоскость соответственно в точках В1 и С1. Найти длину отрезка СС1, если точка С – середина отрезка АВ и ВВ1=7м. 2. Точка М, Н, Р и К – середины соответственно отрезков АD, DС, АВ и ВС; РК || МН. Найти периметр четырехугольника МНКР, если АС=8дм., ВD=10дм. 3. На сторонах АВ и АС треугольника АВС взяты соответственно точки D и Е так, что DЕ = 5см., а ВD / DА =2/3. Плоскость a проходит через точки В и С и параллельна отрезку ДЕ. Найдите длину отрезка ВС. 4. Точка А - середина отрезка МР, а точки В, С, D лежат соответственно на отрезках КР, КН, МН. ВС || РН, АD || РН, АВ || СD. Найдите РН, если АВ=4дм., а периметр четырехугольника АВСD равен 28 дм. 5.Плоскоть, параллельная основаниям трапеции, пересекает стороны АВ и СD в точках М и К соответственно, АD=10м., ВС=6м. Найти МК, если М-середина отрезка АВ. 6. Точки М, N, Q и Р - середины отрезков DВ и DС, АС и АВ. Найти периметр четырехугольника MNQP, если АD=12мм., ВС=14мм. 7. Точка С лежит на отрезке АВ. Через точку А проведена плоскость, а через точки В и С- параллельные прямые, пересекающие эту плоскость соответственно в точках В1 и С1. Найдите длину отрезка СС1, если АC/СВ=3/2 и ВВ1=20м. 8. Дан треугольник АВС. Плоскость, параллельная прямой АВ, пересекает сторону АС в точке К, а сторону ВС - в точке М. Найти длину отрезка АВ, если длина КС =12дм., АС=24дм., КМ=9дм. 9. Параллельные плоскости a и b пересекают сторону АВ угла ВАС соответственно в точках А1 и А2 , а сторону АС этого угла – соответственно в точках В1 и В2. Найти АА2 и АВ2, если А1А2=2А1А, А1А2=12м., АВ1=5м. 10.Точки D, С, В лежат соответственно на отрезках МК, МН, РН. Точка А – середина отрезка РК, АВ||СD, ВС||АD, ВС||РМ, СD||НК. Найти РМ и НК, если СD=16мм., ВС=8мм. 11.Через концы отрезка АВ и его середину М проведены параллельные прямые, пересекающие некоторую плоскость в точках А1, В1 и M1. Найдите длину отрезка MM1, если AA1=5 см, BB1=7 см. |
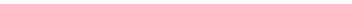 12. Через точку К проведены две прямые a и b, пересекающие две параллельные плоскости a и b: первую в точках А1 и А2, вторую в точках В1 и В2 соответственно. Вычислить КА1 и КВ2, если:
а) А1А2/В1В2=3/4, А1В1=7дм, КА2=12дм;
б) А1А2/ В1В2=1/6, А2В2=3см, В1К=12см.
Точка К не лежит между плоскостями a и b.
13.В треугольнике АВС АВ=15м., АС=24м. Через точку М на стороне АВ, находящейся на расстоянии 10м от точки А, проведена плоскость, параллельная прямой АС и пересекающая сторону ВС в точке К. Найдите длину отрезка МК.
14. Плоскость, параллельная стороне АВ треугольника АВС, пересекает его стороны в точках М и К. Найти АВ, если М- середина стороны АС и МК=10мм.
15. Параллельные плоскости a и b пересекают стороны угла АВС в точках А1, С1, А2, С2 соответственно. Найти ВС1, если А1В/А1А2=1/3, ВС2=12мм.
16. Точка К лежит между параллельными плоскостями a и b. Прямые а и b, проходящие через точку К, пересекают плоскость a в точках А1 и В1, а плоскость b в точках А2 и В2 соответственно. Найти КВ1, если:
а) А1К/А1А2=1/3, В1В2=15м.;
б) В1А1/В2А2=4/6, КВ2=8дм;
в) А2К/А1А2=2/5, В1В2=20см;
г) КВ2/А1В1=1/6, А2В2=2мм.
17. Треугольник АРD и трапеция АВСD имеют общую сторону АD и лежат в разных плоскостях. Через основание ВС трапеции и середину отрезка РD – точку К проведена плоскость, которая пересекает прямую АР в точке М. Найти МК, если АД=10м.
18. Через точку А стороны КМ треугольника КМР проведена плоскость, параллельная прямой МР. Вычислить длину отрезков, на которые делится эта плоскость сторону КР, если МК=10см., МА=6см, КР=15дм.
19. Треугольники АВС и DВС не лежат в одной плоскости и имеют общую сторону; точки М, Н, К- середины соответственно сторон ВD, DС, АС. Отрезок АВ пересекает плоскость МКН в точке Р. Найти РК, если ВС=8м.
20. Параллельные плоскости a и b пересекают сторону АВ угла ВАС соответственно в точках А1 и А2, и сторону АС этого угла - соответственно в точках В1 и В2. Найти А2В2 и АА2, если А1В1=18см., АА1=24см., АА2=3/2А1А2. 12. Через точку К проведены две прямые a и b, пересекающие две параллельные плоскости a и b: первую в точках А1 и А2, вторую в точках В1 и В2 соответственно. Вычислить КА1 и КВ2, если:
а) А1А2/В1В2=3/4, А1В1=7дм, КА2=12дм;
б) А1А2/ В1В2=1/6, А2В2=3см, В1К=12см.
Точка К не лежит между плоскостями a и b.
13.В треугольнике АВС АВ=15м., АС=24м. Через точку М на стороне АВ, находящейся на расстоянии 10м от точки А, проведена плоскость, параллельная прямой АС и пересекающая сторону ВС в точке К. Найдите длину отрезка МК.
14. Плоскость, параллельная стороне АВ треугольника АВС, пересекает его стороны в точках М и К. Найти АВ, если М- середина стороны АС и МК=10мм.
15. Параллельные плоскости a и b пересекают стороны угла АВС в точках А1, С1, А2, С2 соответственно. Найти ВС1, если А1В/А1А2=1/3, ВС2=12мм.
16. Точка К лежит между параллельными плоскостями a и b. Прямые а и b, проходящие через точку К, пересекают плоскость a в точках А1 и В1, а плоскость b в точках А2 и В2 соответственно. Найти КВ1, если:
а) А1К/А1А2=1/3, В1В2=15м.;
б) В1А1/В2А2=4/6, КВ2=8дм;
в) А2К/А1А2=2/5, В1В2=20см;
г) КВ2/А1В1=1/6, А2В2=2мм.
17. Треугольник АРD и трапеция АВСD имеют общую сторону АD и лежат в разных плоскостях. Через основание ВС трапеции и середину отрезка РD – точку К проведена плоскость, которая пересекает прямую АР в точке М. Найти МК, если АД=10м.
18. Через точку А стороны КМ треугольника КМР проведена плоскость, параллельная прямой МР. Вычислить длину отрезков, на которые делится эта плоскость сторону КР, если МК=10см., МА=6см, КР=15дм.
19. Треугольники АВС и DВС не лежат в одной плоскости и имеют общую сторону; точки М, Н, К- середины соответственно сторон ВD, DС, АС. Отрезок АВ пересекает плоскость МКН в точке Р. Найти РК, если ВС=8м.
20. Параллельные плоскости a и b пересекают сторону АВ угла ВАС соответственно в точках А1 и А2, и сторону АС этого угла - соответственно в точках В1 и В2. Найти А2В2 и АА2, если А1В1=18см., АА1=24см., АА2=3/2А1А2.
|
|
ДОПОЛНИТЕЛЬНЫЕ ЗАДАНИЯ. | |||||||
|
1. Продолжение отрезка ВС пересекает плоскость
|
| ||||||
| 2. На рисунке изображены параллельные плоскости | |||||||
|
|
Скопируйте рисунок и изобразите на нём точку В, принадлежащую плоскости | ||||||
| 3. Зарисуйте примеры конструкций, которые спереди и слева имеют следующий вид. (В конструкции используйте только кубики).
4. На рисунке изображены геометрические тела, на поверхности которых отмечены точки. Назовите эти фигуры, нарисуйте развёртки поверхностей этих тел и покажите на них соответствующие точки. Примеры развёрток смотрите в приложении.
| |||||||
| 5. Постройте развёртку поверхности куба: а) ребро которого равно 35мм; б) диагональ грани которого равна 4см. Склейте эти модели ( припуски удобней делать на боковых гранях). 6. Рассмотрите набор деревянных брусков. Выясните можно ли составить каждый брусок из кубиков с ребром а= 2 клетки? Если да, то сколько кубиков понадобится для работы?
7. Перерисуйте из приложения развертку: правильной треугольной призмы; правильной пятиугольной призмы; наклонного параллелепипеда. Обозначьте вершины у каждой фигуры и перечислите: а) все параллельные ребра (нарисуйте их одним цветом); б) все диагонали боковых граней и оснований (нарисуйте их другим цветом); | |||||||
| в) все диагонали призмы и параллелепипеда. Для выполнения этого задания развёртки фигур необходимо увеличить и склеить (припуски удобней делать на боковых гранях).
8. Сколько прямоугольных параллелепипедов изображено на рисунке?
9. Туго натянутая нить последовательно закреплена в точках | |||||||
|
| 1, 2, 3, 4, 5 и 6, расположенных на стержнях SA, SB и SC, которые не принадлежат одной плоскости. Скопируйте рисунок, отметьте и обозначьте точки, в которых отрезки нити соприкасаются | ||||||
| 10. Туго натянутая нить последовательно закреплена в точках | |||||||
|
| 1, 2, 3, 4, и 5, расположенных на стержнях SA, SB и SC, которые не принадлежат одной плоскости. Скопируйте рисунок, отметьте и обозначьте точки, в которых отрезки нити соприкасаются. | ||||||
|
ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ | |||||||
|
ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ Две прямые называются перпендикулярными, если они пересекаются под прямым углом. | |||||||
|
ПЕРПЕНДИКУЛЯР И НАКЛОННЫЕ | |||||||
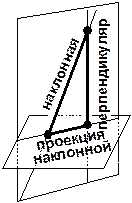 Перпендикуляр короче любой наклонной, проведенной к плоскости из той же точки.
Перпендикуляр короче любой наклонной, проведенной к плоскости из той же точки.
|
У равных наклонных, проведенной к плоскости из одной точки, проекции равны. Справедливо и обратное: если у двух наклонных, проведенных из одной точки, проекции равны, то равны и наклонные. |  Из двух наклонных, проведенных из одной точки, больше та, у которой проекция больше.
Справедливо и обратное.
Из двух наклонных, проведенных из одной точки, больше та, у которой проекция больше.
Справедливо и обратное.
| |||||
|
Теорема о трёх Перпендикулярах. (содержит два утверждения: прямое и обратное) Если прямая, лежащая в плоскости и проходящая через основание наклонной, перпендикулярна проекции наклонной, то она перпендикулярна и самой наклонной. Если прямая, лежащая в плоскости и проходящая через основание наклонной, перпендикулярна наклонной, то она перпендикулярна и проекции наклонной. | |||||||
|
СКРЕЩИВАЮЩИЕСЯ ПРЯМЫЕ Так называются прямые, которые не лежат в одной плоскости, то есть не параллельны и не пересекаются. | |
|
Углы в пространстве | |
|
Двугранный угол | |
| Так называется фигура, образованная двумя полуплоскостями с общей ограничивающей их прямой (эта прямая называется ребром двугранного угла). |
|
Угол между плоскостями | |

| Две пересекающиеся плоскости определяют четыре двугранных угла. Сумма двух таких углов, имеющих общую грань, равна 1800. Углом между плоскостями называют меньший из этих углов:
00 < j 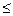 900. (Если j =900, плоскости перпендикулярны.) 900. (Если j =900, плоскости перпендикулярны.)
|
|
УПРАЖНЕНИЯ | ||
| 1. ABCDA 1 B 1 C 1 D 1 – куб. | ||
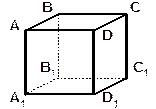
| 1. Выпишите: а) ребра, перпендикулярные плоскостям АВС, DCC1, ABB1; б) плоскости, перпендикулярные ребру ВС, ВВ1, А1D1. 2. Используя символы ^ и ||, запишите: а) как расположены прямые DD1 и CC1, АА1 и А1В1, DC и ВС; | |
| б) как расположены прямая и плоскость СС1 и DCB, АА1 и DCD1, D1C1 и DCB, В1С1 и DCB. 2. Как расположены прямая a и b, если: а) прямые a,b и с лежат в плоскости a, прямая m ^ a, m ^ b, но m не перпендикулярна с; б) прямая a ^ a, b || a, a и b лежат в плоскости b; в) прямая a || a, b ^ a, но прямая b не пересекает прямую a. 3. Как расположены прямые b и с, если: а) прямые a, b и c лежат в плоскости a, m ^ c, m ^ b, но m не перпендикулярна a; б) прямые b и с лежат в плоскости a, a ^ b, a ^ с, но прямая а не перпендикулярна a. 4. Прямая а ^ a, прямая b || a, причем a и b лежат в плоскости b. Как расположены плоскости a и b. 5. Плоскости a и b перпендикулярны, a 6. SABCD – правильная пирамида (ABCD – квадрат, O – центр). | ||
|
| Выпишите: а) расстояние от точки S до плоскости АВСD; б) проекции всех ребер на плоскость основания АВСD; в) расстояние от точки S до сторон основания ABCD и их проекции. | |
| 7. SABC – правильная пирамида ( Укажите, как обозначено: а) расстояние от точки S до плоскости АВС; б) проекции всех рёбер на плоскость основания ABCD; в) расстояние от точки S до сторон основания и их проекции. |
| ||||
| 8. Из точки А, данной на расстоянии 12 см, проведена наклонная. Найдите: а) длину наклонной, если её проекция равна 5 см; б) определите проекцию наклонной, если наклонная равна 20 см. |
| ||||
| 9. Под каким углом к плоскости надо провести наклонную, чтобы: а) перпендикуляр был в два раза меньше наклонной; б) проекция и длина перпендикуляра были равны. 10. Из одной точки к плоскости проведены две наклонные. Одна имеет проекцию 2 м, а другая 3 м. Какая из наклонных образует с плоскостью меньший угол. | |||||
| 11. Через вершину острого угла прямоугольного треугольника АВС с прямым углом С проведена прямая АD. АD перпендикулярна плоскости треугольника. Чему равно расстояние от точки D до вершины С, если АС = 6см., АD = 8 см.? | 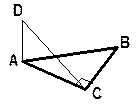
| ||||
| 12. Отрезок АВ длиной 10 дм своими концами упирается в две параллельные плоскости a и b, расстояние между которыми равно 8 дм. Найдите проекции отрезка на эти плоскости. | 
| ||||
|
13.
|
Из точки М, отстоящей от плоскости на расстоянии 6 см, проведены к этой плоскости наклонные МА и МВ, образующие с ней углы 450 и 300, а между собой прямой угол. Найдите расстояние между основаниями наклонных. | ||||
|
14.
|
На изображении прямоугольного параллелепипеда ABCDA1B1C1D1 укажите общий перпендикуляр прямых: AD и СС1, A1B1 и CB, АВ и DD1, СВ и АА1. Укажите длину каждого найденного перпендикуляра, если длины сторон основания А1В1=10см, D1A1=8см, а высота параллелепипеда АА1=6 см. | ||||
|
15.
|
Ребро куба ABCDA1B1C1D1 равно а. Найдите расстояние d между прямыми: 1) АВ и СС1; 2) СС1 и В1D1; 3) АС и В1D1; 4) СС1 и ВD1. | ||||
| 16. На изображении куба ABCDA1B1C1D1 постройте общий перпендикуляр прямых: СС1 и D1B1, DB и А1С1. Найдите расстояние между этими прямыми, если ребро куба равно b. 17. Докажите, что все прямые, проходящие через данную точку М прямой а и перпендикулярные к этой прямой, лежат в плоскости, проходящей через точку М и перпендикулярной к прямой а. 18. Луч ВА не лежит в плоскости неразвёрнутого угла СВD. Докажите, что если ÐАВС = ÐАВD, причём ÐАВС<900, то проекцией луча ВА на плоскость СВD является биссектриса угла СВD. | |||||
| 19. Даны два двугранных угла, у которых одна грань общая, а две другие грани являются различными полуплоскостями одной плоскости. Докажите, что сумма этих двугранных углов равна 1800. 20. Плоскости плоскости 21. Плоскости
| |||||
|
ПРОЧИТАЙТЕ УСЛОВИЕ ЗАДАЧ И РАЗБЕРИТЕ ИХ РЕШЕНИЕ | |||||
|
ДОПОЛНИТЕЛЬНЫЕ ЗАДАНИЯ | |||||
| 1. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение: а) плоскостью АВС1; б) плоскостью АСС1. Докажите, что построенные сечения являются параллелограммами. 2. Точка S равноудалена от вершин прямоугольного треугольника и не лежит в плоскости этого треугольника. Докажите, что прямая SM где М – середина гипотенузы, перпендикулярна к плоскости треугольника. | |||||
| 3. Точка М – середина ребра AD куба, изображённого на рисунке. Скопируйте рисунок и изобразите точку N, принадлежащую ребру CD, так, чтобы отрезки А1N и С1М имели общую точку. | 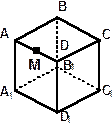
| ||||
| 4. Можно ли из данных плоских фигур получить модели геометрических тел? Если можно, то какие и как это сделать?
| |
| 6. Точки K, L, M и N принадлежат рёбрам изображённой на рисунке пирамиды. Скопируйте рисунок и определите, пересекаются ли прямые KL и MN, отрезки KN и LM. | 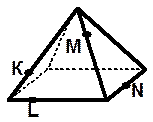
|
| 7. Решите анаграммы и исключите лишнее слово: а) лоннанаяк ; пенлярперкуди; ципрояек; ачток; б) давктар; кинтрельуго; гурк; бук; в) стькоспло; паямяр; ачток; тояраснисе; г) чул; аямпря; козрето; луго.
8. Постройте развёртку поверхности правильной пирамиды, боковое ребро которого равно 5,5см., а основание является: а) равносторонним треугольником со стороной 4,3см; б) квадратом с диагональю 5см; в) ромбом со стороной 4см. и одним из углов, равным 850; г) правильный шестиугольник со стороной 3см. 9. Сколько пирамид изображено на рисунке? Разделение пирамид ведите по линиям.
10. Перерисуйте из приложения (в конце пособия) развёртки треугольной пирамиды и правильной четырёхугольной пирамиды. Склейте из этих развёрток пирамиды и обозначьте разными цветами: а) расстояние от вершины пирамиды до вершин основания; б) расстояние от вершины пирамиды до плоскости основания; в) радиусы вписанной и описанной окружности основания правильной четырёхугольной пирамиды; г) линейный угол между боковой гранью и основанием.
11. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей через диагональ АС основания параллельно диагонали ВD1. Докажите, что если основание параллелепипеда – ромб и углы АВВ1 и СВВ1 прямые, то построенное сечение – равнобедренный треугольник
| |
| 3 МНОГОГРАННИКИ Так называются тела, поверхность которых состоит из конечного числа плоских многоугольников. Многогранник называют выпуклым, если он весь лежит по одну сторону от плоскости любой его грани; тогда грани его тоже выпуклы. |
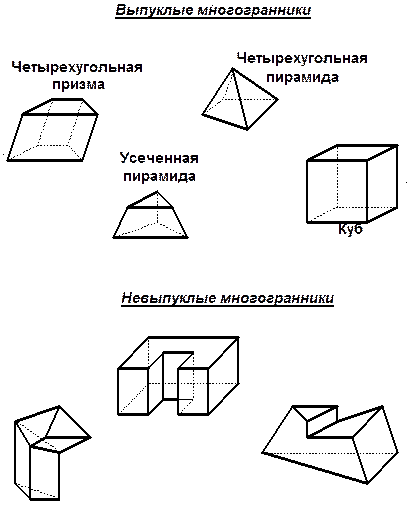
|
|
ПРИЗМА Так называется многогранник, две грани которого (основания) – равные n – угольники, лежащие в параллельных плоскостях, а остальные n- граней (боковые грани) – параллелограммы. | |
|
ОСНОВНЫЕ ЭЛЕМЕНТЫ ПРИЗМЫ | |
|
Высота призмы – перпендикуляр, проведенный из точки одного основания к плоскости другого. Диагональ призмы – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани. Диагональное сечение – сечение, которое проходит через какую-нибудь диагональ призмы и боковое ребро. Поверхность призмы состоит из двух оснований и боковой поверхности. Боковая поверхность состоит из параллелограммов. | |
|
ОСНОВНЫЕ ВИДЫ ПРИЗМ | |
|
| |
| ПАРАЛЛЕЛЕПИПЕД Так называется призма, основания которой параллелограммы. | |
| СВОЙСТВА ПАРАЛЛЕЛЕПИПЕДА Противолежащие грани равны и параллельны. Все четыре диагонали пересекаются в одной точке и точкой пересечения делятся пополам. Точка пересечения диагоналей – центр симметрии. | |
| ВИДЫ ПАРАЛЛЕЛЕПИПЕДОВ | |

| |
|
ПИРАМИДА Так называется многогранник, одна грань которого (основание) – многоугольник, а все остальные грани (боковые) - треугольники, имеющие общую вершину (вершина пирамиды). | |
|
ОСНОВНЫЕ ЭЛЕМЕНТЫ ПИРАМИДЫ | |
|
Высота пирамиды – перпендикуляр, опущенный из вершины пирамиды на плоскость основания. Диагональное сечение – сечение, проходящее через два не соседних боковых ребра пирамиды. Поверхность пирамиды состоит из основания и боковых граней. Каждая боковая грань – треугольник. | |
|
ОСНОВНЫЕ ВИДЫ ПИРАМИД | |
|
| |

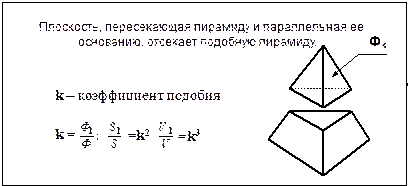
| |
| ПРАВИЛЬНЫЙ МНОГОГРАННИК Так называется многогранник, у которого: - все грани – равные правильные многоугольники; - все многогранные углы имеют одинаковое число граней; - все ребра – равные отрезки; - все плоские углы – равные углы. | |
| ВИДЫ ПРАВИЛЬНЫХ МНОГОГРАННИКОВ |
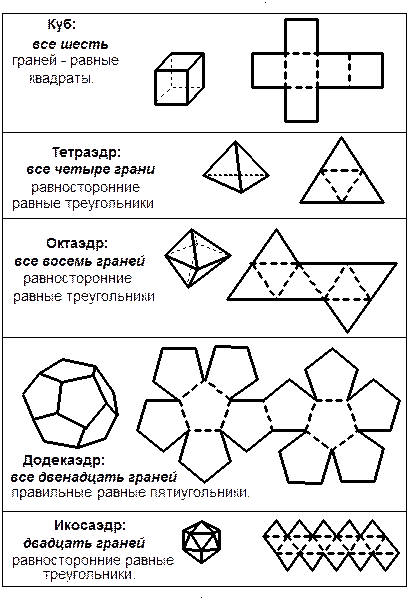
|
|
УПРАЖНЕНИЯ | |
| 1. Какие из фигур, изображенных на рисунке, являются призмами и почему?
2. Существует ли треугольная призма, у которой: а) только две боковые грани - прямоугольники; б) только две боковые грани перпендикулярны плоскости основания; в) только одна боковая грань – прямоугольник? 3. ABCDEFKA 1 B 1 C 1 D 1 E 1 F 1 K 1 - невыпуклая прямая призма. | |
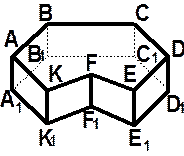
| Выпишите: а) основания; б) параллельные боковые грани; в) все грани, проходящие через точку С; г) все грани параллельные ребру КК1 (см. тему " Параллельные прямая и плоскость"); д) все диагонали призмы. |
| 4. Верно ли утверждение: а) основанием наклонной призмы является правильный многоугольник; б) куб является призмой; в) если призма наклонная, то ее высота равна длине бокового ребра; г) высота призмы – отрезок, соединяющий две вершины, не лежащие в одной грани; д) если сторона основания правильной четырехугольной призмы равна ее высоте, то эта призма куб? 5. Сделайте рисунок наклонной четырехугольной призмы, обозначьте ее и запишите: вершины, основания, боковые ребра, боковые грани, противоположные грани. 6. Среди изображенных тел выберите номера тех, которые являются параллелепипедом.
7. Какое из утверждений является неверным: а) призма – это многогранник; б) параллелепипед – это многоугольник; в) усечённая пирамида - пирамида? 8. Из скольких кубиков с ребром 3 см каждый можно составить куб с ребром 15 см?
| |
| 9. В кубе из одной вершины проведены две диагонали боковых граней. Чему равен угол между ними? | 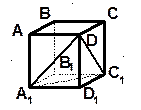
|
| 10. Верно ли утверждение: а) прямоугольник может быть основанием наклонного параллелепипеда; б) наклонный параллелепипед имеет множество плоскостей симметрии; в) параллелепипед имеет четыре диагонали; г) существует такой наклонный параллелепипед, у которого четыре грани прямоугольники?
| |||||||
| 11. Вершинами некоторого многогранника являются центр верхней грани куба, и середины всех сторон нижней его грани. Как называется этот многогранник? Перечислите равные ребра, и укажите какие грани этого многогранника равны между собой. | 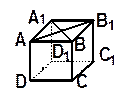
| ||||||
|
12. Ответьте на вопросы а) сколько боковых ребер пирамиды могут быть перпендикулярными к плоскости основания; б) будет ли пирамида правильной, если ее боковыми гранями являются правильные треугольники? 13. Верно ли утверждение: а) пирамида всегда будет правильной, если в ее основании лежит правильный многоугольник; б) высота боковой грани правильной пирамиды – апофема; в) в любой пирамиде можно провести апофему; г) тетраэдр – правильный многогранник; д) наименьшее число ребер, какое может иметь пирамида – шесть; е) тетраэдр имеет несколько плоскостей симметрии, проходящих через данную вершину. 14. В правильной треугольной пирамиде SABC: а) укажите угол между боковой гранью SAB и плоскостью основания АВС, для этого постройте линейный угол этих плоскостей; б) укажите радиус вписанной и описанной окружности основания; | |||||||
| в) вычислите r и R, если АВ=10 см; г) вычислите длину бокового ребра и высоту, если боковое ребро наклонено к плоскости основания под углом 600. 15. Известно, что многогранник, у которого 26 вершин, является призмой. Какой многоугольник лежит в основании этой призмы? Сколько боковых граней имеет эта призма? 16. Может ли пирамида иметь: а) 13 рёбер; б) 14 рёбер; в)13 боковых рёбер? Если такая пирамида существует, то какая она? 17. Может ли призма иметь: а) 15 рёбер; б) 28 рёбер; в) 8 боковых рёбер? Если эта призма существует, то какая она? Сколько у неё боковых рёбер, вершин? | |||||||
|
ПРОЧИТАЙТЕ УСЛОВИЕ ЗАДАЧ И РАЗБЕРИТЕ ИХ РЕШЕНИЕ
В правильной четырехугольной призме со стороной основания 6 дм и высотой 15 дм проведено диагональное сечение, которое разбивает ее на две треугольные призмы. Найдите площадь боковых поверхностей треугольных призм. | |||||||
| Дано: АВСDА1В1С1D1 – правильная призма. АВ=6 дм. h =АА1 =15дм АВВ1А1 – диагональное сечение; Найти: Sбок. АВСА1В1 С1. |
| Решение: 1) АВСDА1В1С1D1 - правильная призма, значит, диагональное сечение АСС1А1 дели ее на две равные треугольные призмы, | |||||
| тогда боковые грани – равные прямоугольники АВВ1А1 = ВСС1В1 = СDD1C1 =АDD1А1. Sбок. АВСА1В1 С1=2 SАВВ1А1+ SАСС1А1. SАВВ1А1 =АВ · АА1 = 6·15 = 90 (дм2). 2) SАСС1А1 -? АСС1А1 – прямоугольник, SАСС1А1 = АС·СС1, СС1 =15 дм, АС -? 3) Найдем АС, для этого рассмотрим прямоугольный Sбок. АВСА1В1 С1 = 2 ·90 + 90 Ответ: Sбок. АВСА1В1 С1 = 90( 2 + 4. Дан прямоугольный параллелепипед KLMNK 1 L 1 M 1 N 1 , сторона KL = 7м, а LM = 24 м. Диагональ параллелепипеда наклонена к плоскости основания под углом 450. Найдите высоту параллелепипеда. | |||||||
| Дано: KLMNK1L1M1N1 – прямоугольный параллелепипед. KL =7м. LM = 24м.
Найти: KK1 |
| Решение: 1) Рассмотрим 2) Найдем KM из прямоугольного | |||||
| т. Пифагора KM2 = KL2 + LM2 = 72 + 242 = 49 + 586 = 625, KM = Ответ: KK1 = 25 дм. Дано: FKLV – правильная пирамида. а = KL = 12 м l = FN= 8 м. Найти: FK, FО. |
| Решение: 1) Боковое ребро FK найдем из прямоугольного | |||||||||
| ( NK = KL : 2 т.к. FN – высота и медиана 2) FО -? Из прямоугольного | |||||||||||
| 3) NO - ? NO = r – радиус вписанной окружности в NO = Тогда FO2 = 82 – (2 Ответ: FK = 10м, FO =2 В основании пирамиды лежит прямоугольный треугольник, гипотенуза которого равна 15 дм, а один из катетов – 9 дм. Найдите площадь сечения, проведенного через середину высоты пирамиды, параллельно ее основанию. | |||||||||||
| Дано: SABC – пирамида.
АС = 15 дм, ВС =9 дм.
Найти: S |
| Решение:
1) Сечения АВС и А1В1С1 – подобны с коэффициентом подобия k = 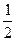 , известно, что , известно, что
| |||||||||
|
2) S АВ = Ответ: S
| |||||||||||
| РИСУНКИ К ЗАДАЧАМ (призма) |
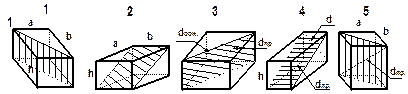

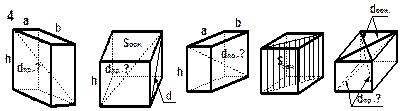
 Примечание: а, b -стороны основания; h -высота;
S осн. -площадь основания;
S сеч. -площадь сечения;
d пр.(осн.) -диагональ призмы (основания).
Примечание: а, b -стороны основания; h -высота;
S осн. -площадь основания;
S сеч. -площадь сечения;
d пр.(осн.) -диагональ призмы (основания).
|
| РИСУНКИ К ЗАДАЧАМ (пирамида) |
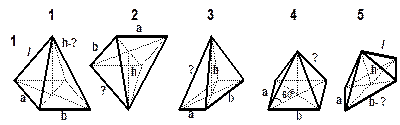
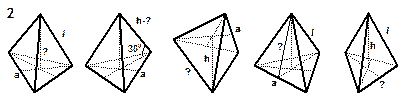
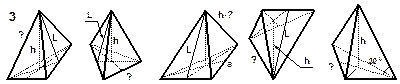
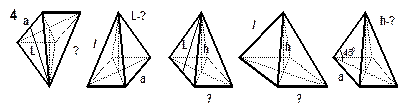
 Примечание: а, b, с – стороны основания;
h – высота;
L – апофема;
l – длина бокового ребра;
S сеч. – площадь сечения. Примечание: а, b, с – стороны основания;
h – высота;
L – апофема;
l – длина бокового ребра;
S сеч. – площадь сечения.
|
| 3.2 ЗАДАЧИ (призма) |
1. Дана прямая призма, в основании которой лежит прямоугольник. Диагональ призмы 15м. Высота призмы равна 7м. Найдите площадь диагонального сечения.
2. В правильной треугольной призме АВСА1В1С1 проведено сечение через вершину С1 и ребро АВ. найдите периметр сечения, если сторона основания равна 24см., а боковое ребро- 10см.
3. Диагональное сечение правильной четырёхугольной призмы, у которой сторона основания равна 10см. и высота 12см., разбивает её на две треугольные призмы. Найдите площади боковых поверхностей треугольных призм.
4. В правильной четырёхугольной призме площадь основания равна 144дм2, а высота 14дм. Найдите диагональ призмы.
5. Определите диагональ прямоугольного параллелепипеда по трём его измерениям 1, 2, 2.
6. Стороны основания прямоугольного параллелепипеда равны 9м. и 12м., а диагональ наклонена к плоскости основания под углом 450. Найдите высоту параллелепипеда.
7. Высота прямой призмы равна 10см. Основанием призмы является прямоугольник со сторонами 6см. и 8см. Найдите площадь диагонального сечения.
8. В правильной четырёхугольной призме диагональ боковой грани 23м., а диагональ основания 20м. Найдите диагональ призмы.
9.Длины рёбер прямоугольного параллелепипеда равны 6см.. 8см. и 24см. Найдите длины его диагоналей.
10. В основании прямой призмы лежит прямоугольник со сторонами 2м. и 2  м. Диагональ призмы наклонена к плоскости основания под углом 450. Найдите длину бокового ребра.
11. В прямой призме основанием является прямоугольник со сторонами 2м. и 4м. Высота этой призме равна 3м. Найдите площадь диагонального сечения.
12.АВСА1В1С1- прямая треугольная призма, в основании которой лежит равнобедренный треугольник со сторонами 10см., 10см. и 13см. Найдите площадь сечения, проходящего через вершину В и ребро А1С1, если высота призмы равна 2см. м. Диагональ призмы наклонена к плоскости основания под углом 450. Найдите длину бокового ребра.
11. В прямой призме основанием является прямоугольник со сторонами 2м. и 4м. Высота этой призме равна 3м. Найдите площадь диагонального сечения.
12.АВСА1В1С1- прямая треугольная призма, в основании которой лежит равнобедренный треугольник со сторонами 10см., 10см. и 13см. Найдите площадь сечения, проходящего через вершину В и ребро А1С1, если высота призмы равна 2см.
|
13. В правильной четырёхугольной призме диагональ боковой грани 10м., а диагональ основания 8  м. Найдите площадь диагонального сечения.
14 Найдите диагональ прямоугольного параллелепипеда, если диагонали его граней имеют длины 11, 19 и 20м.
15. В прямоугольном параллелепипеде стороны основания равны 5см. и 12см., а диагональ параллелепипеда наклонена к плоскости основания под углом 450. Найдите высоту параллелепипеда.
16. Основанием прямой призмы служит прямоугольник. Диагональ основания равна 6дм., а диагональ призмы 8дм. Найдите площадь диагонального сечения.
17. Сторона основания правильной треугольной призмы равна 24м, а высота призмы 18см. Найдите периметр сечения, проведённого через сторону нижнего основания и противолежащую вершину верхнего основания.
18. Определите диагонали прямоугольного параллелепипеда по трём его измерениям 2, 3, 6.
19. Стороны прямоугольника, который лежит в основании прямой призмы, равны 4см и 6см. Высота-8см. Найдите площадь диагонального сечения.
20. Найдите высоту правильной четырёхугольной призмы, если сторона основания равна 2м, а диагональ составляет с плоскостью основания угол 450.
21. В правильной треугольной призме сторона основания равна 12м., а высота – 9м. Найдите периметр сечения, проходящего через вершину С и ребро А1В1.
22. Сторона основания правильной четырёхугольной призмы равна 4м, а высота- 8м. Найдите площади боковых поверхностей треугольной призмы, образованной диагональным сечением.
23. В основании прямоугольного параллелепипеда лежит квадрат со стороной 4см. Диагональ параллелепипеда образует с плоскостью основания угол 600. Найдите высоту призмы.
24. В правильной треугольной призме сторона основания равна 8см., а высота 6см. Найдите площадь сечения, проведенного через ребро А1С1 и вершину В. м. Найдите площадь диагонального сечения.
14 Найдите диагональ прямоугольного параллелепипеда, если диагонали его граней имеют длины 11, 19 и 20м.
15. В прямоугольном параллелепипеде стороны основания равны 5см. и 12см., а диагональ параллелепипеда наклонена к плоскости основания под углом 450. Найдите высоту параллелепипеда.
16. Основанием прямой призмы служит прямоугольник. Диагональ основания равна 6дм., а диагональ призмы 8дм. Найдите площадь диагонального сечения.
17. Сторона основания правильной треугольной призмы равна 24м, а высота призмы 18см. Найдите периметр сечения, проведённого через сторону нижнего основания и противолежащую вершину верхнего основания.
18. Определите диагонали прямоугольного параллелепипеда по трём его измерениям 2, 3, 6.
19. Стороны прямоугольника, который лежит в основании прямой призмы, равны 4см и 6см. Высота-8см. Найдите площадь диагонального сечения.
20. Найдите высоту правильной четырёхугольной призмы, если сторона основания равна 2м, а диагональ составляет с плоскостью основания угол 450.
21. В правильной треугольной призме сторона основания равна 12м., а высота – 9м. Найдите периметр сечения, проходящего через вершину С и ребро А1В1.
22. Сторона основания правильной четырёхугольной призмы равна 4м, а высота- 8м. Найдите площади боковых поверхностей треугольной призмы, образованной диагональным сечением.
23. В основании прямоугольного параллелепипеда лежит квадрат со стороной 4см. Диагональ параллелепипеда образует с плоскостью основания угол 600. Найдите высоту призмы.
24. В правильной треугольной призме сторона основания равна 8см., а высота 6см. Найдите площадь сечения, проведенного через ребро А1С1 и вершину В.
|
 25. Площадь основания правильной четырёхугольной призмы равна 81дм2, а высота-5дм. Найдите площади боковых поверхностей треугольных призм, образованных диагональным сечением.
26. В правильной четырёхугольной призме расстояние от вершины верхнего основания до середины диагонали нижнего основания равно 10см. Высота призмы 6см. Найдите длины сторон оснований призмы.
27. В правильной четырёхугольной призме ABCDA1B1C1D1 площадь основания равна 16см2. Найдите расстояние между прямыми АА1 и В1D.
28.В правильной треугольной призме боковое ребро равно 3см., а расстояние от вершины верхнего основания до середины противоположной стороны нижнего основания равно 6см. Найдите длины остальных рёбер призмы. 25. Площадь основания правильной четырёхугольной призмы равна 81дм2, а высота-5дм. Найдите площади боковых поверхностей треугольных призм, образованных диагональным сечением.
26. В правильной четырёхугольной призме расстояние от вершины верхнего основания до середины диагонали нижнего основания равно 10см. Высота призмы 6см. Найдите длины сторон оснований призмы.
27. В правильной четырёхугольной призме ABCDA1B1C1D1 площадь основания равна 16см2. Найдите расстояние между прямыми АА1 и В1D.
28.В правильной треугольной призме боковое ребро равно 3см., а расстояние от вершины верхнего основания до середины противоположной стороны нижнего основания равно 6см. Найдите длины остальных рёбер призмы.
|
| ЗАДАЧИ (пирамида) |
1. В правильной треугольной пирамиде сторона основания равна 12 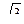 см., а каждое боковое ребро 13см. Найдите высоту пирамиды.
2. В основании пирамиды лежит прямоугольник со сторонами 3м. и 3 см., а каждое боковое ребро 13см. Найдите высоту пирамиды.
2. В основании пирамиды лежит прямоугольник со сторонами 3м. и 3 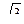 м. Высота пирамиды равна 4м. Найдите длину бокового ребра.
3. Найдите сторону основания правильной треугольной пирамиды, если высота пирамиды равна 6м., а апофема 10м.
4. В правильной четырёхугольной пирамиде сторона основания равна 12мм., а апофема 8мм. Найдите боковое ребро пирамиды.
5. В основании пирамиды лежит прямоугольник, гипотенуза которого равна 13м., а один из катетов-12м. Найдите площадь сечения, проведённого через середину высоты пирамиды, параллельно её основанию.
6. Каждая боковая грань правильной треугольной пирамиды наклонена к плоскости основания под углом 300. Найдите сторону основания, если высота пирамиды равна 10мм.
7. Найдите сторону основания правильной треугольной пирамиды, если известно, что высота пирамиды равна 21м., а длина бокового ребра-29м. м. Высота пирамиды равна 4м. Найдите длину бокового ребра.
3. Найдите сторону основания правильной треугольной пирамиды, если высота пирамиды равна 6м., а апофема 10м.
4. В правильной четырёхугольной пирамиде сторона основания равна 12мм., а апофема 8мм. Найдите боковое ребро пирамиды.
5. В основании пирамиды лежит прямоугольник, гипотенуза которого равна 13м., а один из катетов-12м. Найдите площадь сечения, проведённого через середину высоты пирамиды, параллельно её основанию.
6. Каждая боковая грань правильной треугольной пирамиды наклонена к плоскости основания под углом 300. Найдите сторону основания, если высота пирамиды равна 10мм.
7. Найдите сторону основания правильной треугольной пирамиды, если известно, что высота пирамиды равна 21м., а длина бокового ребра-29м.
|
8. Дана четырёхугольная пирамида в основании которой лежит прямоугольник со сторонами 6дм. и 2 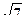 дм. Каждое боковое ребро наклонено к плоскости основания под углом 600. Найдите длину бокового ребра.
9. Найдите апофему правильной треугольной пирамиды, если сторона основания равна 4 дм. Каждое боковое ребро наклонено к плоскости основания под углом 600. Найдите длину бокового ребра.
9. Найдите апофему правильной треугольной пирамиды, если сторона основания равна 4 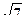 см., а длина каждого бокового ребра 6см.
10. Стороны оснований правильной усечённой треугольной пирамиды 4дм. и 1дм. Боковое ребро 2дм. Найдите высоту пирамиды.
11. Апофема правильной треугольной пирамиды равна 6дм., а сторона основания 6 см., а длина каждого бокового ребра 6см.
10. Стороны оснований правильной усечённой треугольной пирамиды 4дм. и 1дм. Боковое ребро 2дм. Найдите высоту пирамиды.
11. Апофема правильной треугольной пирамиды равна 6дм., а сторона основания 6 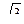 дм. Найдите высоту пирамиды.
12. Сторона основания правильной четырёхугольной пирамиды равна 4 дм. Найдите высоту пирамиды.
12. Сторона основания правильной четырёхугольной пирамиды равна 4 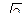 м. Найдите апофему данной пирамиды, если длина бокового ребра равна 5м.
13. Основание пирамиды- прямоугольник со сторонами 6см. и 8см. Каждое боковое ребро пирамиды равно 10см. Найдите высоту пирамиды.
14. В правильной треугольной пирамиде боковые ребра наклонены к плоскости основания под углом 300. Сторона основания равна 12м. Найдите высоту пирамиды.
15. Высота правильной треугольной пирамиды равна 12см., а апофема 13см. Найдите длину бокового ребра пирамиды.
16. Высота правильной четырёхугольной усечённой пирамиды равна 4дм. Стороны оснований-2дм. и 8дм. Найдите площади диагональных сечений.
17. Найдите сторону основания правильной четырёхугольной пирамиды, если высота пирамиды равна 2 м. Найдите апофему данной пирамиды, если длина бокового ребра равна 5м.
13. Основание пирамиды- прямоугольник со сторонами 6см. и 8см. Каждое боковое ребро пирамиды равно 10см. Найдите высоту пирамиды.
14. В правильной треугольной пирамиде боковые ребра наклонены к плоскости основания под углом 300. Сторона основания равна 12м. Найдите высоту пирамиды.
15. Высота правильной треугольной пирамиды равна 12см., а апофема 13см. Найдите длину бокового ребра пирамиды.
16. Высота правильной четырёхугольной усечённой пирамиды равна 4дм. Стороны оснований-2дм. и 8дм. Найдите площади диагональных сечений.
17. Найдите сторону основания правильной четырёхугольной пирамиды, если высота пирамиды равна 2 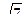 м., а апофема 8м.
18. Боковое ребро пирамиды разделено на четыре равные части и через точки деления проведены плоскости, параллельные основанию. Площадь основания равна 400см2. Найдите площади сечений.
19. Основание пирамиды – прямоугольник со сторонами 8см. и 6см. Высота пирамиды равна 12см. Найдите длину бокового ребра. м., а апофема 8м.
18. Боковое ребро пирамиды разделено на четыре равные части и через точки деления проведены плоскости, параллельные основанию. Площадь основания равна 400см2. Найдите площади сечений.
19. Основание пирамиды – прямоугольник со сторонами 8см. и 6см. Высота пирамиды равна 12см. Найдите длину бокового ребра.
|
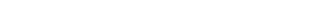 20. В правильной треугольной пирамиде сторона основания равна 3 20. В правильной треугольной пирамиде сторона основания равна 3  м. Высота пирамиды равна 4м. Найдите длину бокового ребра.
21. В основании пирамиды лежит прямоугольный треугольник, гипотенуза которого равна 25м., а катет 7м. Найдите площадь сечения, проведенного через середину высоты пирамиды параллельно её основанию.
22. Найдите сторону основания правильной четырёхугольной пирамиды, если боковое ребро равно 6м., а высота 2м.
23. Найдите длину бокового ребра правильной треугольной пирамиды, если апофема пирамиды равна 41мм., а высота 40мм.
24. Найдите высоту правильной четырёхугольной пирамиды, если сторона основания равна 7 м. Высота пирамиды равна 4м. Найдите длину бокового ребра.
21. В основании пирамиды лежит прямоугольный треугольник, гипотенуза которого равна 25м., а катет 7м. Найдите площадь сечения, проведенного через середину высоты пирамиды параллельно её основанию.
22. Найдите сторону основания правильной четырёхугольной пирамиды, если боковое ребро равно 6м., а высота 2м.
23. Найдите длину бокового ребра правильной треугольной пирамиды, если апофема пирамиды равна 41мм., а высота 40мм.
24. Найдите высоту правильной четырёхугольной пирамиды, если сторона основания равна 7  м., а каждое боковое ребро наклонено к плоскости основания под углом 450.
25. Дана пирамида KLMNF, основание LMNF- прямоугольник со сторонами 2 м., а каждое боковое ребро наклонено к плоскости основания под углом 450.
25. Дана пирамида KLMNF, основание LMNF- прямоугольник со сторонами 2  м. и 10м. Каждое боковое ребро пирамиды равно 10м. Найдите высоту пирамиды.
26. Все боковые грани треугольной пирамиды составляют с плоскостью основания угол 450. Найдите высоту пирамиды, если стороны основания равны 20, 21 и 29см.
27. В основании пирамиды лежит равнобедренная трапеция, основания которой равны 16 и 4см. Найдите высоту пирамиды, если каждая её боковая грань составляет с плоскостью основания угол 600.
28. Основанием пирамиды является равнобедренный треугольник с углом 1200. Боковые рёбра образуют с её высотой, равной 16см., углы в 450. Найдите площадь основания пирамиды. м. и 10м. Каждое боковое ребро пирамиды равно 10м. Найдите высоту пирамиды.
26. Все боковые грани треугольной пирамиды составляют с плоскостью основания угол 450. Найдите высоту пирамиды, если стороны основания равны 20, 21 и 29см.
27. В основании пирамиды лежит равнобедренная трапеция, основания которой равны 16 и 4см. Найдите высоту пирамиды, если каждая её боковая грань составляет с плоскостью основания угол 600.
28. Основанием пирамиды является равнобедренный треугольник с углом 1200. Боковые рёбра образуют с её высотой, равной 16см., углы в 450. Найдите площадь основания пирамиды.
|
| 3.3 ДОПОЛНИТЕЛЬНЫЕ ЗАДАНИЯ |
| 1. На поверхности геометрических тел нарисованы различные узоры. Изобразите развёртки поверхностей этих тел и покажите на них соответствующие узоры. |
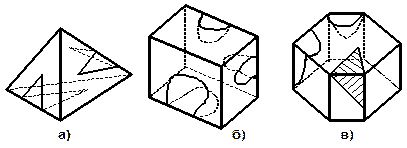 2. Постройте развёртку поверхности:
1) прямоугольного параллелепипеда с рёбрами 5см, 2см, 3см.;
2) прямого параллелепипеда, если его высота равна 6см и основанием является: а) параллелограмм, один из углов которого равен 500 и стороны –
а) 4,6см и 2см.;
б) ромб с углом 600 и меньшей диагональю 4см.
3)прямой призмы, если её высота равна 5см и в основании лежит:
а) трапеция АВСD, причём AD||ВС, ÐА=600, АВ=ВС= 2см, AD=5см;
б) равнобедренный треугольник, с основанием 4см и боковой стороной 2,5см.
4) правильной призмы, если её высота равна 6см и в основании лежит:
а) пятиугольник, вписанный в окружность радиуса 3см;
б) шестиугольник со стороной 3см.
Склейте из всех этих развёрток модели различных призм.
3. Постарайтесь как можно быстрее определить, сколько в каждом сооружении не хватает кубиков до полного куба.
2. Постройте развёртку поверхности:
1) прямоугольного параллелепипеда с рёбрами 5см, 2см, 3см.;
2) прямого параллелепипеда, если его высота равна 6см и основанием является: а) параллелограмм, один из углов которого равен 500 и стороны –
а) 4,6см и 2см.;
б) ромб с углом 600 и меньшей диагональю 4см.
3)прямой призмы, если её высота равна 5см и в основании лежит:
а) трапеция АВСD, причём AD||ВС, ÐА=600, АВ=ВС= 2см, AD=5см;
б) равнобедренный треугольник, с основанием 4см и боковой стороной 2,5см.
4) правильной призмы, если её высота равна 6см и в основании лежит:
а) пятиугольник, вписанный в окружность радиуса 3см;
б) шестиугольник со стороной 3см.
Склейте из всех этих развёрток модели различных призм.
3. Постарайтесь как можно быстрее определить, сколько в каждом сооружении не хватает кубиков до полного куба.
|
| 4. Какие предметы или фигуры можно получить, если сложить несколько: а) пирамид одинаковой величины; б) призм одинаковой величины. По возможности сделайте рисунок. 5. От деревянных моделей пирамид и призмы отпилили по кусочку разной формы, а оставшиеся части изобразили на рисунке. Нарисуйте отпиленные кусочки.
6. Постройте развёртку поверхности правильной пирамиды, боковое ребро которой равно 5,5см, а основание является: а) равносторонним треугольником со стороной 4,3см; б) квадратом с диагональю 5см; в) ромбом со стороной 4см и одним из углов, равным 850; г) правильный шестиугольник со стороной 3см. Склейте из всех этих развёрток модели пирамид.
7. Вам предлагается 12 равносторонних треугольников и 6 прямоугольников. Развёртки каких многогранников можно получить в результате соединения в разном порядке данных фигур.
8. На какие многогранники разбивает призму АВСА1В1С1 плоскость, проходящая через вершины А, В и С1? Какие особенности имеют эти многогранники? Сделайте рисунок. 9. В кубе АВСDА 1В 1С 1D1 из вершины D1 проведены диагонали граней D1A, D1B1, D1C. Как называется многогранник с вершинами D1, А, В1, С? Имеет ли этот многогранник равные рёбра? равные грани? 10. Вершинами некоторого многогранника являются центр верхней грани куба и середины всех сторон нижней его грани. Как называется этот многогранник? Сделайте рисунок и обозначьте равные рёбра многогранника; укажите, какие грани этого многогранника равны между собой. 11. Дана треугольная пирамида SАВС, АВС – основание. Точки М и N принадлежат основанию пирамиды, но не лежат на рёбрах АВ, ВС, АС. Покажите на рисунке сечение этой пирамиды плоскостью, проходящей через точки S, М и N. | |||||
| 12. В этих рисунках допущены ошибки. Найдите и исправьте их.
13. Дана прямая треугольная призма АВСА1В1С1: точка К – середина ребра А1В1, точки М и N – внутренние точки отрезков АВ и ВС, не совпадающие с их серединами. Покажите на рисунке сечение этой призмы плоскостью, проходящей через точки К, М, N. 14. В каждой строке написано пять слов, из которых четыре можно объединить в одну группу и дать ей название, а одно слово к этой группе не относится. Найдите это слово и назовите оставшуюся группу. 1) Призма, куб, пирамида, параллелепипед, прямоугольный параллелепипед. 2) Вершина, куб, ребро, основание, высота. 3) Призма, куб, октаэдр, тетраэдр, додекаэдр. 4) Ромб, треугольник, прямоугольник, пирамида, трапеция.
| |||||
| 15. Постарайтесь как можно быстрее определить, сколько многогранников изображено на рисунке? Назовите их.
| |||||
|
ТЕЛА ВРАЩЕНИЯ | |||||
|
ЦИЛИНДР | |||||
|
Прямым круговым цилиндром называется фигура, полученная при вращении прямоугольника вокруг оси, содержащей одну из его сторон.
|
Элементы цилиндра: R - радиус основания; D - диаметр основания; ОО1- ось вращения цилиндра; Н- высота; L – образующая. | ||||
|
ABCD- осевое сечение |
Круг k – поперечное сечение |
Усеченный цилиндр | |||
|
КОНУС | |||||
|
Прямым круговым конусом называется фигура, полученная при вращении прямоугольного треугольника вокруг оси, содержащий его катет. |
Элементы конуса: R – радиус основания; D – диаметр основания; Н – высота; L – образующая.
| ||||
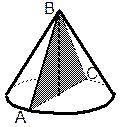 АВС – осевое сечение (равнобедренный треугольник)
АВС – осевое сечение (равнобедренный треугольник)
|
Круг k – поперечное сечение |
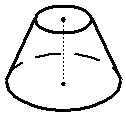 Усеченный конус
Усеченный конус
| |||
| ШАР |
СФЕРА | |||
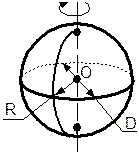 Шар – тело, получаемое вращением полукруга того же радиуса вокруг прямой, содержащий диаметр, ограничивающий этот полукруг.
R – радиус полукруга (равен радиусу шара).
D – диаметр шара.
О – центр шара.
Шар – тело, получаемое вращением полукруга того же радиуса вокруг прямой, содержащий диаметр, ограничивающий этот полукруг.
R – радиус полукруга (равен радиусу шара).
D – диаметр шара.
О – центр шара.
|
Сфера (шаровая поверхность) – замкнутая поверхность, получаемая вращением полуокружности вокруг прямой, содержащей стягивающий ее диаметр.
R – радиус сферы. О – центр сферы. | |||
|
УПРАЖНЕНИЯ | ||||
| 1. Ответьте на вопросы. 1. Какие фигуры изображены на рисунке?
2. Имеет ли цилиндр: а) центр симметрии? б) ось симметрии, сколько? в) плоскость симметрии, сколько? 3. Как расположены точки на поверхности цилиндра, равноудаленные от двух точек оснований? 4. Имеет ли конус: а) центр симметрии? б) ось симметрии, сколько? в) плоскость симметрии, сколько? 5. Как расположены точки на поверхности цилиндра, равноудаленные от двух точек образующих? Сделайте рисунок. 6. Имеет ли шар: а) центр симметрии? б) ось симметрии, сколько? в) плоскость симметрии, сколько? 7. Сколько касательных плоскостей к сфере можно провести через точку, взятую: а) на сфере; б) вне сферы. 2. Три шара радиуса R касаются друг друга. Вычислите стороны треугольника, образованного центрами этих шаров.
| ||||
| 3. Нарисуйте тела вращения, образованные вращением плоских фигур вокруг оси m, изображенных на рисунке.
4. Выберите верный ответ. К каждому заданию сделайте рисунок. 1. Радиус основания цилиндра 1.5см, высота – 4см. Чему равна диагональ осевого сечения? а) 4.2см; б) 10см; в) 5см. 2. Осевое сечение цилиндра – квадрат, площадь которого36дм2. Чему равна площадь основания цилиндра? а) 6p дм2; б) 9p дм2; в) 36p дм2. 3. Квадрат со стороной 4см вращается вокруг одной из своих сторон. Чему равна площадь основания полученного тела вращения? а) 2p см2; б) 4pсм2; в) 16p см2. 4. Наибольший угол между образующими конуса 600. Чему равен диаметр основания, если образующая равна 7см? 5. Площадь осевого сечения конуса равна 36см2, а высота 12см. Найдите радиус основания. а) 3см; б) 6см; в) 8см. | ||||
| 5. Точки Аи В расположены на видимой части боковой поверхности цилиндра. Скопируйте рисунок и проведите отрезок АВ. Все ли точки отрезка АВ принадлежат боковой поверхности цилиндра? | 
| |||
| 6. Точка А принадлежит основанию конуса, изображённого на рисунке, а точка В – оси SO этого конуса. Скопируйте рисунок и определите, где, внутри или снаружи конуса, расположена точка С прямой АВ. |
| |||
| 7. Точка А принадлежит основанию цилиндра, изображённого на рисунке, а точка В – оси ОО1 этого цилиндра. Скопируйте рисунок и определите, где, внутри или снаружи цилиндра, расположена точка С прямой АВ. |
| |||
|
ПРОЧИТАЙТЕ УСЛОВИЕ ЗАДАЧ И РАЗБЕРИТЕ ИХ РЕШЕНИЕ | ||||
| 1. Осевым сечением цилиндра является квадрат, диагональ которого равна 8 | ||||
Дано:
цилиндр;
АВСD – осев. сеч.;
АВСD – квадрат;
АС= 8  см.
Найти:
Sос. сеч. ; Sосн. см.
Найти:
Sос. сеч. ; Sосн.
|
| Решение:
1) Sос. сеч = SАВСD = АВ2.
Если АВСD – квадрат, то по теореме Пифагора АС = АВ  = 8 = 8  Þ Þ
| ||
| АВ =8(см). Тогда Sос. сеч = 82 = 64(см2). 2) Sосн. = pR2. Так как АВСD – осевое сечение, то R = Ответ: Sос. сеч. = 64см2, Sосн. = 32p. | ||||
| 2. Образующая конуса наклонена к плоскости основания под углом 300. Найдите высоту конуса и площадь осевого сечения, если образующая конуса равна 12мм. | ||
| Дано: конус; АВС – осев. сеч.; L = АВ = 12мм; ÐВАС = 300. Найти: Н, Sос. сеч. . | 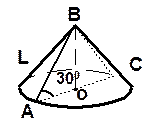
| Решение: 1) Найдём высоту. Для этого рассмотрим D АОВ – он прямоугольный, т. к. ВО – высота. Значит, если АВ = 12(мм), то ВО =12 : 2 = 6(мм). ВО = Н. |
| 2) Sос. сеч. = SDАВС = АС - ? АС = 2АО. Найдём АО из D АОВ по т. Пифагора. АО2 =АВ2 – ВО2 = = 122 – 62 = 108, АО = Тогда Sос. сеч.= Ответ: Н = 6мм, Sос. сеч = 36 3. На расстоянии 8дм от центра шара проведено сечение, площадь которого равна 36дм2. Найдите радиус шара. | ||
Дано:
шар, a 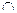 шар ;
Scеч. = 36дм2;
h = ОА = 8дм;
Найти: Rш. шар ;
Scеч. = 36дм2;
h = ОА = 8дм;
Найти: Rш.
|
| Решение: 1) Scеч. = pR2 = 36 Þ Rсеч. = 6дм. Rш. - ? Рассмотрим DОАВ, где АВ = Rсеч., ОВ = Rш. и ОА = h, тогда по т. Пифагора |
| ОВ2 = ОА2 + АВ2 = 82 + 62 = 100, ОВ = Ответ: Rш. =10дм. | ||
| РИСУНКИ К ЗАДАЧАМ |
|
| 4.2 ЗАДАЧИ |
| 1. Радиус основания цилиндра равен 5см, а его образующая – 9см. Найдите: площадь основания цилиндра, площадь осевого сечения, диагональ осевого сечения. 2. Высота цилиндра равна 8см, радиус равен 5см. Найдите площадь сечения цилиндра плоскостью, параллельной его оси, если расстояние между этой плоскостью и осью цилиндра равно 3см. |
3. Осевое сечение конуса – равносторонний треугольник со стороной 6дм. Найдите высоту конуса, площадь осевого сечения и основания.
4. Найдите площадь основания и площадь осевого сечения тела, полученного при вращении прямоугольного треугольника с катетом 3см и прилежащим углом 300 вокруг меньшего катета.
5. Радиусы оснований усечённого конуса равны 5дм и 11дм, а образующая равна 10дм. Найдите: а) высоту усечённого конуса; б) площадь осевого сечения.
6. Радиус сферы равен 112см. Точка, лежащая на плоскости, касательной к сфере, удалена от точки касания на 15см. Найдите расстояние от этой точки до ближайшей к ней точки сферы.
7. Угол между высотой цилиндра и диагональю осевого сечения равен 600. Найдите площадь осевого сечения и площадь основания цилиндра, если длина диагонали осевого сечения – 24мм.
8. Высота цилиндра равна 12м. а радиус основания равен 10м. Цилиндр пересечён плоскостью, параллельной его оси, так, что в сечении получился квадрат. Найдите расстояние от оси цилиндра до секущей плоскости.
9. Осевое сечение конуса – прямоугольный треугольник. Найдите площадь этого сечения и высоту конуса, если радиус основания конуса равен 5  см.
10. Найдите площадь основания и площадь осевого сечения тела, полученного при вращении квадрата вокруг одной из сторон. Диагональ квадрата равна 6 см.
10. Найдите площадь основания и площадь осевого сечения тела, полученного при вращении квадрата вокруг одной из сторон. Диагональ квадрата равна 6  см.
11. Радиус основания конуса равен 14м. Найдите площадь сечения, проведённого перпендикулярно его высоте через её середину. см.
11. Радиус основания конуса равен 14м. Найдите площадь сечения, проведённого перпендикулярно его высоте через её середину.
|
12. Найдите площадь сечения шара радиуса 41см, проведённого на расстоянии 9см от центра.
13. На расстоянии 6дм от центра шара проведено сечение, площадь которого равна 64дм2. Найдите радиус шара.
14. Радиусы оснований усечённого конуса равны 1м и2м, высота – 3м. Найдите площадь осевого сечения.
15. Угол между высотой конуса и образующей равен 300. Найдите образующую и площадь осевого сечения конуса, если радиус основания равен 5м.
16. Найдите площадь основания и площадь осевого сечения тела, полученного при вращении равнобедренного прямоугольного треугольника с катетом 6см вокруг его оси симметрии.
17. Площадь основания цилиндра – 5м2, а площадь осевого сечения – 10м2. Найдите высоту цилиндра и диагональ осевого сечения.
18. Высота цилиндра равна 10дм. Площадь сечения плоскостью параллельной оси цилиндра и удалённой на 9дм от неё равна 240дм2. Найдите радиус цилиндра.
19. Образующая конуса равна 25м, а диаметр основания - -48м. Найдите площадь основания и осевого сечения конуса.
20. Осевым сечением цилиндра является квадрат, диагональ которого равна 3  см. Найдите площадь осевого сечения и площадь основания цилиндра.
21. Найдите площадь основания и площадь осевого сечения тела, полученного при вращении прямоугольника со сторонами 34м и 6м вокруг прямой, проходящей через середины его больших сторон.
22. Радиусы оснований усечённого конуса равны 10м и 8м, а образующая составляет с плоскостью основания угол в 450. Найдите площадь осевого сечения.
23. Сферу на расстоянии 8м от центра пересекает плоскость. Радиус сечения равен 15м. Найдите радиус сферы.
24. Диаметр основания цилиндра – 30см. Цилиндр пересечён плоскостью, параллельной его оси, так, что в сечении получился квадрат. Расстояние от оси цилиндра до секущей плоскости – 12см. Найдите площадь сечения. см. Найдите площадь осевого сечения и площадь основания цилиндра.
21. Найдите площадь основания и площадь осевого сечения тела, полученного при вращении прямоугольника со сторонами 34м и 6м вокруг прямой, проходящей через середины его больших сторон.
22. Радиусы оснований усечённого конуса равны 10м и 8м, а образующая составляет с плоскостью основания угол в 450. Найдите площадь осевого сечения.
23. Сферу на расстоянии 8м от центра пересекает плоскость. Радиус сечения равен 15м. Найдите радиус сферы.
24. Диаметр основания цилиндра – 30см. Цилиндр пересечён плоскостью, параллельной его оси, так, что в сечении получился квадрат. Расстояние от оси цилиндра до секущей плоскости – 12см. Найдите площадь сечения.
|
 25. Площадь основания цилиндра 16p см2. Угол между образующей цилиндра и диагональю его осевого сечения равен 300. Найдите площадь и диагональ осевого сечения.
26. Цилиндр пересечён плоскостью, параллельной его оси, на расстоянии 5мм. Найдите высоту цилиндра, если диаметр основания – 26мм, а площадь сечения – 240мм.
27. Образующая конуса наклонена к плоскости основания под углом 600. Найдите высоту конуса и площадь осевого сечения , если радиус основания равен 9мм..
28. Найдите площадь основания и площадь осевого сечения тела, полученного при вращении прямоугольника со сторонами 14м и 6м вокруг меньшей стороны.
29. Найдите образующую усечённого конуса, если радиусы оснований равны 3см и 6см, а высота равна 4см.
30. Вершины равностороннего треугольника лежат на сфере радиуса 13см. Найдите расстояние от центра сферы до плоскости треугольника, если сторона треугольника равна 10 25. Площадь основания цилиндра 16p см2. Угол между образующей цилиндра и диагональю его осевого сечения равен 300. Найдите площадь и диагональ осевого сечения.
26. Цилиндр пересечён плоскостью, параллельной его оси, на расстоянии 5мм. Найдите высоту цилиндра, если диаметр основания – 26мм, а площадь сечения – 240мм.
27. Образующая конуса наклонена к плоскости основания под углом 600. Найдите высоту конуса и площадь осевого сечения , если радиус основания равен 9мм..
28. Найдите площадь основания и площадь осевого сечения тела, полученного при вращении прямоугольника со сторонами 14м и 6м вокруг меньшей стороны.
29. Найдите образующую усечённого конуса, если радиусы оснований равны 3см и 6см, а высота равна 4см.
30. Вершины равностороннего треугольника лежат на сфере радиуса 13см. Найдите расстояние от центра сферы до плоскости треугольника, если сторона треугольника равна 10 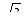 см.
31. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 600. Образующая цилиндра равна 10 см.
31. Плоскость, параллельная оси цилиндра, отсекает от окружности основания дугу в 600. Образующая цилиндра равна 10 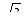 см, расстояние от оси до секущей плоскости равно 2см. Найдите площадь сечения.
32. Площадь основания цилиндра относится к площади осевого сечения как см, расстояние от оси до секущей плоскости равно 2см. Найдите площадь сечения.
32. Площадь основания цилиндра относится к площади осевого сечения как 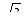 p : 4. Найдите угол между диагоналями осевого сечения.
33. Найдите угол при вершине осевого сечения конуса, если развёрткой его боковой поверхности является сектор с дугой, равной 1800.
34. Вычислите площадь основания и высоту конуса, если развёрткой его боковой поверхности является сектор, радиус которого равен 9см, а дуга равна 1200.
35. Сфера касается граней двугранного угла в 1200. Найдите радиус сферы и расстояние между точками касания, если расстояние от центра сферы до ребра двугранного угла равно а. p : 4. Найдите угол между диагоналями осевого сечения.
33. Найдите угол при вершине осевого сечения конуса, если развёрткой его боковой поверхности является сектор с дугой, равной 1800.
34. Вычислите площадь основания и высоту конуса, если развёрткой его боковой поверхности является сектор, радиус которого равен 9см, а дуга равна 1200.
35. Сфера касается граней двугранного угла в 1200. Найдите радиус сферы и расстояние между точками касания, если расстояние от центра сферы до ребра двугранного угла равно а.
|
| 4.3 ДОПОЛНИТЕЛЬНЫЕ ЗАДАНИЯ |
| 1. В цилиндре диаметром 15мм сделано цилиндрическое отверстие диаметром 5мм. Оси обоих цилиндров совпадают. Затем цилиндр разрезали пополам плоскостью, проходящей через ось. Нарисовать и указать размеры получившегося тела. |
2. От деревянных моделей цилиндра и конуса отпилили по кусочку разной формы, оставшиеся части изобразили на рисунке.
 Нарисуйте развёртку поверхности срезанной части для каждой модели.
3. На поверхности геометрических тел нарисованы различные узоры.
Нарисуйте развёртку поверхности срезанной части для каждой модели.
3. На поверхности геометрических тел нарисованы различные узоры.
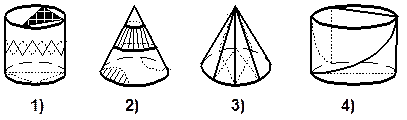 Изобразите развёртки поверхностей этих тел и покажите на них соответствующие узоры.
4. Постройте развёртку поверхности:
1) цилиндра
а) диаметр которого равен 40мм, а высота 5см;
б) в осевом сечении которого лежит прямоугольный треугольник со сторонами 3см и 4см (2 варианта);
в) в осевом сечении которого лежит квадрат с диагональю 6
Изобразите развёртки поверхностей этих тел и покажите на них соответствующие узоры.
4. Постройте развёртку поверхности:
1) цилиндра
а) диаметр которого равен 40мм, а высота 5см;
б) в осевом сечении которого лежит прямоугольный треугольник со сторонами 3см и 4см (2 варианта);
в) в осевом сечении которого лежит квадрат с диагональю 6 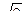 см. см.
|
2) конуса
а) радиусом 3см и образующей 80мм;
б) полученного при вращении прямоугольного треугольника с катетами 0,6дм и 8см (2 вида);
в) в осевом сечении которого лежит равносторонний треугольник со стороной 0, 04м;
г) диаметр которого равен 30мм, а образующая наклонена к плоскости основания под углом 300;
3) усечённого конуса
а) радиусы которого 30мм и 0,5дм, а высота 4см;
б) больший радиус которого равен 0,03м, высота 0,2дм, а образующая наклонена к плоскости основания конуса под углом 300;
в) отношение большего радиуса к меньшему 1: 2 и образующая наклонена к плоскости основания под углом 300.
5. На каждом рисунке выберите основные детали и объясните, почему вы считаете их основными.
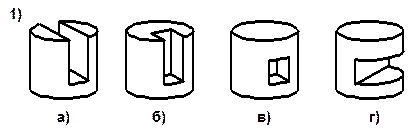
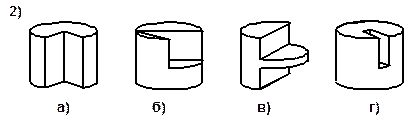 Можно ли из них получить любую другую деталь, изображённую на этом же рисунке?
Можно ли из них получить любую другую деталь, изображённую на этом же рисунке?
|
6. В каждой строке написано пять слов, из которых четыре можно объединить в одну группу и дать ей название, а одно слово к этой группе не относится. Найдите это слово и назовите оставшуюся группу.
1) Образующая, высота, ось, апофема, радиус.
2) Квадрат, треугольник, конус, круг, эллипс.
3) Вершина, конус, цилиндр, пирамида, призма.
4) Ребро, радиус, образующая, высота, диаметр.
5) Грань, ребро, высота, основание, образующая.
7. Перечислите фигуры, изображённые на рисунке.

|
| 5 ПЛОЩАДЬ ПОВЕРХНОСТИ И ОБЪЁМ ТЕЛ ВРАЩЕНИЯ И МНОГОГРАННИКОВ О ПОНЯТИИ ТЕЛА, ЕГО ПОВЕРХНОСТИ И ОБЪЁМА В ГЕОМЕТРИИ |
| Геометрическое тело – часть пространства, обычно ограниченная, то есть принадлежащая, например, некоторому шару. Другими знакомыми нам примерами тел являются многогранник, цилиндр и конус. Поверхность – одно из основных геометрических понятий. В элементарной математике рассматриваются плоскости, многогранные, а также некоторые кривые поверхности. Поверхность - граница тела. |
| Объём – одна из основных величин, связанных с геометрическими телами. В простейших случаях измеряется числом умещающихся в теле единичных кубов, то есть кубов с ребром, равным единице длины. Объём простого тела Тело называется простым, если его можно разбить на конечное число треугольных пирамид. Примером простого тела является любой выпуклый многогранник. Объём – это положительная величина, численное значение которой обладает следующими свойствами: 1. Равные тела имеют равные объёмы. 2. Если тело разбито на части, являющиеся простыми телами, то объём этого тела равен сумме объёмов его частей. 3. Объём куба, ребро которого равно единице длины, равен единице. Два тела называются равновеликими, если они имеют равные объёмы. Объём произвольного тела Данное тело имеет объём V, если существуют содержащие его простые тела и содержащиеся в нём простые тела с объёмами, сколь угодно мало отличающимися от V. Современная трактовка измерения объёмов сводится к следующему. Рассматриваются всевозможные многогранники, вписанные в тело К, и всевозможные многогранники, описанные вокруг тела К. Вычисление объёма многогранника сводится к вычислению объёмов, составляющих его тетраэдров. |
ПЛОЩАДЬ ПОВЕРХНОСТИ И ОБЪЁМ ПРИЛОЖЕНИЕ | ||
|
РАЗВЁРТКИ ФИГУР Развёртка многогранника – совокупность многоугольников, для которых указано, как следует их соединить друг с другом по сторонам и вершинам, чтобы получить данный многогранник, грани которого – эти многоугольники. Развёртку многоугольника можно получить, сделав предварительно один или несколько разрезов её по рёбрам таким образом, чтобы он не распался на отдельные куски, и уложив полученное на плоскость. Аналогично можно уложить на плоскость коническую и цилиндрическую поверхность.
| ||

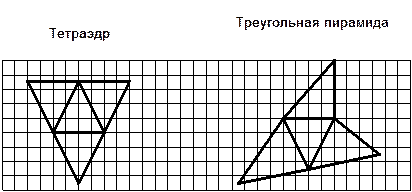
| ||
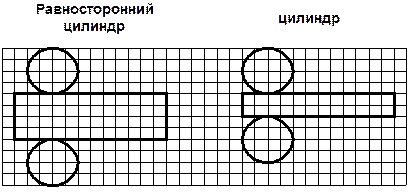
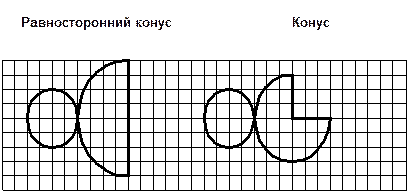
|
Ответы
Задача
рисунок
Ответ
1.1
М
2
2.2
Дм
3
3.3
8 
4
2.1
Дм
5
1.3
8м
6
2.4
Мм
7
3.2
М
8
3.1
Дм
9
4.1
18м;
М
10
2.3
16мм;
Мм
11
1.4
См
12(а)
4.2
21дм;
Дм
12(б)
4.4
2см;
См
13
3.4
8м
14
1.2
Мм
15
4.3
Мм
16(а)
5.2
3м
16(б)
5.3
5 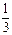
16(в)
5.4
См
16(г)
5.1
См
3.1
М
135м2
2.3
См
30см2
1.1
Дм
4.1
5м
5.3
М
1.2
 дм
дм
2.1
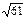 см
см
3 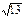 см2
см2
5.4
М
3.2
5 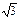 см
см
25 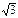 см2
см2
4.4
12 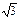 дм
дм
3.5
Дм
80дм2
5.2
См
1.3
Мм
4.2
2 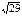 м
м
2.2
2 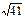 м
м
8 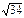 м2
м2
16
2.5
12см,7 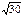
17
3.4
16м,64 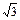
18
1.5
7м
19
4.3
Дм
20
1.4
4м
21
3.3
12 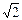
108м2
22
4.5
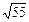
23
2.4
5 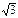 ,25дм2
,25дм2
24
5.1
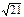 м
м
25
1.5
М
Призма
1
1.4
108м2
2
2.1
См
3
3.1
120 ´ (2+ 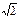 )
)
4
4.2
Дм
5
4.4
2 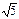
6
5.3
15 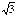
7
1.2
100см2
8
3.2
М
9
4.1
См
10
5.5
6м
11
1.1
6 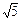
12
2.2
16 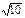
13
3.4
48 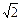
14
4.5
8 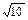
15
5.1
13
16
1.3
12 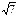
17
2.4
М
18
4.3
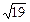
19
1.5
4 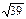
20
5.2
2 
21
2.3
М
3.5
32 ´
(2+ 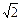 )
)
5.4
4 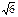 см
см
2.5
8 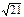
3.3
45(2+ 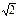 )
)
Пирамида
1
2.1
См
2
1.3
5м
3
3.2
16 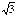 м
м
4
4.1
Мм
5
5.1
7,5м2
6
3.5
Мм
7
2.5
20 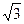
8
1.4
Дм
9
2.4
2 
10
5.2
Дм
11
3.3
3 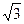
12
4.2
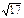
13
1.1
5 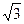
14
2.2
4м
15
3.1
2 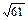
16
5.5
20 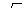
17
4.3
М
18
5.3
225;100;
25см2
19
1.2
См
20
2.3
5м
21
5.4
21м2
22
4.4
8м
23
3.4
2 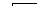
24
4.5
7м
25
1.5
8м
Тела вращения
1
1.1
90см2
25 p см2
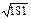 см
см
2
2.1
64см2
3
3.4
3 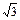 дм
дм
9 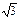 дм2
дм2
36 p дм2
4
4.2
9 p см2
13,5 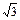
5
5.3
128дм2
6
6.3
См
7
1.5
144 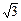
36 p мм2
8
2.3
8м
9
3.3
50см2
5 
10
4.1
36 p см2
72см2
11
5.1
49 p м2
12
6.1
400 p см2
13
6.5
Дм
14
5.2
9м2
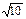 м
м
15
3.5
М
25 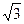
16
4.4
18 p см2
36см2
17
1.4
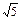 м
м
5м
18
2.2
Дм
19
3.1
84м2
144 p м2
20
1.2
9 см2
25 p см2
21
4.3
P
204м2
22
5.4
18 м2
23
6.2
М
24
2.5
324 см2
25
1.3
См
64 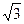
26
2.4
Мм
27
3.2
9 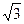
81 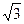
28
4.5
P
168 см2
29
5.5
См
30
6.4
См
Площадь поверхности и объём
| задание | ответ | ||
|
Призмы | |||
|
1.1 | 512см2 | ||
|
1.2 | 64  см3 см3
| ||
|
1.3 | 6,25  м3 м3
| ||
|
1.4 | 384см2 | ||
|
1.5 | 188м2 | ||
|
1.6 | 2 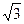 м3 м3
| ||
|
1.7 | - | ||
|
1.8 | 24 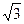 +220 +220
| ||
|
1.9 | 108+36 
| ||
|
1.10 | 144  см3 см3
| ||
|
Пирамиды | |||
|
2.1 | 81 | ||
|
2.2 | 360см2 | ||
|
2.3 | 228 | ||
|
2.4 | 64см3 | ||
|
2.5 | 32м3 | ||
|
2.6 | 900( | ||
|
2.7 | 8 | ||
|
2.8 | 9( | ||
|
2.9 | 1470 | ||
|
2.10 |
Н | ||
|
2.11 | 2,5(1,5 | ||
|
Цилиндра | |||
| 3.1 | 54 p см2 | ||
| 3.2 | 120 p см2 | ||
| 3.3 | 150 p м3 | ||
| 3.4 | 20 p см2 | ||
| 3.5 | 8 p дм3 | ||
| 3.6 | 85,75 p дм3 | ||
| 3.7 | 216 p см3 | ||
| 3.8 | 270 p дм2 | ||
| 3.9 | 32 p м3 | ||
|
Конуса | |||
|
4.1 | 1344 p м3 | ||
|
4.2 | 90 p дм2 | ||
|
4.3 | 75 p м2 | ||
|
4.4 | | ||
|
4.5 | 3 | ||
|
4.6 | 50 ´ p (1+ | ||
|
4.7 | 27 p дм3 | ||
|
4.8 | 144 ´ (3+2 | ||
|
4.9 | 96 p м2 | ||
|
4.10 | | ||
|
4.11 | 3 p ´ (3+ | ||
|
Сферы, шара | |||
| 5.1 | 91894 | ||
| 5.2 | 1156 p м2 | ||
| 5.3 |
P /3 | ||
| 5.4 | 32 p /3 дм2 | ||
СПИСОК ЛИТЕРАТУРЫ
1 Алёшина Т.Н. Обучающие и проверочные задания. Геометрия. 10 класс, 11 класс. М.: Интеллект-центр, 1999.
2 Башмаков М.И. Математика: Экспериментальное учебное пособие для СПТУ. М.: Высшая школа, 1987.
3 Брагин В.Г., Грабовский А.И. Все предметы школьной программы в схемах и таблицах. Алгебра. Геометрия. М.: Олимп, 1996.
4 Гарднер М. Математические головоломки и развлечения. М: Мир, 1971.
5 Гейденштейн Л.Э., Ершова А.П. Наглядный справочник по геометрии для 7-11 классов. М., Харьков: Илекса, Гимназия, 1999.
6 Денищева Л.О., Михеева Т.Ф. Учимся решать задачи. Геометрия 10-11 класс. М.: Интеллект-центр, 1998.
7 Домбровская Т.В. Тестовые задания по геометрии (по учебнику Погорелова А.В.). 10 класс, 11 класс. Томск: 1999.
8 Дорофеев Г.В., Муравин Г.К., Седова Е.А. Сборник заданий для подготовки и проведения письменного экзамена по математике (курс А) и алгебре и началам анализа (курс В) за курс средней школы 11 класс. М.: Дрофа, 1999.
Никольский С.М. Школьная энциклопедия. Математика. М.: Большая Российская энциклопедия, 1996.
9 Панчищина В.А., Гельфман Э.Г., Ксенева В.Н. и др. Геометрия. Части I-III. Томск: Изд-во ТГУ, 2002.
10 Тихомирова Л.Ф. Развитие познавательных способностей детей. Ярославль: Академия развития, 1997.
НАГЛЯДНОЕ ПОСОБИЕ
ПО ГЕОМЕТРИИ
Учебное пособие для старшеклассников
Северск 2015
| УТВЕРЖДАЮ Зам. директора по НУМР ___________Г.В. Скорик ____ ____________2015 г. | УТВЕРЖДЕНО ОМС ___ ________2015г. |
Рецензенты: М.С. Бухтяк, к.ф.-м. н., доц.;
В.Е. Шутеева, отличник просвещения,
засл. учитель России, учитель-методист.
Авторы:
Поликарпова Н. С. преподаватель,
Сазанова Т. А., заведующий кафедрой естественно математического образования ТОИПКРО, канд. техн. наук, доцент.
Наглядное пособие по геометрии. - Учебное пособие. 2-е изд., испр. и доп. Северск, 2015. - 120 с.
Учебное пособие предназначено для обучающихся средней школы, оно призвано помочь усвоить курс геометрии. Может быть полезно абитуриентам, студентам профессиональных образовательных организаций, преподавателям при изучении, систематизации и повторении курса планиметрии. Особенностью пособия является наглядность во всех видах заданий. Пособие активизирует самостоятельную деятельность обучающихся, допускает дифференцированный подход в обучении и может быть использовано в предпрофильных и профильных классах.
Рассмотрено на заседании цикловой комиссии
Общеобразовательных дисциплин
Протокол № 8 от «14» марта 2015 г.
Председатель цикловой комиссии Журова К.А.
Нормоконтроль: Лазуткина М.Г.
ВВЕДЕНИЕ
"Посредством глаза, но не глазом
смотреть на мир умеет разум"
Уильям Блейк
Своеобразие геометрии, которое выделяет ее из других разделов математики, да и всех областей науки вообще, заключается в неразрывном, органическом соединении живого воображения со строгой логикой. В своей сущности и основе геометрия и есть пространственное воображение, пронизанное и организованное строгой логикой. В ней всегда присутствуют эти два неразрывно связанных элемента - наглядная картина и точная формулировка, строгий логический вывод. Там, где нет одной из этих сторон, нет и подлинной геометрии.
Так писал о геометрии академик А.Д. Александров.
Наглядность, воображение принадлежат больше искусству, строгая логика - привилегия науки. Сухость точного вывода и живость наглядной картины - «лёд и пламень не столь различны меж: собой». Геометрия соединяет в себе эти противоположности, они в ней взаимно проникают, организуют и направляют друг друга. Это относится, в конечном счете, также к современным абстрактным геометрическим теориям, которые при всей своей возвышенной отвлеченности вырастают из той же геометрической интуиции. Стоит лишь вспомнить классические творения архитектуры, начиная с древнейших пирамид, как сразу становится очевидным, что геометрия в некотором смысле относится к искусству.
При изучении геометрии особое внимание уделяется развитию визуального мышления учащихся.
Основное правило состоит в том, что, встречаясь с определением, теоремой или задачей, необходимо, прежде всего, представить соответствующую геометрическую фигуру, сделать рисунок - это поможет понять содержание.
Каждому учителю математики хорошо знакомы те трудности, с которыми сталкивается школьник при переводе геометрической задачи на язык чертежа, он часто не может сделать рисунок или запомнить название фигуры, её элементов. Поэтому необходимы специальные приемы для формирования соответствующих умений у учащихся.
Основной задачей преподавателя является оказание помощи в переводе знаковой информации в визуальную, в создании образа данного знака, фигуры, рисунка.
Образ, как известно из психологии, - это помощник мысли, который облегчает понимание новых сложных объектов.
Если учащемуся предложить материал неизвестного ему содержания и непривычного оформления, то он не воспримет, не увидит ничего. Нельзя видеть, не понимая; слово "видеть" имеет два значения: зрительно воспринимать что-либо и понимать что-либо.
Известно, что степени "понимания" могут быть весьма различны: от смутного ощущения до полной ясности.
Значит, для того чтобы оптимизировать процесс усвоения материала, учителю необходимо растолковать ученику, как именно и в каком порядке он может рассматривать данный материал, чтобы иметь хотя бы относительную ясность, т. е. помочь ученику в поиске порядка в беспорядочности.
Как облегчить обучающемуся проникновение в содержание, значение предъявляемых зрительных образов?
При формировании первичного образа большое внимание уделяется качеству его изображения. Нельзя научить геометрии, показывая безграмотное оформление рисунков к задачам и теоремам. Образ должен быть сформирован и организован разумно, чтобы наиболее важные его свойства были ясно видимы.
Для дальнейшего формирования образа и развития визуального мышления необходима особая организация материала. Специальное расположение чертежей, графиков, формул позволяет ученику выстраивать их в системы, сравнивать визуальные комбинации с некоторым обобщённым образом. Это способствует развитию зрительных ориентиров (визуальных стандартов), которые в дальнейшем помогут в решении задач.
Активное и целенаправленное использование визуального мышления в процессе обучения основано на выработке устойчивых стандартных образов основных учебных понятий. Подготовка добротных геометрических изображений этих понятий, адекватно отражающих их основные черты, удобных в работе, пригодных для многократного использования, является первостепенной задачей.
Не следует стараться что-то заучить, не нарисовав, не вообразив того, о чём идёт речь. Поэтому каждая тема в предлагаемом пособии снабжена наглядным материалом, направленным на усвоение теории. Это способствует развитию образного мышления обучающихся, обогащает их представления о свойствах геометрических фигур, обеспечивает качество обучения.
Учебное пособие состоит из 6 разделов, каждый из которых включает в себя наглядный теоретический материал, подборку упражнений для закрепления, решение основных задач, задачи разного уровня и рисунки к ним.
Теоретический материал содержит основные определения, свойства, теоремы и формулы, необходимые в решении задач. Доказательство теорем опускается.
В разделе "Планиметрия" собран теоретический материал, необходимый для решения стереометрических задач. Целью этого раздела является изображение рисунков и изложение теории наглядно, доступно и в разумном порядке, для правильного формирования первичного образа.
Упражнения, представленные в каждом разделе, направлены на закрепление теоретического материала. Все они снабжены рисунками. Таким образом, формируется визуальный стандарт, который в дальнейшем помогает ученику в решении задач.
В каждом разделе предложено оформление и решение основных типов задач по теме. Все предложенные задачи соответствуют нескольким уровням усвоения знаний, причем сначала предложены рисунки к задачам, а затем в произвольном порядке условия к ним. Это сделано для того, чтобы ученик выбрал необходимый рисунок к задаче, а также обратил внимание на различное изображение фигур.
Под чертой даны задачи II-III уровня сложности. Из задач этого раздела можно составить разноуровневые контрольные работы.
В процессе решения ученику предлагаются готовые рисунки (номера задач и рисунков не совпадают). Это сделано для того, чтобы обучающиеся на первых порах не испытывали трудности в построении рисунка и привыкали к правильному изображению. Как только у обучающихся сформируется устойчивый визуальный образ (стандарт), необходимость обращения к данным рисункам отпадает.
Для развития творческих способностей ученику необходимо представить данный образ в нестандартной ситуации. Этой цели посвящены дополнительные задания в конце каждого раздела. Они направлены на развитие не только пространственного воображения, но и других интеллектуальных качеств. Ученик сам сможет выбрать интересующее его задание и тем самым расширить свои знания по данной теме.
На уроках геометрии для развития визуального мышления необходимо использовать игры, упражнения, тесты, развивающие внимание, наблюдательность, воображение и память. Задания развивающего характера также можно найти в пособии. В приложении даны развёртки, по которым обучающиеся смогут изготовить модели фигур.
Данное пособие призвано обеспечить дифференцированный подход к обучению, его можно использовать для организации самостоятельной и индивидуальной работы, для контроля знаний.
Особенность данного пособия в том, что здесь предложена система упражнений и заданий, направленных на развитие индивидуальных интеллектуальных возможностей обучающихся.
СОДЕРЖАНИЕ
1 Планиметрия. 9
1.1 Прямые и углы на плоскости. 9
1.2 Треугольники. 11
1.3 Четырёхугольники. 14
1.4 Окружность. 17
1.5 Основные формулы.. 19
1.6 Задачи. 22
2 Стереометрия. 27
2.1 Прямые и плоскости в пространстве. 27
2.2 Параллельность прямых и плоскостей. 30
2.3 Упражнения. 32
2.4 Задачи. 41
2.5 Дополнительные задания. 43
2.6 Перпендикулярность прямых и плоскостей. 47
2.7 Упражнения. 52
2.8 Задачи. 59
2.9 Дополнительные задания. 62
3 Многогранники. 65
3.1 Упражнения. 71
3.2 Задачи. 81
3.3 Дополнительные задания. 85
4 Тела вращения. 90
4.1 Упражнения. 93
4.2 Задачи. 98
5 Площадь поверхности и объём тел вращения и многоранников 103
5.1 Упражнения. 106
5.2 Задачи. 107
5.3 Дополнительные задания. 113
Приложения. 115
Ответы.. 118
Список литературы.. 120
ПЛАНИМЕТРИЯ
Так называется раздел геометрии, в котором изучаются фигуры
на плоскости.
ПРЯМЫЕ И УГЛЫ НА ПЛОСКОСТИ
ВИДЫ УГЛОВ
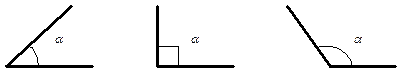 Острый угол Прямой угол Тупой угол
Острый угол Прямой угол Тупой угол
00 < a < 900 . a = 900 . 900 < a< 1800.
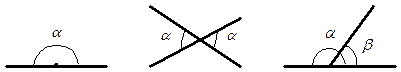 Развернутый угол Вертикальные углы Смежные углы
Развернутый угол Вертикальные углы Смежные углы
a = 1800. равны. a + b = 1800.
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
Так называются прямые, которые не пересекаются.
Дата: 2018-12-21, просмотров: 3012.

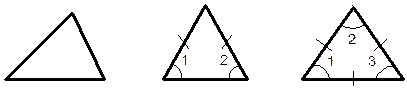 Разносторонний Равнобедренный Равносторонний
Разносторонний Равнобедренный Равносторонний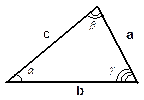
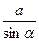 =
= 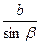 =
= 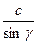 =2R,
=2R,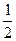 AC.
AC.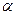 =
= 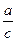 =
= 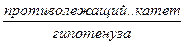 .
.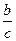 =
= 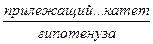 .
.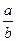 =
= 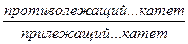 .
.
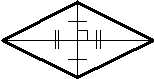
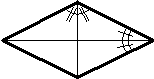

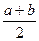 .
.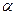 +
+ 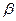 = 1800,
= 1800,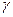 +
+ 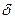 = 1800.
= 1800.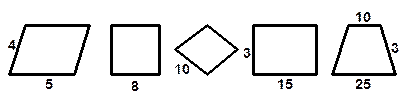
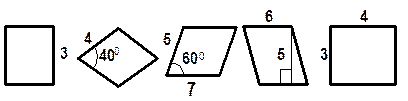

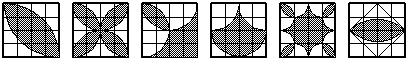
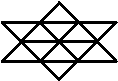
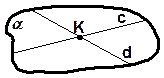
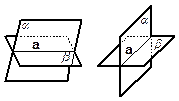
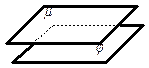
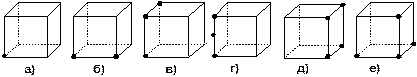
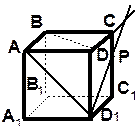
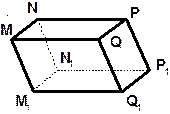
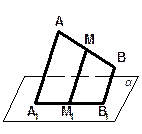
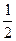 (АА1+ВВ1) =
(АА1+ВВ1) = 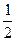 АС=
АС= 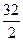 =16(дм.). РМНКР.=2(8+16)=48(дм.).
=16(дм.). РМНКР.=2(8+16)=48(дм.).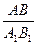 =
= 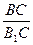 =
= 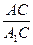 ;
; 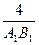 =
=  ; А1В1=
; А1В1= 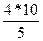 =8. Ответ: 8см.
=8. Ответ: 8см. 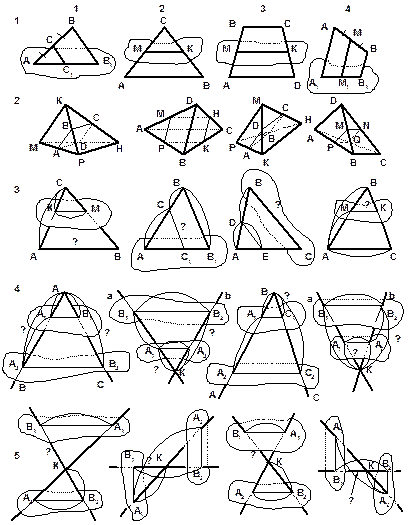
 в точке Е. Отрезок АDлежит в плоскости
в точке Е. Отрезок АDлежит в плоскости  . Скопируйте рисунок и изобразите отрезки АС и ВD. Определите, пересекаются ли эти отрезки? Ответ обоснуйте.
. Скопируйте рисунок и изобразите отрезки АС и ВD. Определите, пересекаются ли эти отрезки? Ответ обоснуйте.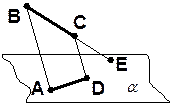
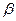 . Точка А принадлежит плоскости
. Точка А принадлежит плоскости 
 а) б) в)
а) б) в)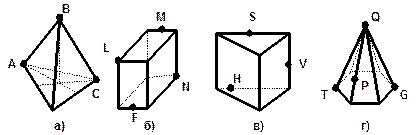

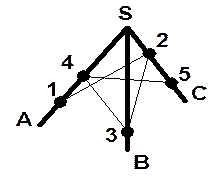
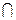 b = с. Прямая а ^ с, прямая b ^ c. Как расположены прямые a и b.
b = с. Прямая а ^ с, прямая b ^ c. Как расположены прямые a и b.
 АВС- правильный, OS – высота, O – центр вписанной окружности).
АВС- правильный, OS – высота, O – центр вписанной окружности).
 взаимно перпендикулярны. Через некоторую точку
взаимно перпендикулярны. Через некоторую точку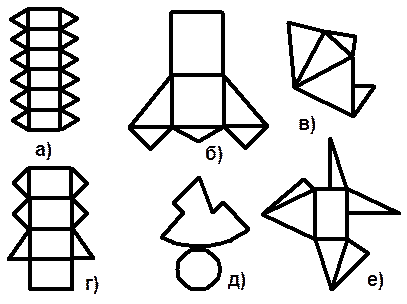 5. Изобразите параллелепипед ABCDA1B1C1D1 и отметьте точки M и N соответственно на рёбрах ВВ1 и СС1. Постройте точку пересечения: а) прямой MN с плоскостью АВС; б) прямой АМ с плоскостью А1В1С1.
5. Изобразите параллелепипед ABCDA1B1C1D1 и отметьте точки M и N соответственно на рёбрах ВВ1 и СС1. Постройте точку пересечения: а) прямой MN с плоскостью АВС; б) прямой АМ с плоскостью А1В1С1.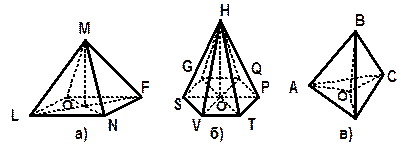

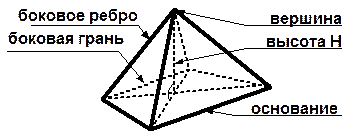
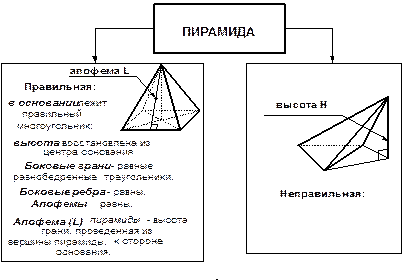


 АВС, по теореме Пифагора АС2 = АВ2 + ВС2 = 2 · АВ2 = 2·62 =72, АС =
АВС, по теореме Пифагора АС2 = АВ2 + ВС2 = 2 · АВ2 = 2·62 =72, АС = 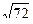 = 6
= 6 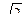 (дм). SАСС1А1 = 15·6
(дм). SАСС1А1 = 15·6 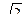 = 90( 2 +
= 90( 2 + 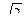 ) дм2.
) дм2. KMK1 = 450.
KMK1 = 450.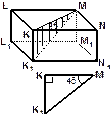
 KMK1, он прямоугольный (если
KMK1, он прямоугольный (если 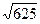 =25 дм
=25 дм  KK1 = 25 дм.
KK1 = 25 дм.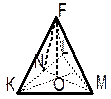
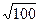 =10(м).
=10(м).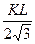 =
= 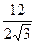 =
= 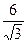 =2
=2 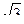 (м).
(м).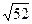 =
= 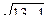 = 2
= 2 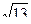 (м).
(м). АВС =900.
АВС =900.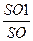 =
= 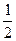
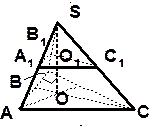
 = k2
= k2  А1В1С1/ S
А1В1С1/ S 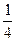 . S
. S 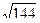 =12 (дм). S
=12 (дм). S  =54 (дм).
=54 (дм).


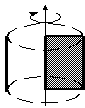
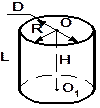
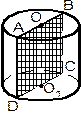
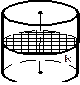
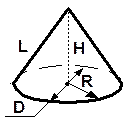


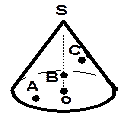
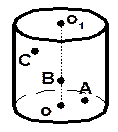
 см. Найдите площадь осевого сечения и площадь основания цилиндра.
см. Найдите площадь осевого сечения и площадь основания цилиндра.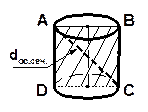
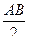 = 4
= 4 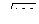 = 6
= 6 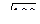 = 10(дм) Þ Rш. = 10дм.
= 10(дм) Þ Rш. = 10дм.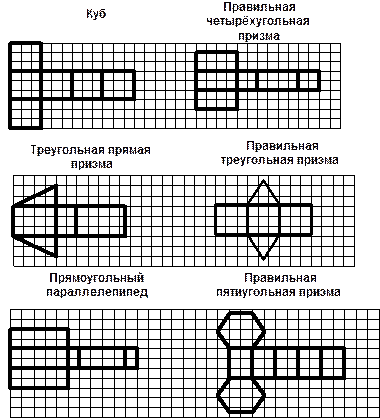
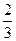 м3
м3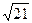 дм3
дм3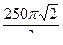
 )
)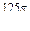
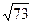 )
)