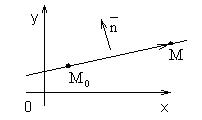
Рис. 1.5.15

Пусть прямая проходит через точку M₀(x₀, y₀).

Под нормальным вектором понимают ненулевой вектор, который перпендикулярен данной прямой. Обозначим его` .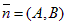

Возьмем на прямой произвольную точку M(x, y) и рассмотрим вектор 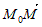. Его координаты равны 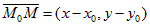. Вектор 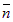`перпендикулярен вектору 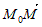. Из векторной алгебры известно, что скалярное произведение ортогоналльных векторов равно нулю. Следовательно, уравнение прямой по точке и нормальному вектору имеет вид:

Общее уравнение прямой имеет вид:

Коэффициенты А и В в уравнении определяют координаты нормального вектора: .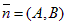

Рассмотрим общее уравнение прямой подробнее.

1) Если А = 0, то 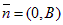, уравнение примет вид By + C = 0; y = – 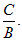Прямая параллельна оси Ox.

2) Если В = 0, то 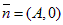, уравнение примет вид: Ax + C = 0, x = – 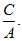Прямая параллельна оси Oy.

3) Если С = 0, то уравнение примет вид: Ax + By = 0, y = – 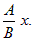Прямая проходит через начало координат и имеет угловой коэффициент k = –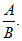

Из общего уравнения прямой, если В ≠ 0, можно найти угловой коэффициент k. Для этого выразим y из уравнения: Ax + By + C = 0: By = – Ax – C или
y = – –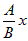

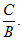
Угловой коэффициент прямой на плоскости:

k = –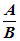

(1.5.5)

Пример. Прямая задана уравнением 3x – 4y +5 = 0. Найти координаты нормального вектора.

Решение: Координатами нормального вектора `n являются коэффициенты при x и y данного уравнения прямой. Имеем А = 3; В = –4.

Ответ: .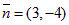

Пример. Составить уравнение прямой, проходящей через точку М(2, –1) и имеющей нормальный вектор .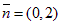

Решение: Применяем формулу (1.3.3). Имеем 0(x – 2) + 2(y + 1)= 0 Þ 2y + 2 = 0 Þ y + 1 = 0.

Ответ: y + 1 = 0.

Пример. Составить уравнение прямой, проходящей через точку М(0; 1) перпендикулярно вектору 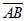, где А(–1; 2), В(1; –1).

Решение: Найдем координаты вектора 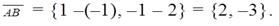Вектор 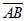является нормальным вектором искомой прямой. По формуле (1.3.3) имеем

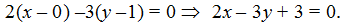
Ответ: 2x – 3y + 3 = 0.

Уравнение прямой по точке и направляющему вектору:

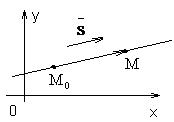
Рис. 1.5.16

Пусть прямая проходит через точку M₀(x₀, y₀).

Определение. Направляющим вектором 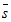данной прямой называется ненулевой вектор, параллельный этой прямой.

Пусть дан вектор 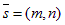. Возьмем на прямой произвольную точку M(x, y) и рассмотрим вектор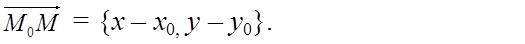

Векторы`s и 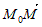коллинеарны, следовательно, их соответствующие координаты пропорциональны.

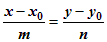
(1.5.6)

Полученное уравнение называется уравнением прямой по точке и направляющему вектору.

Пример. Прямая задана уравнением 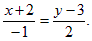Написать координаты направляющего вектора; найти координаты точки, лежащей на прямой; составить общее уравнение прямой.

Решение: Направляющий вектор 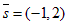. Точку M₀ мы получим, приравняв нулю числители данного уравнения: .

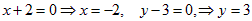Итак, M₀(−2; 3).

Общее уравнение прямой получим по свойству пропорций: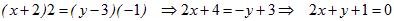

Ответ: 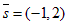, M₀ (−2; 3), 2x + y + 1 = 0.

Пример. Составить уравнение прямой по точке М(2, −5) и направляющему вектору .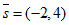

Решение: Применяем формулу (1.5.6). Имеем:

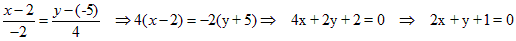
Ответ: 2x + y + 1 = 0.

Пример. Через точку С(−2, 1) провести прямую, параллельную вектору 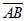, где А(2, −1), В(3, 4).

Решение: Вектор 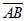можно взять за направляющий вектор данной прямой.

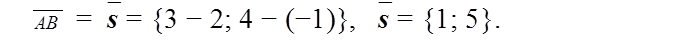
Применяем формулу (1.5.6). Имеем:

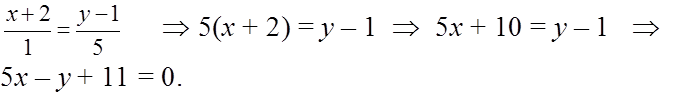
Ответ: 5x – y + 11 = 0.