Найдем векторные произведения ортов координатных осей: 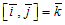, , 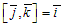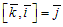(рис.10).

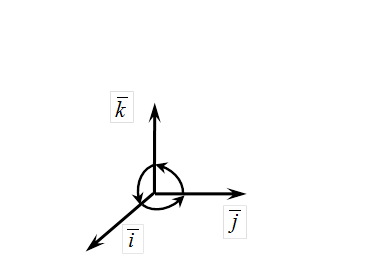
Рис.10

Пусть векторы ā и`b заданы своими координатами: ā = (x<sub>1</sub>, y<sub>1</sub>, z<sub>1</sub>), `b = (x₂, y₂, z₂).

Найдем .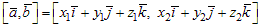

Используя распределительное и сочетательное свойства векторного произведения (свойства 4, 5), найденные векторные произведения ортов координатных осей окончательно векторное произведение запишется:

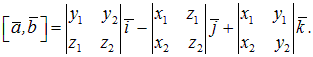
Для удобства вычисления координат вектора, являющегося векторным произведением, полученная сумма формально записывается в виде определителя третьего порядка, в первой строке которого стоят не числа, а координатные орты, во второй строке - координаты первого вектора ā, в третьей строке – координаты второго вектора`b

.

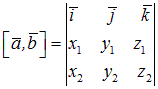Полученная выше сумма является разложением этого определителя по первой строке.

Тема 1.5. Аналитическая геометрия на плоскости.

1.5.1. Прямая на плоскости, различные виды уравнения прямой.

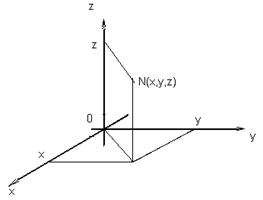
Под системой координат на плоскости или в пространстве понимают способ, позволяющий численно описать положение точки плоскости или пространства. Одной из таких систем является прямоугольная (декартова) система координат. Прямоугольная система координат задается взаимно перпендикулярными прямыми (рис. 1.5.1, рис.1.5.2), на каждой из которых выбрано положительное направление, и задан единичный отрезок. Эти прямые называются осями координат, точка их пересечения (точка O) – начало координат, Ox – ось абсцисс, Oy – ось ординат.

Рис.1.5.1	Рис.1.5.2

Линией l, определяемой уравнением F(x, y) = 0, называется геометрическое место точек плоскости Oxy, координаты которых удовлетворяют этому уравнению. Это означает, что координаты любой точки линии l удовлетворяют уравнению F(x, y) = 0, а координаты любой точки, не принадлежащей линии l, этому уравнению не удовлетворяют.

Уравнение линии дает возможность заменить изучение геометрических свойств линии исследованием ее уравнения.

Чтобы ответить на вопрос, лежит ли точка на линии l, достаточно знать координаты точки M и уравнение линии l.

Пример. Лежит ли точка M(5, 3) на окружности: x² + y² = 16?

Решение. Подставим значения x = 5, y = 3 в уравнение окружности: x² + y² ≠ 16. Точка M(5, 3) не лежит на данной окружности.

Пример. Лежит ли точка K(–2, 1) на линии 2x + y + 3 = 0?

Решение. Подставив x = –2, y = 1 в уравнение линии, получим: 2(–2 ) + 1 + 3 = 0. Точка K(–2, 1) лежит на данной линии.

Прямая y = kx + b

Простейшей из линий, изучаемых в геометрии, является прямая. Всякую прямую, не параллельную оси ординат, можно представить уравнением вида:

,где k есть тангенс угла α, образованного прямой с положительным направлением оси абсцисс Ox; k = tg α, M(0, b).

Величину k называют угловым коэффициентом, величину b – начальной ординатой.

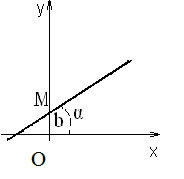
Рис.1.5.3	Рис. 1.5.4	Рис. 1.5.6

Если прямая параллельна оси Ox, то α = 0, k = tgα = 0 (см. рис. 1.5.7, 1.5.8). Уравнение горизонтальной прямой имеет вид:

y = b

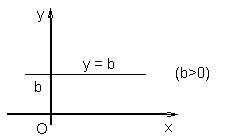
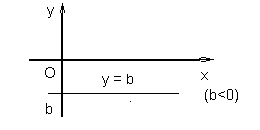
Рис. 1.5.7	Рис. 1.5.8

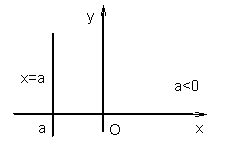
Если прямая параллельна оси Oy, то α = ^p/₂, а угловой коэффициент k = tg^p/₂ не существует (см. рис. 1.5.9, 1.5.10).

Уравнение вертикальной прямой имеет вид:

x = a,

где a – абсцисса точки, через которую проходит данная прямая (точки пересечения прямой с осью Ox).

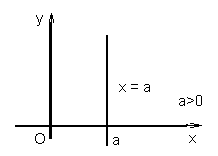
Рис. 1.5.9	Рис. 1.5.10

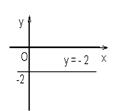
Рис. 1.5.11	Рис. 1.5.12	Рис. 1.5.13

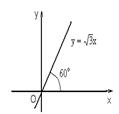
Пример. Какую прямую представляет уравнение y = 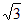x?

Решение. Данное уравнение задает прямую, у которой k = 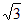; b = 0. Так как k = tg α = 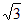, то α = 60º.

Поэтому данное уравнение представляет прямую, проходящую через начало координат (b = 0) и образующую с осью Ox угол 60º (рис. 1.5.11).

Пример. Написать уравнение прямой, параллельной оси Ox и имеющей начальную ординату b = –2.

Решение: По формуле y = b при b = –2 имеем y = –2. Итак, искомая прямая задается уравнением y = –2 (рис.1.5.12).

Ответ: y = –2.

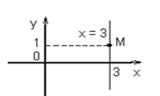
Пример. Написать уравнение прямой, параллельной оси Oy и проходящей через точку M(3, 1).

Решение: По формуле x = a при а = 3 имеем x = 3. Следовательно, искомая прямая задается уравнением x = 3 (рис.1.5.13).

Ответ: x = 3.