1) Если столбцы X1, X2,… Xk являются решениями однородной системы AX = 0, то их линейная комбинация c1X1 + c2X2 + … + + ckXk также является решением системы.
2) Если ранг матрицы однородной системы (7) меньше числа неизвестных (r = rg A < n), то система (7) имеет n – r линейно независимых решений.
Определение. Пусть rg A = r < n, тогда любая совокупность n – r линейно независимых решений однородной системы линейных уравнений (7) называется фундаментальной системой решений.
Теорема 2.4 (о структуре общего решения однородной системы линейных уравнений). Пусть X1, X2,… Xn – r – фундаментальная система решений однородной системы линейных уравнений, тогда общее решение системы (7) можно представить в следующем виде:
X = c1X1 + c2X2 + … + + cn – rXn – r
где c1, c2, … cn – r – произвольные постоянные.
Пример 2. Найти общее решение и фундаментальную систему решений однородной системы линейных уравнений:
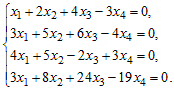
Приведем расширенную матрицу системы с помощью элементарных преобразований над строками к ступенчатому, а затем к упрощенному виду:
Получим систему уравнений, эквивалентную исходной:
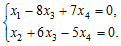
Переменные x1, x2 – базисные, x3, x4 – свободные. Выразив базисные переменные через свободные, получим общее решение:
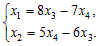
Найдем фундаментальную систему решений. Так как r = rgA = 2 и n = 4, n–r = 2, надо подобрать 2 линейно независимых решения. Подставим в общее решение стандартные наборы значений свободных переменных:
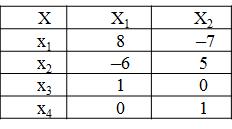
В результате получим фундаментальную систему решений:
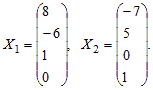
Запишем общее решение однородной системы по формуле (15):
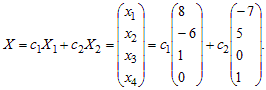
Тема 1.3. Векторная алгебра
1.3.1. Векторы: некоторые определения.
Из курса физики известно, что некоторые физические величины,например, температура, масса, плотность являются скалярными, другие величины, например, сила, скорость, ускорение, являются векторными.
Каждая скалярная величина характеризуется одним числом, которое выражает отношение этой величины к соответствующей единице измерения. Для характеристики векторной величины одного числа недостаточно, так как, кроме размерности, векторные величины обладают еще и направлением.
Для рассмотрения физических векторных величин применяются геометрические векторы.
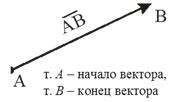
Рис. 1
Определение. Геометрическим вектором (или просто вектором), называется направленный отрезок.
Рис. 2
Векторы обозначаются либо двумя большими латинскими буквами, одна из которых – начало вектора, другая – конец вектора: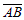 
, либо одной маленькой латинской буквой, над которой ставится черта: ā.
Начало вектора называется точкой приложения вектора.
Определение. Длиной вектора называется расстояние между началом и концом вектора.
Длина вектора называется модулем вектора и обозначается: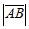 
, |ā| (очевидно, что |ā| ³ 0 для любого вектора ā).
Определение. Нулевым или нуль-вектором называется вектор, у которого начало и конец совпадают. Обозначение: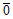 
( 
).
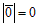Определение. Коллинеарными называются векторы, лежащие на одной прямой или параллельных прямых. Обозначение: ā ||`b.
Определение. Сонаправленными называются коллинеарные векторы, имеющие одинаковое направление. Обозначение: ā ↑↑`b.
Определение. Противоположно направленными называются коллинеарные векторы, имеющие противоположные направления. Обозначение: ā ↑↓`b.
|
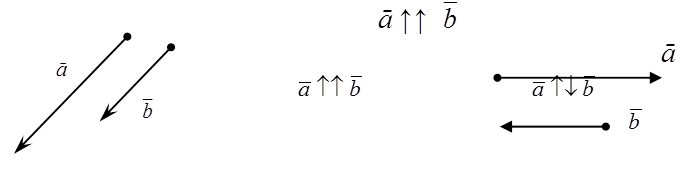
| Рис.3 |
Определение. Равными называются векторы, если они сонаправлены и имеют одинаковые длины.
Пример. Рассмотрим параллелограмм ABCD и векторы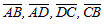 
, идущие по его сторонам (рис. 4).
|
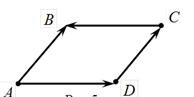
| Рис.4 |
Согласно данному определению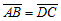 
, но 
.
|
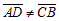| Рис.5 |
Из определения равенства двух векторов следует, что для каждого вектора его точка приложения может быть выбрана произвольно. Не различаются два вектора, получающиеся один из другого параллельным переносом (рис.6).
В соответствии с этим определением векторы, изучаемые в курсе векторной алгебры, называются свободными.
Определение. Компланарными называются векторы, лежащие в одной плоскости или параллельных плоскостях.
Отметим, что два вектора всегда компланарны, а три вектора могут быть компланарными, а могут и не быть компланарными.
1.3.2. Линейные операции над векторами.
Линейными операциями над векторами называются операции сложения векторов и умножения вектора на число.
Так как рассматриваются линейные операции не с числами, а с новыми объектами – направленными отрезками, – то сначала мы приведем определения этих операций.
Сложение векторов
|
| Рис.6 |
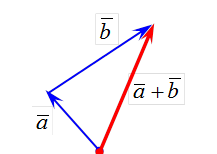
Определение. Суммой двух векторов ā и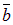 
называется вектор ā +`b, идущий из начала вектора ā в конец вектора `b при условии, что вектор`b приложен к концу
вектора ā (рис.7).
Это правило сложения векторов называют правилом треугольника.
Дата: 2018-12-21, просмотров: 261.
