1. Геометрический смысл модуля векторного произведения.

Пусть векторы ā и`b приведены к общему началу, тогда модуль векторного произведения равен площади параллелограмма, построенного на этих векторах как на сторонах (рис.5).

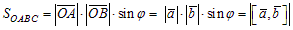
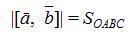
Рис.5

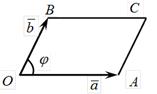
2. Равенство нулю векторного произведения. Для того, чтобы векторное произведение двух ненулевых векторов равнялось нулю необходимо и достаточно, чтобы эти векторы были коллинеарны.

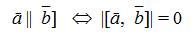
►Доказательство необходимости. Дано: [ā,`b] =`0. Докажем, что ā ||`b. По определению 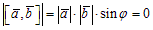, тогда sinj = 0, т.к. по условию 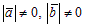. Значит, либо j = 0, либо j =p, поэтому ā ||`b. |[ā,`b]| = S_OABC.

Доказательство достаточности. Дано: ā ||`b. Доказать, что [ā,`b] =`0.

По условию ā ||`b, тогда либо j = 0, либо j = p. Значит, 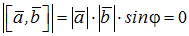, тогда и .◄

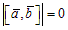Следствие. [ā, ā] =`0.

3. 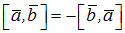– антипереместительный закон.

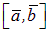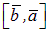►Доказательство. Длины векторов и равны, т. к. они равны площади параллелограмма, построенного на этих векторах, а направления этих векторов противоположны (рис.6).◄

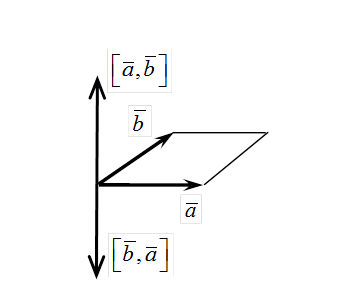
Рис. 6

4. 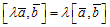– сочетательный закон (постоянный множитель можно выносить за знак векторного произведения).

Физический смысл векторного произведения

Заданный вектор силы` F приложен в точке B (рис. 9).

Определение. Моментом силы` F относительно какой-либо точки A называется векторное произведение вектора, идущего из точки A в точку приложения вектора силы (в точку B), на вектор силы` F.

.

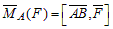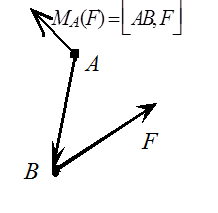
Рис.9

Вектор 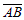, идущий из точки A в точку B, называется радиусом-вектором точки приложения силы.

Векторное произведение [ā,`b] можно рассматривать как момент силы, если первый сомножитель ā в векторном произведении принять за радиус-вектор точки приложения силы, а второй сомножитель`b – за вектор силы.

Вычисление векторного произведения в прямоугольной системе координат

Найдем векторные произведения ортов координатных осей: 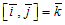, , 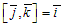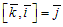(рис.10).

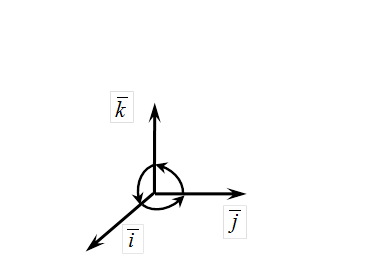
Рис.10

Пусть векторы ā и`b заданы своими координатами: ā = (x<sub>1</sub>, y<sub>1</sub>, z<sub>1</sub>), `b = (x₂, y₂, z₂).

Найдем .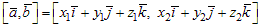

Используя распределительное и сочетательное свойства векторного произведения (свойства 4, 5), найденные векторные произведения ортов координатных осей окончательно векторное произведение запишется:

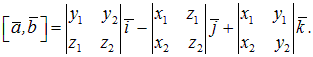
Для удобства вычисления координат вектора, являющегося векторным произведением, полученная сумма формально записывается в виде определителя третьего порядка, в первой строке которого стоят не числа, а координатные орты, во второй строке - координаты первого вектора ā, в третьей строке – координаты второго вектора`b

.

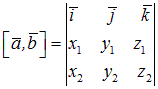Полученная выше сумма является разложением этого определителя по первой строке.

Векторное произведение векторов. Тройки векторов. Векторное произведение: определение, свойства, физический смысл. Вычисление векторного произведение в прямоугольной системе координат.