Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

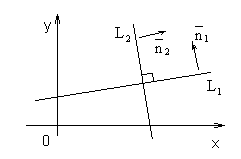
Рис. 1.5.27

Если две прямые l₁: y = k₁x + b₁ и l₂: y = k₂x + b₂. взаимно перпендикулярны, то угол между ними j = 90º, Так как tg 90º не существует, то это означает, что в формуле 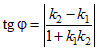знаменатель равен нулю, то есть 1 + k₁k₂ = 0. Отсюда

k 1 k 2 = –1 или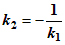

(1.5.13)

Это и есть условие перпендикулярности двух прямых.

 

Пример. Определить, какие из следующих пар прямых взаимно перпендикулярны:

a) 2x – y + 7 = 0 и x + 2y – 5 = 0

б) x + y – 3 = 0 и 2x + 3y + 7 = 0 .

Решение: а) По формуле (1.5.5) найдем угловые коэффициенты прямых:

k₁ = 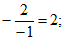k₂ = –¹/₂. Проверим условие (1.5.13) k₁·k₂ = 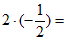–1. Условие выполнено, следовательно, прямые перпендикулярны.

б) Аналогично, 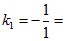–1; 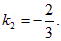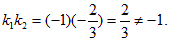Прямые не перпендикулярны.

Если перпендикулярные прямые заданы общими уравнениями, задачу можно решить другим способом. Из того, что прямые перпендикулярны, следует, что их нормальные векторы тоже перпендикулярны (верно и обратное утверждение).

Рассмотрим прямые l₁: 2x – y + 7 = 0 и l₂: x + 2y – 5 = 0.

Выпишем нормальные векторы этих прямых , .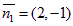

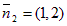Найдем скалярное произведение этих векторов: ( 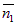, 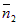) = 2·1 + (–1)·2 = 0. Из векторной алгебры известно, что если скалярное произведение векторов равно нулю, то эти векторы перпендикулярны: 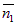^ 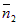. Следовательно, прямые l₁ и l₂ взаимно перпендикулярны: l₁ ^ l₂ .

1.5.3. Задачи для самостоятельного решения

 

1. Составить уравнение прямой, проходящей через точку A(–1; 2) параллельно прямой ВС, если В(3; –1) и С(–2; 4).

Указание: Уравнение прямой АК можно составить по точке А и направляющему вектору` s (см. пример 3 пункт 1.5.4). Направляющим вектором прямой ВС будет вектор 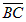= (–5; 5). Поэтому уравнение AK: 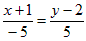или AK: x + y – 1 = 0.

Ответ: x + y – 1 = 0.

 

2. Через точку А(–3; –1) провести прямую, параллельную прямой x + 2y = 0.

Указание: Из общего уравнения прямой l₁: x + 2y = 0 находим угловой коэффициент k₁= –¹/₂ ( 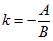(1.35.5)). Искомая прямая l₂||l₁, следовательно, (из условия параллельности двух прямых k₁ = k₂ (1.4.3)) имеем k₂ = –¹/₂. Cоставим уравнение искомой прямой l₂ по точке А(–3; –1) и угловому коэффициенту k₂ = –¹/₂ (см. пример 2, пункт 1.5.2)

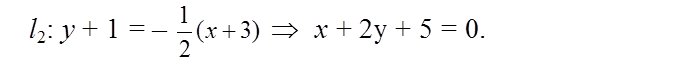
Ответ: x + 2y + 5 = 0.

 

3. Составить уравнение прямой, проходящей через точку А(1; –1) перпендикулярно прямой ВС, если В(2; 3) и С(–1; 4).

Указание: Искомая прямая перпендикулярна прямой ВС, следовательно, она перпендикулярна вектору 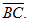Далее см. пример 3 пункт 1.5.3.

Ответ: 3x – y – 4 = 0.

 

4. Составить уравнение прямой, проходящей через точку D (1; –5) и перпендикулярной прямой 2x + 3y – 1 = 0.

Указание: Из общего уравнения прямой l₁: 2x + 3y –1 = 0 находим угловой коэффициент k₁ = –²/₃ ( 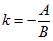(1.5.5)).

Прямая l₂ ^ l₁ Þ k₁·k₂ = –1 (1.5.13) или 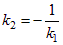(если k₁ ≠ 0), т.е. k₂ = ³/₂.

Составим уравнение искомой прямой l₂, проходящей через точку D(1; –5) и имеющей угловой коэффициент k₂ =³/₂. l₂: y + 5 =³/₂(x – 1). (см. пример 2 пункт 1.5.2).

Ответ: 3x – 2y – 13 = 0.

 

5. Даны вершины треугольника А(–1; 3), B(3; –2), C(5; 3). Составить уравнения сторон треугольника.

Указание: См. пример 3 пункт 1.5.5.

Ответ: AB: 5x + 4y – 7 = 0, BC: 5x – 2y – 19 = 0, AC: y – 3 = 0.

 

6. Даны вершины треугольника А(–3; 1), B(–3; –5), C(5; 3). Составить уравнение медианы, проведенной из вершины С.

Указание: См. пример 4 пункт 1.5.5.

Ответ: CM: 5x – 8y – 1 = 0.

 

7. Даны вершины треугольника A(1; –1), B(–2; 1) и C(3; 5). Составить уравнение перпендикуляра, опущенного из вершины А на медиану BE (см. рис. 1.5.28).

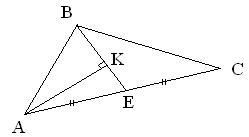
Рис. 1.5.28

Указание: Составим уравнение медианы ВЕ (см. 1.5.5) BE: x – 4y + 6 = 0. Уравнение перпендикуляра, опущенного из вершины А(1; –1) на медиану ВЕ составим как уравнение прямой, проходящей через точку А перпендикулярно прямой ВЕ . AK: 4x + y – 3 = 0.

Ответ: 4x + y – 3 = 0.

 

8. Даны вершины треугольника А(2; –1), B(3; 2), C(–2; –3). Составить уравнение высоты, проведенной из вершины С на сторону АВ.

Указание: Составим уравнение прямой АВ по двум точкам А(2;–1) и B(3; 2) (см. 1.5.5). AB: 3x – y – 7 = 0. Составим уравнение высоты СН как прямой, проходящей через точку C(–2; –3) и перпендикулярной прямой АВ

CH: x + 3y + 11 = 0.

Ответ: x + 3y + 11 = 0.

 

9. Даны вершины треугольника A(1; 2), B(–1; 3), C(–2; 1)(рис.46). Составить уравнение прямой, проходящей через вершину А параллельно противоположной стороне ВС (рис. 1.5.29).

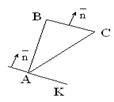
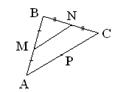
Рис. 1.5.29	Рис. 1.5.30

Указание: Составим уравнение прямой ВС по двум точкам B(–1; 3) и C(–2; 1) (формула 1.5.7). Получим: 2x – y + 5 = 0. Прямая АК параллельна противоположной стороне ВС, т.е. АК||ВС Þ k₁ = k₂ (1.5.12). Угловой коэффициент прямой ВС равен k₂ = 2 ( 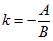(1.5.5)). Тогда угловой коэффициент прямой АК равен k₁ = 2. Составим уравнение искомой прямой по точке А и угловому коэффициенту k₁ . Получим AK: y – 2 = 2(x – 1) Þ

AK: 2x – y = 0.

Ответ: 2x – y = 0.

 

10. Даны середины сторон треугольника M(1; 2), N(5; –1) и

P(–4; 3) (рис.1.5.30). Составить уравнения его сторон.

Указание: MN – средняя линия треугольника АВС. Из курса геометрии известно, что MN параллельна стороне АС. Уравнение прямой АС находим как уравнение прямой, проходящей через точку P(–4; 3) и параллельной прямой MN.

AC: 3x + 4y = 0.

Аналогично составляем уравнения сторон AB и BC:

AB: 4x + 9y – 22 = 0; BC: x + 5y = 0.

Ответ: AB: 4x + 9y – 22 = 0; BC: x + 5y = 0; AC: 3x + 4y = 0.

 

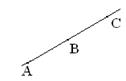
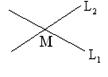
11. Проверить, лежат ли на одной прямой три данные точки(рис.1.5.31):

а) A(–2; 0), B(6; 4), C(4; 3);

б) M(1; –3), N(2; 4), P(3; –1).

Рис. 1.5.31	Рис. 1.5.32

Указание: Составим уравнение прямой по любым двум данным точкам. Уравнение прямой, проходящей через точки A(–2; 0) и B(6; 4) будет иметь вид: AB: x – 2y + 2 = 0 (см.1.5.5). Проверим, что точка С(4; 3) лежит на прямой АВ, т.е. что при подстановке координат точки С в уравнение x – 2y + 2 = 0 должно получиться тождество: 4 – 2·3 + 2 = 0 или 0 = 0.

Таким образом, точка С лежит на прямой АВ, т.е. три данные точки А, В, С лежат на одной прямой.

Ответ: а) лежат; б) не лежат.

 

12. Показать, что прямые 3x – 2y + 1 = 0 и 2x + 5y – 12 = 0 пересекаются; найти координаты точки пересечения прямых (рис.1.5.32).

Указание: Прямые пересекаются, если система

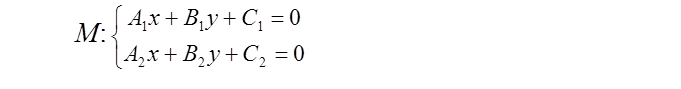
имеет единственное решение, это решение будет являться координатами точки пересечения прямых.

Систему можно решить исключением неизвестных или, используя формулы Крамера:

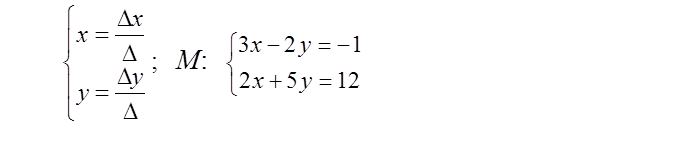
Найдем определители D, D_x ,D_y .

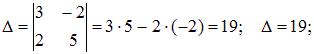Если D ≠ 0, то система имеет единственное решение, т.е. прямые пересекаются.

;

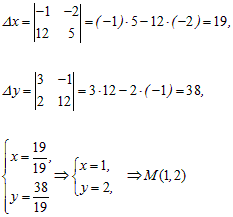Ответ: Прямые пересекаются в точке М(1; 2).

 

13. Через точку пересечения прямых 2x – y – 5 =0 и 3x + 2y + 3 = 0 провести прямую, перпендикулярную прямой 5x + 3y – 1 =0.

Указание: Точку пересечения двух прямых l₁ и l₂ найдем, решив систему :

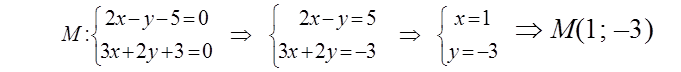
Составим уравнение искомой прямой l₄, проходящей через точку М(1; –3) и перпендикулярной прямой l₃: 5x + 3y – 1 = 0.

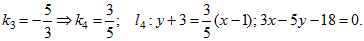
Ответ: 3x – 5y – 18 = 0.

 

14. Через точку пересечения прямых 5x + y – 9 = 0 и 3x – 2y – 8 = 0 провести прямую, параллельную прямой 2x – 3y + 7 = 0.

Указание: По условию l₁: 5x + y – 9 = 0 и l₂: 3x – 2y – 8 = 0. Точку М – точку пересечения прямых l₁ и l₂ найдем, решая систему уравнений 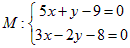(см. задачу 12) Þ М(2; –1).

Составим уравнение прямой l₄, проходящей через точку М(2; –1) и параллельной прямой l₃: 2x – 3y + 7 = 0 (см. решение задачи 2 пункт 1.7) Þ l₄: 2x – 3y – 7 = 0.

Ответ: 2x – 3y – 7 = 0.

 

15. Через точку пересечения прямых 5x + 2y + 1 = 0 и x – y + 3 = 0 провести прямую, параллельную оси Oy (рис.50).

Указание: Точку пересечения прямых l₁: 5x + 2y + 1 = 0 и l₂: x – y + 3 = 0 найдем, решив систему (см. задачу 12)

Рис.1.5.33

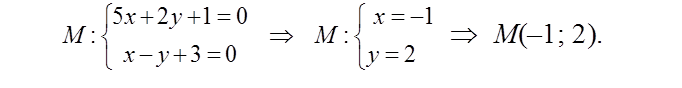
Составим уравнение прямой l₃, проходящей через точку и параллельной оси Oy. Направляющим вектором оси Oy является вектор ` j = (0; 1) и направляющим вектором искомой прямой l<sub>3</sub> будет вектор` s = (0; 1), т.к. прямая l₃ || Oy.

Составим уравнение прямой l₃, используя формулу (1.5.6):

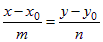– уравнение прямой по точке и направляющему вектору.

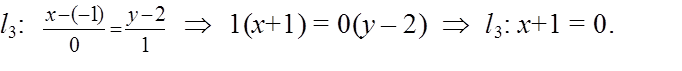
Уравнение прямой l₃: можно найти и по-другому (решить самостоятельно).

Ответ: x + 1 = 0.

 

16. Составить уравнение перпендикуляра, опущенного из точки С(3; 4) на прямую, проходящую через две точки А(2; –1) и B(0; 1).

Указание: Чтобы составить уравнение перпендикуляра, опущенного из точки С на прямую АВ, надо составить уравнение прямой, проходящей через точку С(3; 4) и перпендикулярной прямой АВ.

Ответ: x – y + 1 = 0.

 

17. Найти проекцию точки N(1; –1) на прямую x + 2y – 3 = 0 (рис.1.5.34).

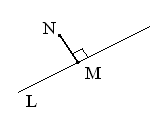
Рис.1.5.34

Указание: Проекцией точки N на прямую l: x + 2y – 3 = 0 будет точка М – точка пересечения прямой l и прямой, проходящей через данную точку N и перпендикулярной к прямой l. Составим уравнение прямой MN ^ l (задачу 4). П l: x + 2y – 3 = 0 Þ k₁ = –¹/₂;

Так как MN ^ l , то k₁·k₁ = –1 Þ k₂ = 2;

MN: y – y₀ = k(x – x₀), где N(1; –1) и k₂ = 2;

MN: y – (–1) = 2(x – 1) Þ MN: 2x – y – 3 = 0.

Найдем точку М как точку пересечения прямых l и MN, решив систему уравнений.

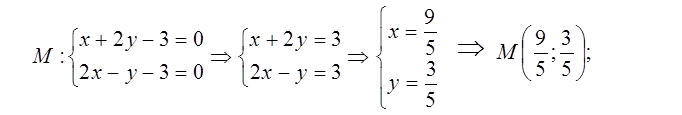
(см. задачу 12).

Проекцией точки N на прямую x + 2y – 3 = 0 является точка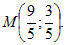

Ответ: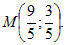

18. Найти проекцию точки А(–1; 3) на прямую ВС, если В(2; 2) и С(–1; –1).

Указание: Составим уравнение прямой ВС по двум точкам В(2; 2) и C(–1; –1) (см. пример 1 пункт 1.3.5). BC: x – y = 0.

Найдем проекцию точки A(–1; 3) на прямую ВС (см. задачу 17).

Ответ: D (1; 1).

 

19. Найти точку симметричную точке М(3; –3) относительно прямой x – y – 12 = 0 (см. рис 1.5.35).

Указание: Составим уравнение прямой MN, проходящей через точку M(3; –3) и перпендикулярной прямой l: x – y – 12 = 0 (см. решение задачи 4 ).

MN: x + y = 0.

Найдем точку пересечения прямой MN и прямой l :

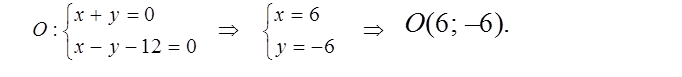
Точка О – середина отрезка MN и ее координаты находятся по формулам (1.2.2)

Пусть M(x₁, y₁) и N(x₂, y₂), а по условию x₁ = 3, y₁ = –3; x₀ = 6, y₀ = –6; выполним подстановку и найдем координаты точки N.

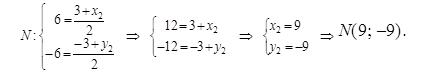
Ответ: N(9; –9).

Рис.1.5.35	Рис.1.5.36

 

20. При каком λ прямые 2x +3y – 5 = 0 и 3x + λy – 2 = 0 будут параллельны (решить двумя способами) (см. рис.1.5.36)?

Указание: Найдем угловые коэффициенты прямых l₁: 2x +3y –5 =0 и l₂: 3x + λy – 2 = 0. k₁ = –²/₃, k₂ = –³/_λ ( 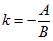(1.5.5)).

Так как l₁ || l₂, то k₁ = k₂ :

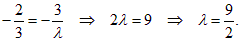
Задачу можно решить и другим способом. Найдем координаты нормальных векторов прямых l₁ и l₂: ` n<sub>1</sub> = (2; 3) и` n₂ = (3; λ). Прямые l₁ и l₂ параллельны, следовательно, их векторы нормали коллинеарны, а координаты этих векторов пропорциональны.

 

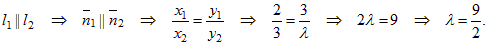
Ответ: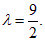

 

21. При каком значении α прямые 3x – 5y +3 = 0 и αx + y + 3 = 0 будут перпендикулярны (решить двумя способами)?

Указание: Прямые l₁: 3x – 5y +3 = 0 и l₂: αx + y + 3 = 0 перпендикулярны (рис.54), l₁ ^ l₂ Þ k₁·k₂ = –1.

 

Рис.1.5.37

Угловые коэффициенты: k₁ = ³/₅ и k₂ = –^α/₁ ( 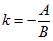(1.5.5)) и

найдем α: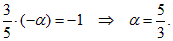

Задачу можно решить и другим способом. Найдем координаты нормальных векторов прямых l₁ и l₂: `n₁ = (3; –5) и n₂ = (α; 1) (1.5.4).

Так как l₁ ^ l₂, то и `n<sub>1</sub> ^ `n₂ Þ (`n<sub>1</sub>,`n₂) = 0 (скалярное произведение двух взаимно перпендикулярных векторов равно нулю). Найдем скалярное произведение

нормальных векторов в координатной форме и приравняем его к нулю.

3·α + (–5)·1 = 0 Þ α = ⁵/₃.

Ответ: α = ⁵/₃.

 

22. Найти угол между двумя прямыми x – 2y – 3 = 0 и x – y + 5 = 0.

Ответ: tgα = ¹/₃ или α = arctg ¹/₃ .

 

23. При каком А угол между прямыми Ax – y +3 = 0 и 2x + y – 1 =0 будет равен 45º?

Указание: l₁: Ax – y +3 = 0; l₂: 2x + y – 1 = 0. Угол между двумя прямыми l₁ и l₂ находится по формуле

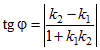
(1.5.2)

Угловые коэффициенты прямых l₁ и l₂ будут равны k₁ = A и k₂ = –2 ( k = – (1.5.5)), а j = 45º. Выполним подстановку в формулу и найдем А:

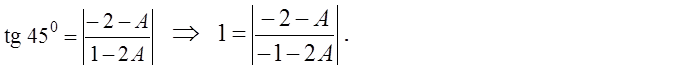
Раскрывая модуль, получим два уравнения. Решение обоих уравнений является решением задачи.

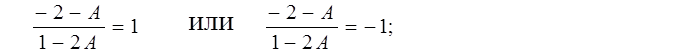
–2 – A = 1 – 2A или –2 – A = –1 + 2A; A = 3 или A = –¹/₃.

Ответ: A = 3 или A = –¹/₃.

 

24. Дана прямая 5x + y – 4 = 0. Через точку M₀(1; –2) провести прямую, наклоненную к данной прямой под углом 45º (рис.1.5.38).

Рис.1.5.38

Указание: Из общего уравнения прямой l₁: 5x + y – 4 = 0 найдем угловой коэффициент k₁ = –5 (k = – 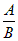(1.5.5)). Угловой коэффициент искомой прямой k₂ найдем из условия, что угол между прямыми l₁ и l₂ – равен 45º.

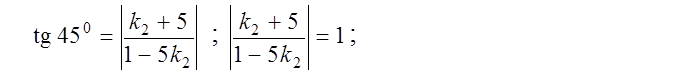
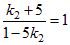или ;

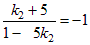k₂ + 5 = 1 – 5k₂ или k₂ + 5 = –1 + 5k₂ ;

k₂ = –²/₃ или k₂ = ³/₂ .

Составим уравнение искомой прямой по точке M₀(1; –2) и угловому коэффициенту k₂ = –²/₃ (или k₂ = ³/₂), используя формулу (1.5.2)

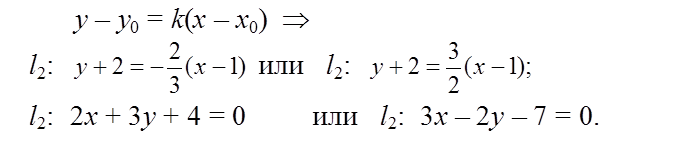
Ответ: 2x + 3y + 4 = 0 или 3x – 2y – 7 = 0.

 

Рис.1.5.39	Рис.1.5.40

 

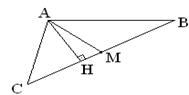
25. Определить угол между высотой и медианой треугольника АВС, проведенными из вершины А, если А(1; –1), B(–2; 1), C(2; 5)(рис.1.5.39).

Указание: Составим уравнение медианы АМ (см. пример 4).

AM: 4x + y – 3 = 0. Составим уравнение высоты AH (см. решение задачи 8 ).

AH: x + y = 0. Из общих уравнений прямых АМ и АН найдем угловые коэффициенты k₁ = –4 и k₂ = –1. Угол между прямыми АМ и АН найдем по формуле (1.5.2)

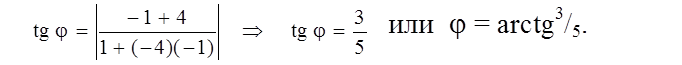
Ответ: tgj = ³/₅ или j = arctg³/₅.

 

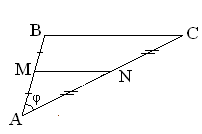
26. В треугольнике АВС известны координаты вершин А(–2; –2), B(1; 2) и C(3; –3). Найти угол ВАС и составить уравнение средней линии треугольника, лежащей против вершины В(рис.1.5.40).

Указание: Составим уравнения сторон АВ и АС (см. пример 3 )

AB: 4x – 3y + 2 = 0 и AC: x + 5y + 12 = 0. Найдем угол ВАС – угол между прямыми АВ и АС (см. пример 2).

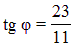или 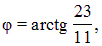где угол j равен углу ВАС. Составим уравнение средней линии MN. Так как точка М – середина отрезка АВ, а точка N – середина отрезка АС, то координаты точек М и N найдем по (1.2.2): M(–¹/₂, 0) и N(¹/₂, –⁵/₂). Составим уравнение средней линии MN по двум точкам (см. пример 1 пункт 1.3.5). MN: 10x + 4y +5 = 0.

Ответ: 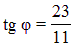или 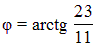и MN: 10x + 4y + 5 = 0.

 

 

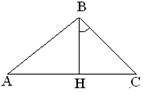
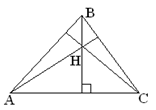
27. В треугольнике АВС известны координаты вершин A(1; –3), B(0; –1) и C(3; 3). Составить уравнение высоты и определить острый угол между высотой BH и стороной ВС.(см. рис.1.5.41)

Рис.1.5.41	Рис.1.5.42

Указание: Составим уравнение стороны ВС (см. пример 4)

BC: 4x – 3y – 3 = 0 k₁ = ⁴/₃ . Составим уравнение стороны AС: 3x – y – 6 = 0, k_AC = 3, Þ k_BH = –¹/₃. Составим уравнение высоты BH (см. задачу 8)

BH: x + 3y + 3 = 0.

Найдем угол HBC:

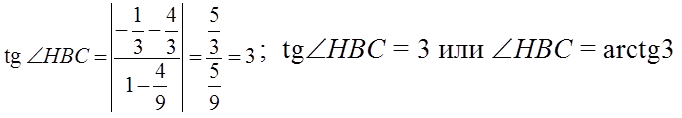
Ответ: BH: x + 3y + 3 = 0, ÐHBC = arctg3.

 

28. В треугольнике АВС известны координаты вершин А(4; 8), B(–3; 4) и C(–4; –1). Найти угол между сторонами АВ и АC. Составить уравнение средней линии, параллельной ВС.

Ответ: 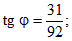MN: 10x – 2y + 7 = 0.

 

29. Даны вершины треугольника A(–2; 1), B(3; –4) и точка Н(5; –1) – точка пересечения высот. Составить уравнения его сторон (рис.1.5.42).

Указание: Составим уравнение прямой АВ как уравнение прямой, проходящей через две точки A(–2;1) и B(3; –4) (см. пример 3). AB: x + y + 1 = 0.

Уравнение стороны ВС составим как уравнение прямой, проходящей через точку B(3; –4) и перпендикулярной прямой АН (см. задачу 4).

Уравнение прямой АН составим, зная координаты двух точек А(–2; 1) и

Н(5; –1) AH: 2x + 7y – 3 = 0, тогда BC: 7x – 2y – 29 = 0. Аналогично находится уравнение прямой AC: 2x + 3y + 1 = 0.

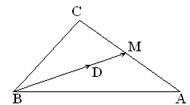
Рис.1.5.43

Ответ: AB: x + y + 1 = 0; BC: 7x – 2y – 29 = 0; AC: 2x + 3y + 1 = 0.

 

30. Найти координаты центра тяжести треугольника АВС, длину и уравнение медианы ВМ, если А(5; 6), B(–3; –1) и C(–3; –2) (рис.1.5.43).

Указание: Известно, что центр тяжести такой пластины находится в точке пересечения медиан D треугольника АВС. Для определения точки D учтем то, что она делит любую медиану, например ВМ, в отношении λ = 2, так как λ = 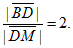Если координаты вершин A(x₁, y₁), B(x₂, y₂) и C(x₃, y₃), то координаты точки M(x_M, y_M) находим из условия, что она делит отрезок АС пополам, 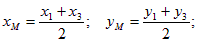а затем получим координаты точки D.

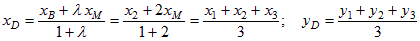
Согласно полученным формулам находим координаты центра тяжести – точки D.

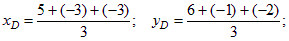
x_D = –¹/₃, y_D = 1; т.е. D(–¹/₃; 1).

Составим уравнение медианы ВМ, зная координаты точки В(–3; –1), а координаты точки М определим по формулам:

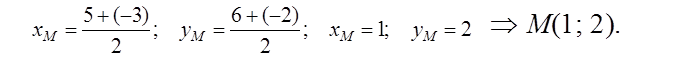
BM: 3x – 4y + 5 = 0. Длину медианы найдем, используя формулу расстояния между двумя точками В(–3; –1) и M(1; 2).

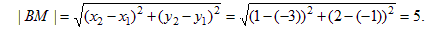
Ответ: D(–¹/₃; 1), BM: 3x – 4y + 5 = 0. | BM | = 5.

 

31. Определить расстояние от точки М до прямой 3x – 4y + 6 = 0,

если М(1; 2).

Ответ: d = ¹/₅.

 

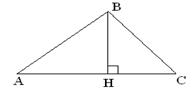
32. Даны стороны треугольника АВ: x + 3y – 7 =0, BC: 4x – y –2 =0, AC: 6x + 8y –35 =0. Найти длину высоты, проведенной из вершины В (рис.1.5.44).

Указание: Определяем координаты точки В как точки пересечения двух прямых. Длина высоты ВН находится как расстояние от точки В до прямой АС.

Ответ: BH = 1,3.

Рис.1.5.44	Рис.1.5.45

 

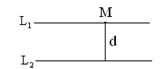
33. Определить расстояние между двумя прямыми 3x + 4y + 8 = 0 и 6x + 8y – 2 = 0 (рис.1.5.45).

Указание: Эти прямые параллельны, так как k₁ = –³/₄, k₂ = –⁶/₈= –³/₄ (угловые коэффициенты вычисляем по формуле 1.5.5).

Получаем k₁ = k₂ Þ l₁ || l₂ .

Найдем расстояние от любой точки М, лежащей на прямой l₁, до прямой l₂ – это и будет расстояние между двумя прямыми.

На прямой l₁ выберем точку М с абсциссой x = 0, тогда из уравнения l₁ найдем y = –2. Следовательно, точка М(0; –2). Расстояние от М(0; –2) до прямой l₂: 6x + 8y – 2 = 0 будет равно d = 1,8, так как

.

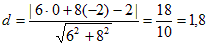Ответ: d = 1,8.

Тема 1.6. Аналитическая геометрия в пространстве.

1.6.1. Плоскость: способы задания, условия взаимного расположения плоскостей

Основные определения

Рассмотрим в трехмерном эвклидовом пространстве E³прямоугольную систему координат Oxyz.

Уравнением поверхности называется такое уравнение F(x, y, z) = 0, которому удовлетворяют координаты каждой точки, лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на поверхности.

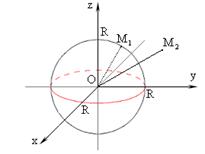
Рис.1.6.1

Например, сфера – это геометрическое место точек, равноудаленных от некоторой точки, называемой центром сферы. Так все точки, удовлетворяющие уравнению x² + y² + z² = R², лежат на сфере радиуса R с центром в точке О(0; 0; 0) (рис.1.6.1.). Координаты любой точки, не лежащей на данной сфере, не удовлетворяют этому уравнению.

Линию в пространстве можно рассматривать как линию пересечения двух поверхностей. Так на рисунке 1.6.1 пересечением сферы с плоскостью Oxy является окружность радиуса Rс центром в точке О.

Простейшей поверхностью является плоскость, простейшей линией в пространстве является прямая.

 

Плоскость: способы задания