1) 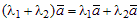(распределительное свойство векторного сомножителя относительно суммы чисел).

Докажите это свойство самостоятельно, используя определения линейных операций над векторами, рассмотрев два случая: l₁ и l₂ имеют одинаковые знаки, l₁ и l₂ имеют различные знаки.

2) 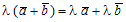(распределительное свойство числового сомножителя относительно суммы векторов).

3) 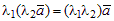(сочетательное свойство числового множителя).

Разность двух векторов.

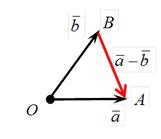
Рис.10

Определение. Разностью двух векторов ā и`b называется вектор ā –`b, который в сумме с вектором`b дает вектор ā (рис.10).

Рассмотрим векторы ā и`b. Приведем их к общему началу O. Обозначим: 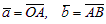. Тогда, согласно данному определению: .

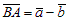Разность векторов ā и`b можно рассматривать как сумму вектора ā и вектора (–`b), противоположного` 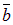, т.е. как ā +( –`b).

Рис.11 ,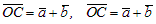

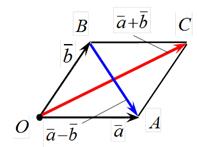
Замечание. Если векторы ā и 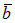приведены к общему началу и на них, как на сторонах, построен параллелограмм (рис. 11), то та из диагоналей этого параллелограмма, которая

выходит из их общего начала, является суммой векторов: 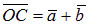, а вторая диагональ 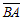является разностью векторов: .

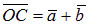Определение. Единичным вектором называется вектор, длина которого равна единице, т.е. |ā| = 1.

Определение. Орт вектора ā – это единичный вектор, сонаправленный с вектором ā.

Орт вектора ā обозначается ā⁰ (ā⁰ ↑↑ ā, |ā⁰| = 1).

Согласно этому определению: ā = |ā| ā⁰ или .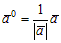

1.3.3. Необходимое и достаточное условие коллинеарности двух векторов.

Теорема. Для того, чтобы два вектора ā и`b были коллинеарны, необходимо и достаточно, чтобы один из них мог быть представлен в виде произведения некоторого числа на другой вектор, т. е. 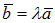(или ).

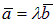В этой теореме мы должны доказать два признака; один из них является необходимым для данного утверждения, а другой достаточным.

Такая формулировка теоремы встречается нам впервые. Уточним, в каком случае признак называется необходимым для данного утверждения, а в каком - достаточным.

Пусть имеется некоторое утверждение и какой-либо признак для проверки справедливости этого утверждения.

Если из справедливости данного утверждения следует выполнение признака, то такой признак называется необходимым для данного утверждения.

Если же наоборот – из выполнения признака следует справедливость данного утверждения, то такой признак называется достаточным для данного утверждения.

Признак может быть только необходимым, или только достаточным, или одновременно и достаточным, и необходимым.

Доказательство теоремы разобьем на две части.

i) Докажем необходимость. Если один из векторов, например, `b =`0, то `b = 0·ā = lā (при l = 0) и теорема доказана).

Пусть векторы ā и `b коллинеарны, ā ¹ 0 и`b ¹ 0. Докажем, что существует действительное число l такое, что `b = lā.

Рассмотрим орты векторов ā и `b: .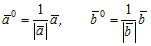

а) Если векторы ā и`b сонаправлены, то ā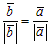<sup>0</sup> =`b ⁰, т. е. или 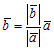. Обозначив 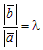, получим `b = lā. Заметим, что в этом случае l > 0.

б) Если векторы ā и`b направлены противоположно, то ā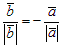<sup>0</sup> = –`b ⁰, т. е. или 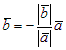. Обозначив 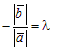, получим `b = lā.

Заметим, что в этом случае l < 0. Таким образом, если векторы ā и`b коллинеарны, то`b = lā.

ii) Докажем достаточность. Пусть даны два вектора ā и`b, и известно, что существует число l такое, что`b = lā. Надо доказать, что ā ||`b.

Доказательство этого утверждения немедленно следует из определения умножения вектора на число.