Напомним, что любые два вектора можно считать лежащими в одной плоскости.

Разложить вектор`с на плоскости по двум неколлинеарным векторам ā и `b – значит представить вектор`с в виде cуммы 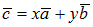, где x и y – некоторые числа.

Теорема. Если ā и`b два неколлинеарных вектора, лежащих в одной плоскости, то любой вектор`с, лежащий с векторами ā и`b и в одной плоскости, можно разложить по векторам ā и`b, т. е. представить в виде 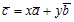, где x, y – некоторые числа, и такое разложение единственно.

Рис.12

Доказательство.

1) Докажем возможность (существование) такого разложения.

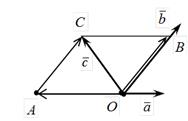
Приведем векторы ā и `b к общему началу O. Рассмотрим произвольный вектор`с, лежащий в этой плоскости. Приложим его к точке O. (рис. 12).

Построим параллелограмм OABC, стороны которого параллельны векторам ā и`b, а вектор`с является диагональю этого параллелограмма.

По правилу параллелограмма: 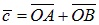. Вектор ,
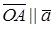тогда по необходимому условию коллинеарности: 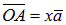. Вектор 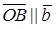, тогда по необходимому условию коллинеарности: .

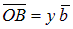Получаем: 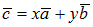, где x, y – некоторые числа, и возможность разложения вектора`c по векторам ā и` 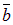доказана.

2) Докажем единственность разложения. Покажем, что числа x и y для каждого вектора`с определяются единственным образом.

Доказательство проводится методом «от противного».

Допустим, что существуют числа x₁ и y₁ такие, что 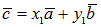, причем справедливо хотя бы одно из неравенств x ¹ x₁, y ¹ y₁. Тогда 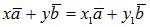или .

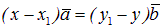Предположим, что x ¹ x₁, тогда .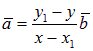

Если обозначить 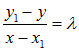, то 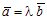, значит векторы ā и`b коллинеарны в силу достаточного условия коллинеарности векторов, что противоречит условию теоремы (ā и`b не коллинеарны).

Значит предположение о существовании другого разложения вектора`с по векторам ā и`b неверно, следовательно, такое разложение единственно.

В связи с этой теоремой дадим следующее определение.

Определение. Базисом на плоскости называются любые два неколлинеарных вектора.

Используя понятие базиса, доказанную теорему можно сформулировать следующим образом.

В доказанной выше теореме базисными векторами являются векторы ā и`b.

1.3.5. Разложение вектора в пространстве по трем некомпланарным векторам

Пусть ā,`b,`с – три некомпланарных вектора.

Разложить вектор`d по векторам ā,`b и`с – значит представить вектор`d в виде cуммы 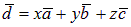, где x, y и z – некоторые числа.

Теорема. Любой вектор`d в пространстве можно разложить по трем некомпланарным векторам ā,`b и`с, и такое разложение единственно.

Доказательство этой теоремы аналогично доказательству предыдущей теоремы, только в данном случае нужно построить параллелепипед, ребра которого параллельны векторам ā,`bи`с, а вектор`d является диагональю этого параллелепипеда.

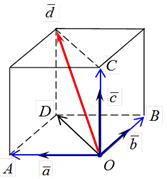
Рис.13

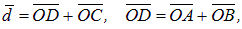, т.е. 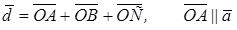, тогда по необходимому условию коллинеарности: ,

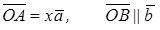тогда по необходимому условию коллинеарности: ,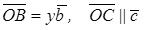

тогда по необходимому условию коллинеарности: .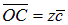

Таким образом получается разложение: 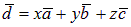, где x, y и z – некоторые числа (рис.13).

Единственность этого разложения доказывается методом от противного, аналогично тому, как это сделано в предыдущей теореме. Предлагается сделать это самостоятельно.

Определение. Базисом в пространстве называются любые три некомпланарных вектора.

Доказанную теорему можно сформулировать следующим образом.

В приведенной теореме базисными векторами являются векторы ā,`b и`с.

Замечание. Базис на плоскости и в пространстве можно выбрать бесконечным числом способов.

1.4.1. Проекция вектора на ось

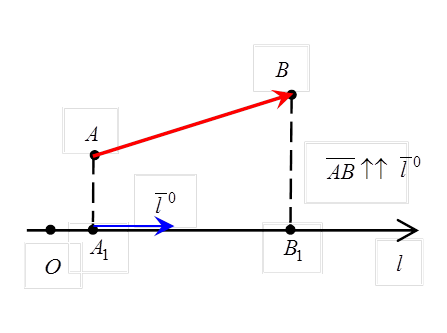
Задана некоторая ось l (прямая с выбранным на ней направлением, началом отсчета и масштабом измерения) и вектор .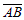

Рис.1	Рис.2

На рис.1, 2 вектор `l⁰ – орт оси l, т.е. единичный вектор, сонаправленный с осью.

Из точек A и B опускаются перпендикуляры на ось l, через точку A₁ обозначим проекцию точки A (начала вектора), через B – проекцию точки B (конца вектора ).

Определение. Вектор 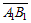, идущий из проекции начала в проекцию конца вектора 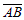называется компонентой (или составляющей) вектора 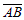по оси l.

Обозначение: .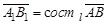

Определение. Проекцией вектора на ось называется число, равное модулю компоненты этого вектора, взятое со знаком плюс, если направление компоненты совпадает с направлением оси, и со знаком минус, если направление компоненты противоположно направлению оси.

Обозначается проекция вектора 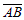на ось : .

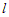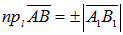На рис. 1: 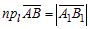, на рис. 2: .

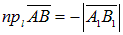Если 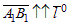(направление компоненты совпадает с направлением оси), то 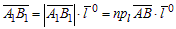(рис. 1).

Если 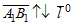(направление компоненты противоположно направлению оси), то 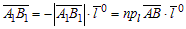(рис. 2).

Вывод: компонента вектора по оси всегда равна произведению орта оси на проекцию вектора эту ось:

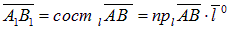
Определение. Углом наклона вектора к оси называется наименьший из углов, которые образует вектор с положительным направлением оси (рис.3).

Рис.3

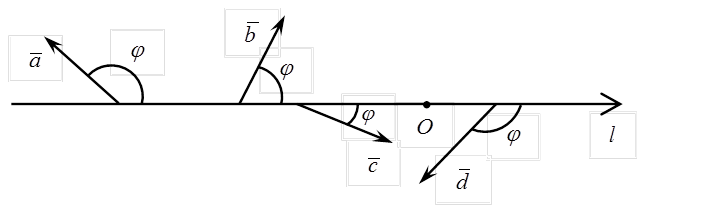
На приведенных рисунках угол наклона вектора к оси обозначен буквой j (очевидно, что 0 ≤ j ≤ p).

Свойства проекций

Доказательство. Рассмотрим отдельно случаи: а) угол наклона вектора к оси острый, б) угол наклона вектора к оси тупой, в) вектор перпендикулярен к оси.

Рис.4

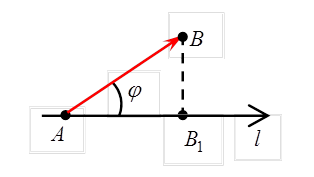
а) Пусть 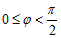(рис.4), тогда из DABB₁: .

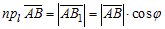Рис.5

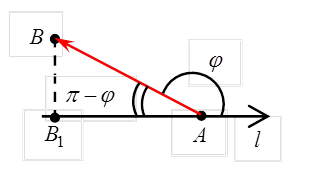
б) Пусть 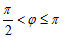(рис 5), тогда из DABB₁:

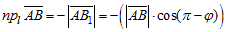, т.е.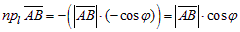

Рис.6

в) Пусть 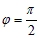(рис.6), тогда .

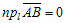Окончательно для любого случая

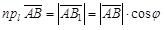
Замечание. Это свойство с помощью обычной индукции легко распространить на сумму любого конечного числа векторов.