Системой m линейных уравнений с n неизвестными называется система уравнений вида:
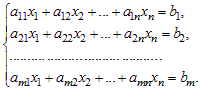
| (1) |
Числа aij (i = 1, 2,… m; j = 1, 2,… n) называются коэффициентами системы, x1, x2,… xn – неизвестными, b1, b2,… bm – свободными членами.
Решением системы (1) называется совокупность чисел c1, c2,… cn, которые, будучи подставлены вместо неизвестных в систему, обращают уравнения системы в тождества.
Система называется квадратной, если число уравнений m равно числу неизвестных n .
Система называется совместной, если она имеет хотя бы одно решение. Система называется несовместной, если она не имеет решений.
Рассмотрим квадратную систему n линейных уравнений с n неизвестными:
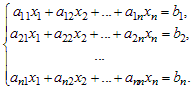
| (2) |
Введем матрицу системы 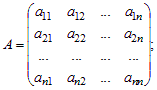
и матрицы-столбцы 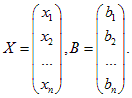
В силу определения умножения матриц и равенства матриц, система n линейных уравнений с n неизвестными (2) равносильна одному матричному уравнению
| AX = B | (3) |
Уравнение (3) называют матричной записью системы (2).
Теорема 2.1. Рассмотрим квадратную систему линейных уравнений (2), записанную в матричном виде (3): AX = B. Пусть матрица A системы невырожденная, т.е. det A ≠ 0. Тогда в силу теоремы 1.2 (главы 1) уравнение (3) (а, значит, и система (2)) имеет единственное решение:
| X = A–1B |
1.2.2. Решение квадратной системы линейных уравнений по формулам Крамера
Главным определителем системы линейных уравнений (2) называется определитель матрицы A:
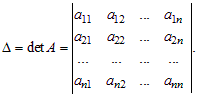
Теорема 2.2. Пусть главный определитель Δ системы (2) отличен от 0, тогда система имеет единственное решение, которое находится по формулам Крамера:
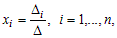
где Δi – определитель, полученный из главного определителя Δ заменой i-того столбца столбцом свободных членов, т.е.
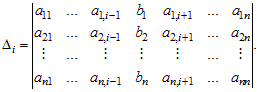
Пример. Решить систему линейных уравнений:
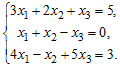
Решение. Способ 1. Метод обратной матрицы.
Введем матрицы: 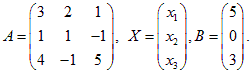
Вычислим определитель матрицы системы
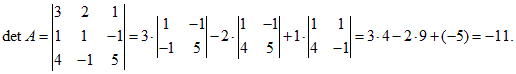
Так как det A ≠ 0, то существует обратная матрица, и решение может быть найдено по формуле X = A–1B.
Найдем алгебраические дополнения элементов матрицы A:
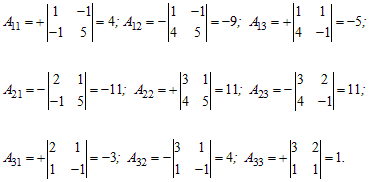
Найдем обратную матрицу по формуле из теоремы 1.1 (главы 1):
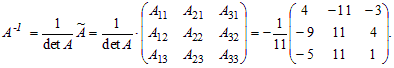
Применяя формулу (4) теоремы 2.1, получим решение системы:
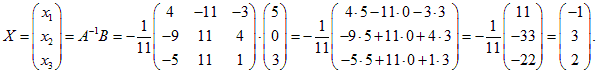
Таким образом, x1 = –1, x2 = 3, x3 = 2.
Способ 2 (по формулам Крамера).
Главный определитель системы уже найден: Δ = det A = –11. Найдем определители Δ1, Δ2, Δ3:
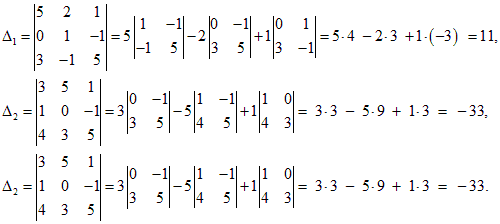
Найдем неизвестные: 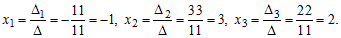
1.2.3. Метод Гаусса решения систем линейных уравнений
Рассмотрим систему m линейных уравнений с n неизвестными:
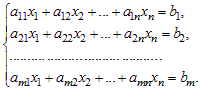
| (1) |
Запишем систему (1) в матричном виде. Для этого введем матрицу A, составленную из коэффициентов системы
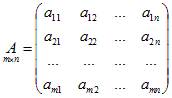 ,
,
матрицу-столбец неизвестных 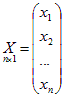
и матрицу-столбец свободных членов 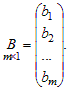
Тогда систему (1) можно заменить одним эквивалентным ей матричным уравнением:
| AX = B | (3) |
Определение. Расширенной матрицей системы (1) называется следующая матрица (A|B) размера m ´ (n + 1):
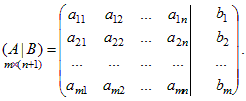
Теорема Кронекера - Капелли
Теорема 2.3. Система (1) совместна тогда и только тогда, когда ранг матрицы A системы равен рангу расширенной матрицы (A|B).
rg A = rg (A|B).
Рассмотрим систему m линейных уравнений с n неизвестными (1). Для ее решения выполним следующие действия.
1) Приведем расширенную матрицу системы (A|B) к ступенчато-му виду посредством элементарных преобразований над строками.
2) Найдем rg A и rg (A|B). Возможны два случая:
● rg A = rg (A|B) Þ система совместна;
● rg A ≠ rg (A|B) Þ система несовместна (не имеет решений).
3) Если система совместна, ищем ее решение следующим образом
С помощью элементарных преобразований над строками расширенной матрицы приведём её к упрощенному виду, когда каждый базисный столбец должен иметь один элемент, равный 1, а остальные нули. Для этого с помощью последней ненулевой строки сделаем нулевыми элементы, стоящие выше единицы в последнем базисном столбце. Затем с помощью предпоследней ненулевой строки сделаем нулевыми элементы, стоящие выше единицы в предпоследнем базисном столбце, и так далее.
Если базисный минор расположен в левом верхнем углу, то матрица (A|B) приводится к следующему упрощенному виду:
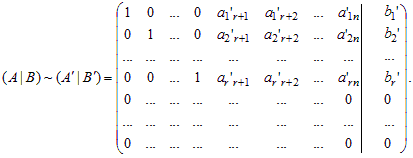
4) Элементарным преобразованиям над строками расширенной матрицы соответствуют преобразования над уравнениями системы. В результате получаем систему, эквивалентную исходной:
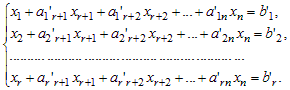
| (5) |
Первые 4 пункта алгоритма составляют прямой ход метода Гаусса. В результате исходная система существенно упрощается.
5) По системе (5) все неизвестные делим на две группы: базисные и свободные. Неизвестные, которым соответствуют столбцы, входящие в базисный минор, называются базисными переменными, остальные неизвестные называются свободными переменными. В системе (5) x1, x2,… xr – базисные переменные, xr+1, x r+2,… xn – свободные переменные. Из системы (5) выражаем базисные переменные через свободные:
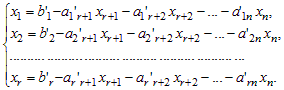
| (6) |
Равенства (6), выражающие базисные переменные через свободные, называются общим решением системы (1). При этом возможны два случая .
● Если rg A = rg (A|B) = n, то система имеет единственное решение (все переменные базисные, свободных переменных нет):
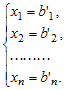
● Если rg A = rg (A|B) = r < n,система имеет бесконечное множество решений, r – базисных переменных и n – r свободных переменных. Множество решений состоит из всех наборов чисел x1, x2,… xn – таких, что свободные переменные xr+1, x r+2,… xn принимают произвольные значения, а базисные переменные x1, x2,… xr находятся по формулам (6).
Определение. Решение системы, полученное из общего решения (6) при конкретных значениях свободных переменных, называется частным решением системы.
Содержание пункта 5 алгоритма составляет обратный ход метода Гаусса.
Пример 1. Решить систему линейных уравнений:
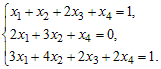
1) Приведем расширенную матрицу системы к ступенчатому виду с помощью элементарных преобразований строк:
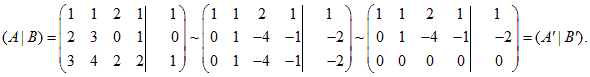
2) Определяем ранги матриц. Матрицы A' и (A'|B') имеют две ненулевых строки, поэтому rg A' = rg (A'|B') = 2. По теореме 1.5 (об инвариантности ранга матрицы) ранги матриц A и (A|B) также равны 2: rg A = rg (A|B) = 2. Следовательно, (по теореме Кронекера-Капелли) система совместна.
3) Приводим матрицу к упрощенному виду. Для этого из первой строки вычитаем вторую:
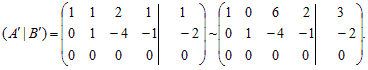
4) Получаем систему уравнений, эквивалентную исходной:
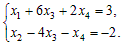
5) Переменные x1, x2 – базисные x3, x4 – свободные. Выразив базисные переменные через свободные, получим общее решение системы:
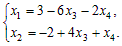
Найдем частное решение. Например, при x3 = 1, x4 = 1 получим x1 = –5, x2 = 3 Следовательно, частное решение имеет вид:
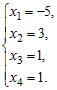
1.2.4. Однородные системы линейных уравнений
Система уравнений называется однородной, если все свободные члены равны нулю:
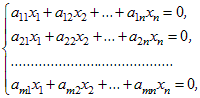
| (7) |
или
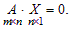
Однородная система всегда совместна, так как имеет тривиальное (нулевое) решение x1 = x2 = ... = xn = 0.
Если ранг матрицы системы равен числу неизвестных (rg A = n), то тривиальное решение единственное. Если ранг матрицы системы меньше числа неизвестных (r = rg A < n), система имеет бесконечно много решений.
Дата: 2018-12-21, просмотров: 349.