Рассмотрим матрицы-строки

A₁ = (a₁₁ a₁₂… a_1n},

A₂ = (a₂₁ a₂₂… a_2n},

………………………

A_k = (a_k1 a_k2… a_kn}

и матрицы-столбцы

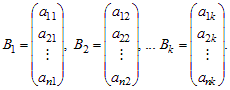
Для краткости матрицы-строки мы будем далее называть просто строками, а матрицы-столбцы просто столбцами.

Определение 1. Линейной комбинацией строк A₁, A₂,… A_k одного размера называется строка c₁A₁ + c₂A₂ +… + c_kA_k , где c₁, c₂,… c_k – произвольные постоянные.

Определение 2. Говорят что строка A линейно выражена через строки A₁, A₂,… A_k, если она представлена в виде их линейной комбинации

A = c₁A₁ + c₂A₂ +… + c_kA_k .

Определение 3. Строки A₁, A₂,… A_k называются линейно зависимыми, если существуют числа c₁, c₂,… c_k, не все равные нулю, такие что линейная комбинация этих строк равна нулевой строке 0:

c₁A₁ + c₂A₂ +… + c_kA_k = 0.

Определение 4. Строки A₁, A₂,… A_k называются линейно независимыми, если их линейная комбинация равна нулевой строке только при c₁ = c₂ = … = c_k = 0:

c₁A₁ + c₂A₂ +… + c_kA_k = 0 Þ c₁ = c₂ = … = c_k = 0.

Все введенные определения аналогично формулируются для столбцов одинакового размера.

Пример 3. Строки A₁ = (1 2 3) и A₂ = (2 4 6) – линейно зависимы, так как A₂ = 2A₁ Þ 2A₁ – A₂ = 0 или 2A₁ + (–1)A₂ = 0. Получили линейную комбинацию с ненулевыми коэффициентами, которая равна нулевой строке.

Пример 4. Строки A₁ = (0 0 0), A₂ = (1 2 3) и A₃ = (3 5 7) – линейно зависимы, так как 1·A₁ + 0·A₂ + 0·A₃ = 0. Получили линейную комбинацию с коэффициентом c₁ = 1 ≠ 0, которая равна нулевой строке.

Пример 5. Рассмотрим строки A₁ = (1 0 0), A₂ = (0 1 0), A₃ = (0 0 1). Докажем, что они линейно независимы. Для этого рассмотрим их линейную комбинацию и приравняем ее к нулевой строке:

c₁A₁ + c₂A₂ + c₃A₃ = (c₁ c₂ c₃) = (0 0 0) = 0.

Равенство возможно только при c₁ = c₂ = c₃ = 0. Значит, строки A₁, A₂ и A₃ линейно независимы.

Теорема 1.4. Система строк A₁, A₂,… A_k линейно зависимая тогда и только тогда, когда одну из строк можно линейно выразить через остальные.

Пример 6. Доказать, что строки A₁ = (1 2 3), A₂ = (2 – 3 4) и A₃ = (3 – 1 7) – линейно зависимы.

Действительно, A₃ = A₁ + A₂. Третья строка линейно выражена через остальные, поэтому система строк линейно зависима.

Свойства линейно зависимых строк.

1) Если система строк содержит нулевую строку, то она линейно зависима.

2) Если система содержит две равные строки, то она линейно зависима.

3) Если система содержит две пропорциональные строки, то она линейно зависима.

4) Если система строк содержит зависимую подсистему строк, то она линейно зависима.

Рассмотрим прямоугольную матрицу размера m ´ n:

.

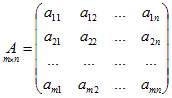Определение 5. Минором k-го порядка матрицы A называется оп-ределитель квадратной матрицы k-го порядка, образованной элементами, стоящими на пересечении любых k строк и любых k столбцов матрицы A.

Пример 7. Найти миноры разных порядков матрицы

.

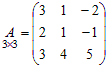Матрица имеет 9 миноров первого порядка, они совпадают с ее элементами: 3, 1, –2, 2, 1, –1, 3, 4, 5.

Девять миноров второго порядка:

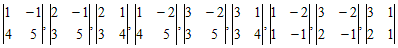
Один минор третьего порядка: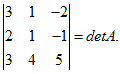

Определение 6. Пусть у матрицы A существует минор k-го порядка, отличный от нуля, а все миноры порядка (k+1) равны нулю, тогда этот минор называется базисным, а строки и столбцы, на пересечении которых он находится, называются базисными строками и базисными столбцами.

Определение7. Рангом матрицы A называется наибольший порядок отличного от нуля минора матрицы, то есть порядок базисного минора. Ранг нулевой матрицы равен нулю по определению. Ранг матрицы A обозначается rg A .

Замечание. Матрица может иметь несколько базисных миноров.

Пример 8. Найти базисный минор, базисные строки, базисные столбцы и ранг матрицы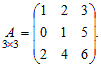

Решение. Минор второго порядка 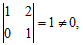минор третьего порядка 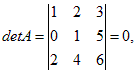так как первая и третья строки пропорциональны. Поэтому 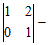базисный минор, первая и вторая строки – базисные; первый и второй столбец – базисные; rg A = 2.