Используя свойства определителя (о перестановке строк или столбцов, о прибавлении ко всем элементам строки или столбца соответствующих элементов параллельного ряда, умноженных на одно и то же число) определитель можно привести к треугольному виду, в котором все элементы, стоящие ниже главной диагонали, равны нулю.

В этом случае определитель равен произведению элементов, стоящих на главной диагонали.

Пример 6. Определитель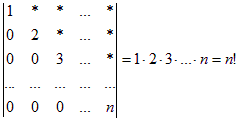

Пример 7. Вычислить определитель 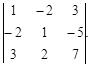, приведя его к треугольному виду.

Решение. Прибавим ко второй строке удвоенную первую:

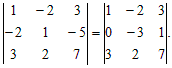
Из третьей строки вычтем утроенную первую:

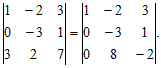
Ко второму столбцу прибавим третий столбец, умноженный на 4:

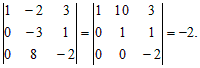
Оглавление

Обратная матрица.

Рассмотрим квадратную матрицу A порядка n:

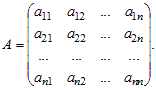
Квадратная матрица называется невырожденной, если её определитель не равен нулю.

Матрица A^–1 называется обратной квадратной матрице A, если

A·A^–1 = A^–1·A = E ..

Рассмотрим матрицу алгебраических дополнений

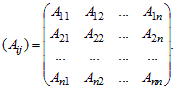
Если транспонировать матрицу алгебраических дополнений, получится новая матрица (A_ij)^T, которая называется присоединенной матрицей матрицы A и обозначается Ã.

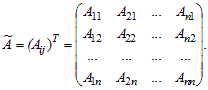
Теорема 1.1. Всякая невырожденная матрица A имеет обратную, которая находится по формуле:

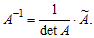
Свойства обратной матрицы

Невырожденные квадратные матрицы одного порядка обладают следующими свойствами.

1) E^–1 = E

2) (A·B)^–1 = B^–1·A^–1

3) (A^T)^–1 = (A^–1)^T

4)

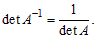
Пример 1. Дана невырожденная квадратная матрица второго порядка 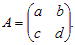Найти обратную матрицу.

Решение. Находим определитель матрицы det A = ad – bc ≠ 0. Вычисляем алгебраические дополнения элементов матрицы: A₁₁ = d; A₁₂ = –c; A₂₁ = –b; A₂₂ = a. Обратную матрицу находим по формуле:

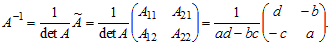
Пример 2. Дана матрица 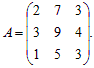Найти обратную.

Решение. Находим определитель матрицы:

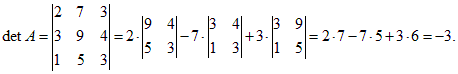
Находим алгебраические дополнения элементов данной матрицы:

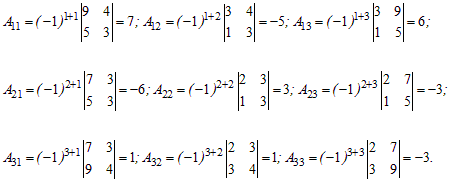
Составим матрицу алгебраических дополнений (A_ij) и, транспонировав ее, найдем присоединенную матрицу Ã:

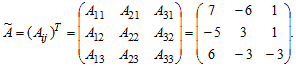
Разделив все элементы присоединенной матрицы Ã на определитель матрицы A, находим обратную матрицу A^–1:

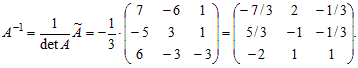
Проверка. Проверим равенство A^–1A = E .

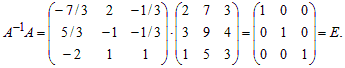
Решение матричных уравнений

Рассмотрим матричное уравнение:

A X = B

где A – квадратная матрица порядка n, B – матрица размера n ´ p.

Теорема 1.2. Если определитель квадратной матрицы A отличен от нуля, то матричное уравнение AX = B имеет единственное решение

X = A^–1B .

Рассмотрим матричное уравнение:

Y A = B

где A – квадратная матрица порядка n, B – матрица размера p ´ n.

Теорема 1.3. Если определитель квадратной матрицы A отличен от нуля, то матричное уравнение YA = B имеет единственное решение

Y = BA^–1.

Пример 3. Даны матрицы 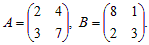Решить уравнения: AX = B и YA = B .

Решение. Найдем обратную матрицу A^–1. Для этого вычислим определитель матрицы det A = 2·7 – 4·3 = 2. Найдем алгебраические дополнения элементов матрицы A:

A₁₁ = 7; A₁₂ = –3; A₂₁ = –4; A₂₂ = 2.

Обратную матрицу находим по формуле:

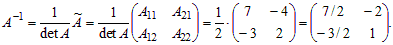
Решение уравнения AX = B находим по формуле из теоремы 1.2:

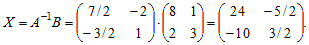
Решение уравнения YA = B находим по формуле из теоремы 1.3:

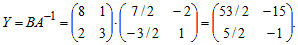
Ранг матрицы.

Элементарные преобразования матриц

Элементарными преобразованиями матриц называются следующие преобразования.

1) Перестановка любых двух строк (столбцов).

2) Умножение всех элементов какой-либо строки (столбца) на одно и то же число, не равное нулю.

3) Прибавление ко всем элементам какой-либо строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число.

Преобразования, обратные к элементарным, также являются элементарными.

Матрица B, полученная из матрицы A с помощью конечного числа элементарных преобразований, называется эквивалентной матрице A. Эквивалентность матриц обозначается так: B ~ A.

Пример 1. Рассмотрим матрицу 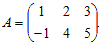Прибавив к пер-вой строке вторую, получим матрицу B, эквивалентную матрице A: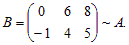

При помощи элементарных преобразований только над строками матрицы, любую матрицу можно привести к следующему виду, называемому ступенчатым:

Высота каждой ступени равна одной строке, первый ненулевой элемент каждой строки равен 1 (каждая ступень начинается с единицы). В начале каждой последующей строки стоит больше нулей, чем в начале предыдущей (за исключением, быть может, нескольких последних нулевых строк).