Пусть λ – любое число, A, B – матрицы, для которых определены операции, записанные в левых частях следующих равенств. Тогда справедливы равенства:

1) (A^T)^T = A

2) (A + B)^T = A^T + B^T

3) (λA)^T = λ(A^T)

4) (AB)^T = B^TA^T

Оглавление

1.1.2. Определители матриц. Определители второго и третьего порядка и их свойства. Миноры и алгебраические дополнения. Вычисление определителей третьего порядка разложением по строке (столбцу). Понятие об определителе n-го порядка. Свойства определителей. Вычисления определителей n-го порядка.

Определители матриц

Рассмотрим квадратную матрицу первого порядка A = (a₁₁).

Определителем матрицы A (или определителем первого порядка) называется число:

det A = |a₁₁| = a₁₁ .

Рассмотрим квадратную матрицу второго порядка

.

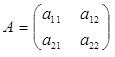Определителем матрицы A (или определителем второго порядка) называется число, равное a₁₁·a₂₂ – a₁₂·a₂₁:

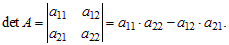
Пример 1. Найти определитель матрицы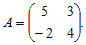

Решение.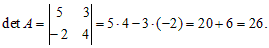

Рассмотрим квадратную матрицу 3-го порядка

.

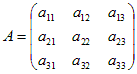Определителем матрицы A (или определителем третьего порядка) называют число, равное

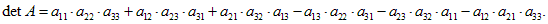
Пример 2. Найти определитель матрицы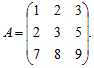

Решение.

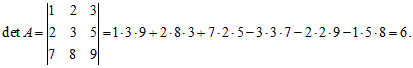
Выражение для определителя 3-го порядка легко запомнить, пользуясь следующим правилом (см. рисунок).

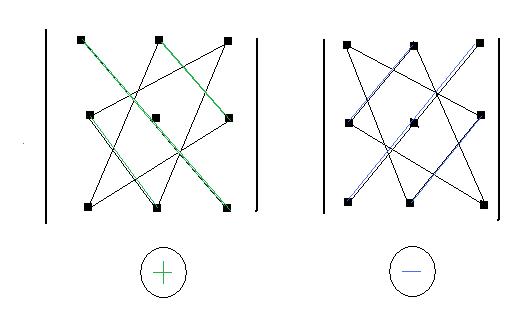
Со знаком « + » берутся произведения элементов, стоящих на главной диагонали и в вершинах двух равнобедренных треугольников с основанием, параллельным главной диагонали. Со знаком « – » берутся произведения элементов, стоящих на побочной диагонали и в вершинах двух равнобедренных треугольников с основанием, параллельным побочной диагонали.

Миноры и алгебраические дополнения

Минором M_ik элемента a_ik определителя называется определитель, получающийся вычеркиванием i-ой строки и k-го столбца.

Алгебраическим дополнением A_ik элемента a_ik называется его минор, взятый со знаком (– 1)^i+k:

A_ik = (– 1)^i+k M_ik.

Пример 3. Найти миноры и алгебраические дополнения элементов a₃₂ и a₁₃ определителя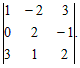

Решение.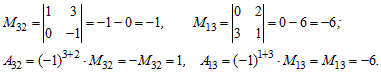

Определитель порядка n и его свойства

Пусть дана квадратная матрица n-го порядка:

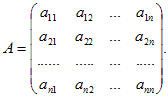
Определителем матрицы A (или определителем порядка n) называется число, равное сумме произведений элементов первой строки на их алгебраические дополнения.

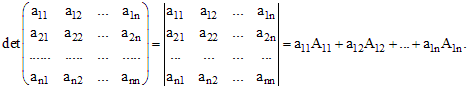
Пример 4.

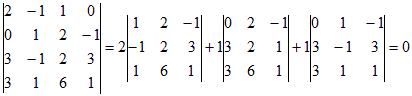
Свойства определителей

Свойство 1. При транспонировании матрицы значение ее определителя не изменится:

det A = det A^T .

Свойство 2. Если поменять местами любые 2 строки (или 2 столбца), то определитель изменит только знак, а по абсолютной величине не изменится.

Следствие. Определитель с двумя одинаковыми строками (столбцами) равен нулю.

Свойство 3. Общий множитель всех элементов строки (или столбца) определителя можно выносить за знак определителя.

Следствие. Определитель с двумя пропорциональными строками (столбцами) равен нулю.

Свойство 4. Если каждый элемент k – го столбца определителя представлен в виде суммы двух слагаемых a_ik = b_ik + c_ik , то данный определитель можно представить в виде суммы двух определителей:

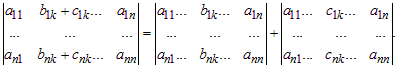
Следствие. Определитель не меняет своего значения, если ко всем элементам какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.

Свойство 5. Определитель произведения двух матриц равен произведению их определителей

det(AB) = detA· detB .

Свойство 6. det(λA) = λⁿdetA .

Свойство 7. Определитель единичной матрицы равен единице:

det E = 1.

Свойство 8. Определитель равен сумме произведений элементов любой его строки (столбца) на их алгебраические дополнения:

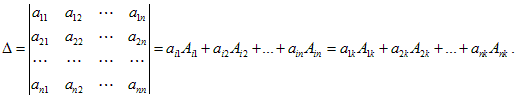
Следствие. Определитель треугольной матрицы равен произведению элементов, стоящих на ее главной диагонали.

Следствие. Определитель диагональной матрицы равен произведению элементов, стоящих на ее главной диагонали.

Пример 5. Вычислить определитель, разложив его по первой строке

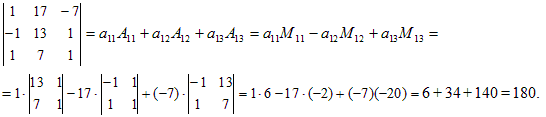
Методы вычисления определителей n-го порядка