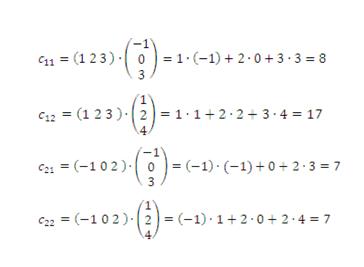Для любых матриц А, В, С, нулевой матрицы О одинакового размера и любых чисел λ и μ справедливы равенства:

1) A + B = B + A;

2) (A + B) + C = A + (B + C);

3) A + O = A;

4) A + (–A) = O;

5) 1·A = A;

6) (λμ)A = λ(μA);

7) (λ + μ)A = λA + μA;

8) λ(A + B) = λA + λB.

Умножение матриц

Произведением матрицы A = (a_ij) размера m ´ n на матрицу B = (b_ij) размера n ´ l называется матрица C = A·B = (c_ij) размера m ´ l, элементы которой c_ij определяются формулой:

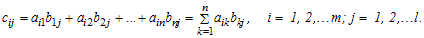
Операция умножения матриц определена только для таких матриц, для которых число столбцов первого сомножителя совпадает с числом строк второго. Заметим, что элемент c_ij, стоящий на пересечении i-й строки и j-го столбца матрицы C, равен сумме попарных произведений соответствующих элементов i-й строки матрицы A и j-го столбца матрицы B:

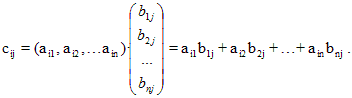
Пример 3. Даны матрицы 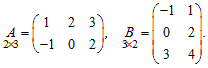Вычислить произведения AB и BA.

Решение. Используя правило умножения, получаем

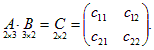
Найдем по определению элементы матрицы C:

В результате получим: .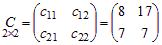

Перемножим матрицы в другом порядке. По правилу умножения

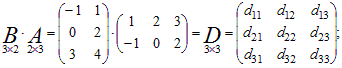
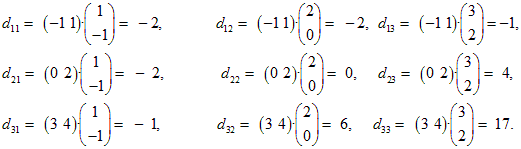
В результате вычислений получим:

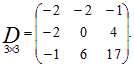
Оба произведения AB и BA определены, но являются матрицами разных размеров, поэтому B ≠ BA.

Свойства операции умножения матриц

Пусть λ – любое число, O – нулевая матрица, А, В, С – произвольные матрицы, для которых определены операции сложения и умножения, записанные в левых частях следующих равенств. Тогда определены операции в правых частях, причем справедливы равенства:

1) (A + B)C = AC + BC;

2) A(B + C) = AB + AC;

3) (AB)C = A(BC);

4) AE = EA = A для любой квадратной матрицы A порядка n и единичной матрицы E того же порядка;

5) AO = OA = O;

6) λ(AB) = (λA)B = A(λB).

Квадратные матрицы A и B одного порядка, для которых AB = BA, называются перестановочными (или коммутирующими).

Пример 4. Рассмотрим квадратные матрицы A и E одного порядка n. По свойству 4 операции умножения они перестановочны. Рассмотрим матрицу λE = diag{λ, λ,… λ}. Тогда по свойствам 6 и 4

A(λE) = λ(AE) = λ(EA) = (λE)A .

Таким образом, матрицы A и λE – перестановочны.

Транспонирование матриц

Если в матрице A заменить строки соответствующими столбцами, то полученная новая матрица A^T называется транспонированной по отношению к матрице A. Пусть

тогда транспонированная матрица имеет вид:

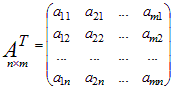
Пример 5. Пусть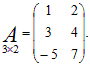

Тогда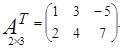

Квадратная матрица порядка n называется симметрической, если

A = A^T

У симметрической матрицы элементы, расположенные симметрично относительно главной диагонали, равны:

a_ij = a_ji при любых i = 1, 2,… n; j = 1, 2,… n.

Пример 6. Матрица 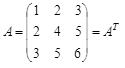– симметрическая.

Квадратная матрица порядка n называется кососимметрической, если A = – A^T

У кососимметрической матрицы элементы, расположенные симметрично относительно главной диагонали, имеют противоположные знаки, а все диагональные элементы равны нулю:

a_ij = – a_ji , a_ii = – a_ii = 0 при любых i = 1, 2,… n; j = 1, 2,… n.

Пример 7. Матрица 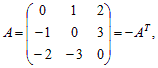поэтому A – кососимметрическая матрица.