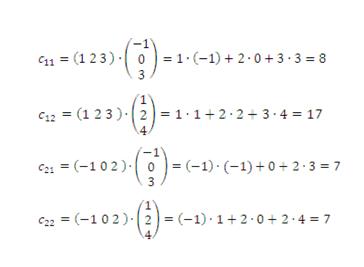Матрицы и действия над ними. Основные операции над матрицами и их свойства
Матрицей размера m ´ n называется прямоугольная таблица чисел, состоящая из m строк и n столбцов:
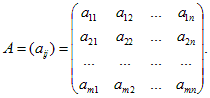
Числа aij называются элементами матрицы, первый индекс i означает номер строки, а второй индекс j – номер столбца, на пересечении которых находится элемент.
Если m = n, матрица называется квадратной, а число m = n – ее порядком.
Рассмотрим квадратную матрицу:

Говорят, что элементы a11, a22,… ann образуют главную диагональ, а элементы an1, an–1, 2,… a1n – побочную диагональ.
Верхней треугольной матрицей называется квадратная матрица, у которой все элементы, стоящие ниже главной диагонали, равны нулю:
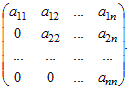
Нижней треугольной матрицей называется квадратная матрица, у которой все элементы, стоящие выше главной диагонали, равны нулю.
Диагональной матрицей называется квадратная матрица, у которой все элементы, не стоящие на главной диагонали, равны нулю:
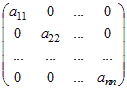
Диагональная матрица обозначается diag{a11, a22,… ann}.
Единичной матрицей называется диагональная матрица, у которой все диагональные элементы равны 1:

Нулевой матрицей называется матрица O, все элементы которой равны нулю.
Матрица, состоящая из одной строки, называется матрицей-строкой:
X = (x1 x2… xn).
Матрица, состоящая из одного столбца, называется матрицей-столбцом:
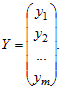
Две матрицы A = (aij) и B = (bij) одинакового размера m ´ n называются равными, если у них равны соответствующие элементы:
aij = bij при любых i = 1, 2,… m; j = 1, 2,… n.
Основные операции над матрицами и их свойства
Сложение матриц
Суммой двух матриц A = (aij) и B = (bij) одинакового размера m ´ n называется матрица C = A + B = (cij) того же размера, элементы которой равны сумме соответствующих элементов матриц A и B:
cij = aij + bij, при любых i = 1, 2,… m; j = 1, 2,… n.
Пример 1. Найти сумму двух матриц
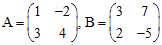
Решение. Складывая соответствующие элементы матриц, получаем:
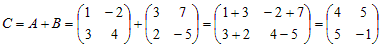
Умножение матрицы на число
Произведением матрицы A = (aij) размера m ´ n на число λ называется матрица С = λ·A = A·λ = (cij) того же размера, элементы которой равны соответствующим элементам матрицыA, умноженным на число λ:
cij = λ aij при любых i = 1, 2,… m; j = 1, 2,… n.
Пример 2. Найти произведение матрицы 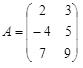 на число λ.
на число λ.
Решение. Умножив на λ каждый элемент матрицы A, получим
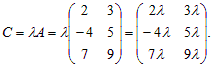
Вычитание матриц
Разностью двух матриц A и В одинакового размера m ´ n называется матрица
A–В=A+ (–1) В.
Матрица (–A) = (–1)A называется противоположной матрице A.
Свойства операций сложения и умножения на число
Для любых матриц А, В, С, нулевой матрицы О одинакового размера и любых чисел λ и μ справедливы равенства:
1) A + B = B + A;
2) (A + B) + C = A + (B + C);
3) A + O = A;
4) A + (–A) = O;
5) 1·A = A;
6) (λμ)A = λ(μA);
7) (λ + μ)A = λA + μA;
8) λ(A + B) = λA + λB.
Умножение матриц
Произведением матрицы A = (aij) размера m ´ n на матрицу B = (bij) размера n ´ l называется матрица C = A·B = (cij) размера m ´ l, элементы которой cij определяются формулой:
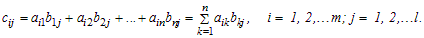
Операция умножения матриц определена только для таких матриц, для которых число столбцов первого сомножителя совпадает с числом строк второго. Заметим, что элемент cij, стоящий на пересечении i-й строки и j-го столбца матрицы C, равен сумме попарных произведений соответствующих элементов i-й строки матрицы A и j-го столбца матрицы B:
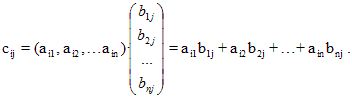
Пример 3. Даны матрицы 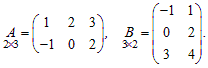 Вычислить произведения AB и BA.
Вычислить произведения AB и BA.
Решение. Используя правило умножения, получаем
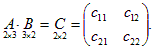
Найдем по определению элементы матрицы C:
|
В результате получим: 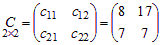 .
.
Перемножим матрицы в другом порядке. По правилу умножения
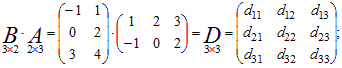
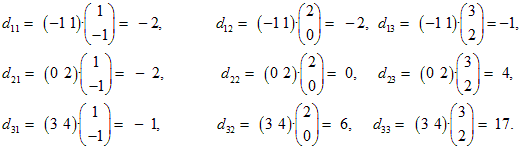
В результате вычислений получим:


Оба произведения AB и BA определены, но являются матрицами разных размеров, поэтому B ≠ BA.
Транспонирование матриц
Если в матрице A заменить строки соответствующими столбцами, то полученная новая матрица AT называется транспонированной по отношению к матрице A. Пусть

тогда транспонированная матрица имеет вид:

Пример 5. Пусть 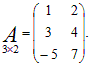
Тогда 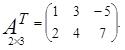
Квадратная матрица порядка n называется симметрической, если
A = AT
У симметрической матрицы элементы, расположенные симметрично относительно главной диагонали, равны:
aij = aji при любых i = 1, 2,… n; j = 1, 2,… n.
Пример 6. Матрица 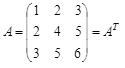 – симметрическая.
– симметрическая.
Квадратная матрица порядка n называется кососимметрической, если A = – AT
У кососимметрической матрицы элементы, расположенные симметрично относительно главной диагонали, имеют противоположные знаки, а все диагональные элементы равны нулю:
aij = – aji , aii = – aii = 0 при любых i = 1, 2,… n; j = 1, 2,… n.
Пример 7. Матрица 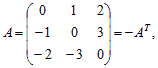 поэтому A – кососимметрическая матрица.
поэтому A – кососимметрическая матрица.
Свойства определителей
Свойство 1. При транспонировании матрицы значение ее определителя не изменится:
det A = det AT .
Свойство 2. Если поменять местами любые 2 строки (или 2 столбца), то определитель изменит только знак, а по абсолютной величине не изменится.
Следствие. Определитель с двумя одинаковыми строками (столбцами) равен нулю.
Свойство 3. Общий множитель всех элементов строки (или столбца) определителя можно выносить за знак определителя.
Следствие. Определитель с двумя пропорциональными строками (столбцами) равен нулю.
Свойство 4. Если каждый элемент k – го столбца определителя представлен в виде суммы двух слагаемых aik = bik + cik , то данный определитель можно представить в виде суммы двух определителей:

Следствие. Определитель не меняет своего значения, если ко всем элементам какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.
Свойство 5. Определитель произведения двух матриц равен произведению их определителей
det(AB) = detA· detB .
Свойство 6. det(λA) = λndetA .
Свойство 7. Определитель единичной матрицы равен единице:
det E = 1.
Свойство 8. Определитель равен сумме произведений элементов любой его строки (столбца) на их алгебраические дополнения:
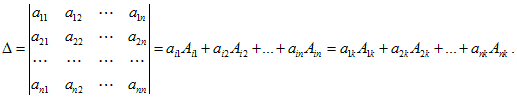
Следствие. Определитель треугольной матрицы равен произведению элементов, стоящих на ее главной диагонали.
Следствие. Определитель диагональной матрицы равен произведению элементов, стоящих на ее главной диагонали.
Пример 5. Вычислить определитель, разложив его по первой строке
Методы вычисления определителей n-го порядка
Обратная матрица.
Рассмотрим квадратную матрицу A порядка n:
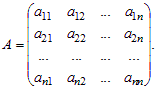
Квадратная матрица называется невырожденной, если её определитель не равен нулю.
Матрица A–1 называется обратной квадратной матрице A, если
A·A–1 = A–1·A = E ..
Рассмотрим матрицу алгебраических дополнений
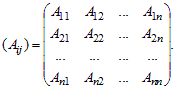
Если транспонировать матрицу алгебраических дополнений, получится новая матрица (Aij)T, которая называется присоединенной матрицей матрицы A и обозначается Ã.
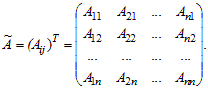
Теорема 1.1. Всякая невырожденная матрица A имеет обратную, которая находится по формуле:
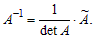
Свойства обратной матрицы
Невырожденные квадратные матрицы одного порядка обладают следующими свойствами.
1) E–1 = E
2) (A·B)–1 = B–1·A–1
3) (AT)–1 = (A–1)T
4) 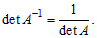
Пример 1. Дана невырожденная квадратная матрица второго порядка 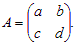 Найти обратную матрицу.
Найти обратную матрицу.
Решение. Находим определитель матрицы det A = ad – bc ≠ 0. Вычисляем алгебраические дополнения элементов матрицы: A11 = d; A12 = –c; A21 = –b; A22 = a. Обратную матрицу находим по формуле:
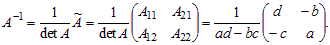
Пример 2. Дана матрица  Найти обратную.
Найти обратную.
Решение. Находим определитель матрицы:
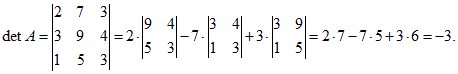
Находим алгебраические дополнения элементов данной матрицы:
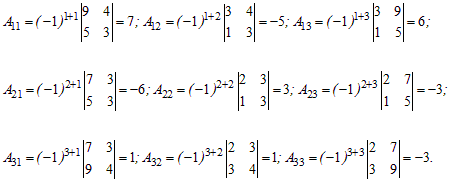
Составим матрицу алгебраических дополнений (Aij) и, транспонировав ее, найдем присоединенную матрицу Ã:
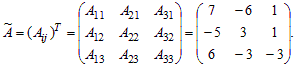
Разделив все элементы присоединенной матрицы Ã на определитель матрицы A, находим обратную матрицу A–1:

Проверка. Проверим равенство A–1A = E .
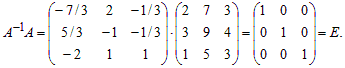
Решение матричных уравнений
Рассмотрим матричное уравнение:
A X = B
где A – квадратная матрица порядка n, B – матрица размера n ´ p.
Теорема 1.2. Если определитель квадратной матрицы A отличен от нуля, то матричное уравнение AX = B имеет единственное решение
X = A–1B .
Рассмотрим матричное уравнение:
Y A = B
где A – квадратная матрица порядка n, B – матрица размера p ´ n.
Теорема 1.3. Если определитель квадратной матрицы A отличен от нуля, то матричное уравнение YA = B имеет единственное решение
Y = BA–1.
Пример 3. Даны матрицы 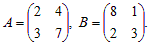 Решить уравнения: AX = B и YA = B .
Решить уравнения: AX = B и YA = B .
Решение. Найдем обратную матрицу A–1. Для этого вычислим определитель матрицы det A = 2·7 – 4·3 = 2. Найдем алгебраические дополнения элементов матрицы A:
A11 = 7; A12 = –3; A21 = –4; A22 = 2.
Обратную матрицу находим по формуле:
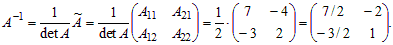
Решение уравнения AX = B находим по формуле из теоремы 1.2:
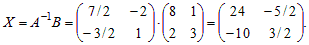
Решение уравнения YA = B находим по формуле из теоремы 1.3:
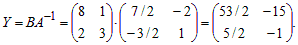
Ранг матрицы.
Элементарные преобразования матриц
Элементарными преобразованиями матриц называются следующие преобразования.
1) Перестановка любых двух строк (столбцов).
2) Умножение всех элементов какой-либо строки (столбца) на одно и то же число, не равное нулю.
3) Прибавление ко всем элементам какой-либо строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число.
Преобразования, обратные к элементарным, также являются элементарными.
Матрица B, полученная из матрицы A с помощью конечного числа элементарных преобразований, называется эквивалентной матрице A. Эквивалентность матриц обозначается так: B ~ A.
Пример 1. Рассмотрим матрицу 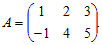 Прибавив к пер-вой строке вторую, получим матрицу B, эквивалентную матрице A:
Прибавив к пер-вой строке вторую, получим матрицу B, эквивалентную матрице A: 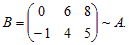
При помощи элементарных преобразований только над строками матрицы, любую матрицу можно привести к следующему виду, называемому ступенчатым:

Высота каждой ступени равна одной строке, первый ненулевой элемент каждой строки равен 1 (каждая ступень начинается с единицы). В начале каждой последующей строки стоит больше нулей, чем в начале предыдущей (за исключением, быть может, нескольких последних нулевых строк).
Тема 1.2. Линейная алгебра.
Теорема Кронекера - Капелли
Теорема 2.3. Система (1) совместна тогда и только тогда, когда ранг матрицы A системы равен рангу расширенной матрицы (A|B).
rg A = rg (A|B).
Рассмотрим систему m линейных уравнений с n неизвестными (1). Для ее решения выполним следующие действия.
1) Приведем расширенную матрицу системы (A|B) к ступенчато-му виду посредством элементарных преобразований над строками.
2) Найдем rg A и rg (A|B). Возможны два случая:
● rg A = rg (A|B) Þ система совместна;
● rg A ≠ rg (A|B) Þ система несовместна (не имеет решений).
3) Если система совместна, ищем ее решение следующим образом
С помощью элементарных преобразований над строками расширенной матрицы приведём её к упрощенному виду, когда каждый базисный столбец должен иметь один элемент, равный 1, а остальные нули. Для этого с помощью последней ненулевой строки сделаем нулевыми элементы, стоящие выше единицы в последнем базисном столбце. Затем с помощью предпоследней ненулевой строки сделаем нулевыми элементы, стоящие выше единицы в предпоследнем базисном столбце, и так далее.
Если базисный минор расположен в левом верхнем углу, то матрица (A|B) приводится к следующему упрощенному виду:
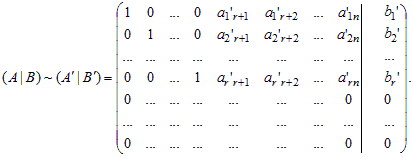
4) Элементарным преобразованиям над строками расширенной матрицы соответствуют преобразования над уравнениями системы. В результате получаем систему, эквивалентную исходной:
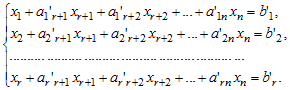
| (5) |
Первые 4 пункта алгоритма составляют прямой ход метода Гаусса. В результате исходная система существенно упрощается.
5) По системе (5) все неизвестные делим на две группы: базисные и свободные. Неизвестные, которым соответствуют столбцы, входящие в базисный минор, называются базисными переменными, остальные неизвестные называются свободными переменными. В системе (5) x1, x2,… xr – базисные переменные, xr+1, x r+2,… xn – свободные переменные. Из системы (5) выражаем базисные переменные через свободные:
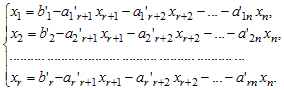
| (6) |
Равенства (6), выражающие базисные переменные через свободные, называются общим решением системы (1). При этом возможны два случая .
● Если rg A = rg (A|B) = n, то система имеет единственное решение (все переменные базисные, свободных переменных нет):

● Если rg A = rg (A|B) = r < n,система имеет бесконечное множество решений, r – базисных переменных и n – r свободных переменных. Множество решений состоит из всех наборов чисел x1, x2,… xn – таких, что свободные переменные xr+1, x r+2,… xn принимают произвольные значения, а базисные переменные x1, x2,… xr находятся по формулам (6).
Определение. Решение системы, полученное из общего решения (6) при конкретных значениях свободных переменных, называется частным решением системы.
Содержание пункта 5 алгоритма составляет обратный ход метода Гаусса.
Пример 1. Решить систему линейных уравнений:
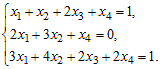
1) Приведем расширенную матрицу системы к ступенчатому виду с помощью элементарных преобразований строк:
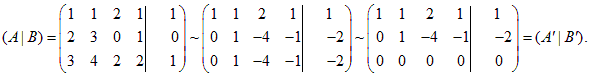
2) Определяем ранги матриц. Матрицы A' и (A'|B') имеют две ненулевых строки, поэтому rg A' = rg (A'|B') = 2. По теореме 1.5 (об инвариантности ранга матрицы) ранги матриц A и (A|B) также равны 2: rg A = rg (A|B) = 2. Следовательно, (по теореме Кронекера-Капелли) система совместна.
3) Приводим матрицу к упрощенному виду. Для этого из первой строки вычитаем вторую:

4) Получаем систему уравнений, эквивалентную исходной:
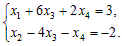
5) Переменные x1, x2 – базисные x3, x4 – свободные. Выразив базисные переменные через свободные, получим общее решение системы:
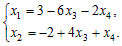
Найдем частное решение. Например, при x3 = 1, x4 = 1 получим x1 = –5, x2 = 3 Следовательно, частное решение имеет вид:
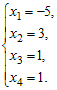
1.2.4. Однородные системы линейных уравнений
Система уравнений называется однородной, если все свободные члены равны нулю:
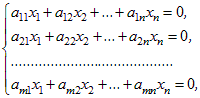
| (7) |
или

Однородная система всегда совместна, так как имеет тривиальное (нулевое) решение x1 = x2 = ... = xn = 0.
Если ранг матрицы системы равен числу неизвестных (rg A = n), то тривиальное решение единственное. Если ранг матрицы системы меньше числа неизвестных (r = rg A < n), система имеет бесконечно много решений.
Сложение векторов
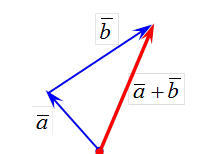
|
| Рис.6 |
Определение. Суммой двух векторов ā и  называется вектор ā +`b, идущий из начала вектора ā в конец вектора `b при условии, что вектор`b приложен к концу
называется вектор ā +`b, идущий из начала вектора ā в конец вектора `b при условии, что вектор`b приложен к концу
вектора ā (рис.7).
Это правило сложения векторов называют правилом треугольника.
Умножение вектора на число
Пусть дан вектор ā и действительное число l, |ā| – длина вектора ā, |l| – абсолютная величина (модуль) числа l (лямбда).
Определение. Произведением вектора ā на число l называется вектор lā (или āl), обладающий следующими свойствами:
1) длина вектора lā равна произведению длины вектора ā на абсолютную величину числа l, т. е. |lā| = |l||ā|;
2) вектор lā коллинеарен вектору ā (lā || ā), причем,
если l > 0, то lā ↑↑ ā;
если l < 0, то lā ↑↓ ā;
если l = 0, то lā = 0.
Замечание. При умножении вектора на l = –1 его длина не изменяется, а направление меняется на противоположное, поэтому вектор –ā называется противоположным вектору ā.
Разность двух векторов.
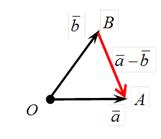
|
| Рис.10 |
Определение. Разностью двух векторов ā и`b называется вектор ā –`b, который в сумме с вектором`b дает вектор ā (рис.10).
Рассмотрим векторы ā и`b. Приведем их к общему началу O. Обозначим: 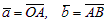 . Тогда, согласно данному определению:
. Тогда, согласно данному определению:  .
.
Разность векторов ā и`b можно рассматривать как сумму вектора ā и вектора (–`b), противоположного`  , т.е. как ā +( –`b).
, т.е. как ā +( –`b).
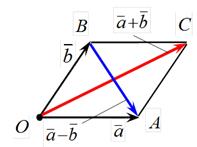
|
Рис.11 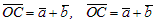 , ,
|
Замечание. Если векторы ā и  приведены к общему началу и на них, как на сторонах, построен параллелограмм (рис. 11), то та из диагоналей этого параллелограмма, которая
приведены к общему началу и на них, как на сторонах, построен параллелограмм (рис. 11), то та из диагоналей этого параллелограмма, которая
выходит из их общего начала, является суммой векторов: 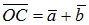 , а вторая диагональ
, а вторая диагональ 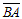 является разностью векторов:
является разностью векторов: 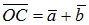 .
.
Определение. Единичным вектором называется вектор, длина которого равна единице, т.е. |ā| = 1.
Определение. Орт вектора ā – это единичный вектор, сонаправленный с вектором ā.
Орт вектора ā обозначается ā0 (ā0 ↑↑ ā, |ā0| = 1).
Согласно этому определению: ā = |ā| ā0 или 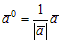 .
.
1.3.3. Необходимое и достаточное условие коллинеарности двух векторов.
Теорема. Для того, чтобы два вектора ā и`b были коллинеарны, необходимо и достаточно, чтобы один из них мог быть представлен в виде произведения некоторого числа на другой вектор, т. е. 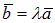 (или
(или 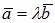 ).
).
В этой теореме мы должны доказать два признака; один из них является необходимым для данного утверждения, а другой достаточным.
Такая формулировка теоремы встречается нам впервые. Уточним, в каком случае признак называется необходимым для данного утверждения, а в каком - достаточным.
Пусть имеется некоторое утверждение и какой-либо признак для проверки справедливости этого утверждения.
Если из справедливости данного утверждения следует выполнение признака, то такой признак называется необходимым для данного утверждения.
Если же наоборот – из выполнения признака следует справедливость данного утверждения, то такой признак называется достаточным для данного утверждения.
Признак может быть только необходимым, или только достаточным, или одновременно и достаточным, и необходимым.
Доказательство теоремы разобьем на две части.
i) Докажем необходимость. Если один из векторов, например, `b =`0, то `b = 0·ā = lā (при l = 0) и теорема доказана).
Пусть векторы ā и `b коллинеарны, ā ¹ 0 и`b ¹ 0. Докажем, что существует действительное число l такое, что `b = lā.
Рассмотрим орты векторов ā и `b:  .
.
а) Если векторы ā и`b сонаправлены, то ā0 =`b 0, т. е. 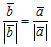 или
или 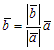 . Обозначив
. Обозначив 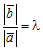 , получим `b = lā. Заметим, что в этом случае l > 0.
, получим `b = lā. Заметим, что в этом случае l > 0.
б) Если векторы ā и`b направлены противоположно, то ā0 = –`b 0, т. е. 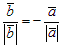 или
или 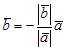 . Обозначив
. Обозначив  , получим `b = lā.
, получим `b = lā.
Заметим, что в этом случае l < 0. Таким образом, если векторы ā и`b коллинеарны, то`b = lā.
ii) Докажем достаточность. Пусть даны два вектора ā и`b, и известно, что существует число l такое, что`b = lā. Надо доказать, что ā ||`b.
Доказательство этого утверждения немедленно следует из определения умножения вектора на число.
Свойства проекций

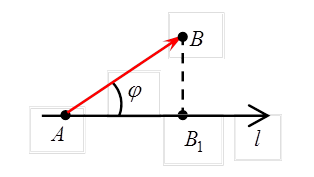
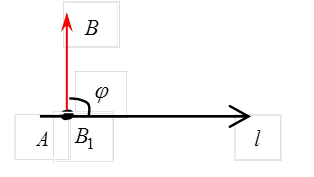
Доказательство. Рассмотрим отдельно случаи: а) угол наклона вектора к оси острый, б) угол наклона вектора к оси тупой, в) вектор перпендикулярен к оси.
|
| Рис.4 |
а) Пусть 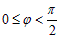 (рис.4), тогда из DABB1:
(рис.4), тогда из DABB1: 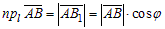 .
.
|
| Рис.5 |
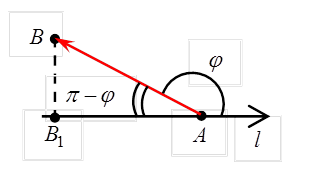
б) Пусть 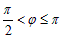 (рис 5), тогда из DABB1:
(рис 5), тогда из DABB1:
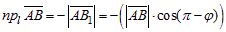 , т.е.
, т.е. 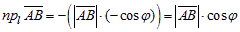
|
| Рис.6 |
в) Пусть  (рис.6), тогда
(рис.6), тогда  .
.
Окончательно для любого случая
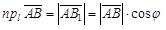


Замечание. Это свойство с помощью обычной индукции легко распространить на сумму любого конечного числа векторов.

Скалярное произведение двух векторов, определение, свойства, физический смысл скалярного произведения. Вычисление скалярного произведения в прямоугольной системе координат. Направляющие косинусы вектора.
Уравнение прямой в отрезках
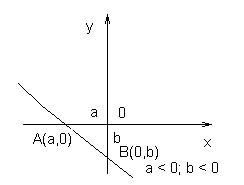
Если прямая отсекает на осях отрезки а и b, не равные нулю, то ее уравнение имеет вид:
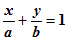
| (1.5.8) |
Такое уравнение называется уравнением прямой в отрезках. Рассмотрим это уравнение. Пусть x = 0, тогда 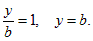 Пусть y = 0, тогда
Пусть y = 0, тогда 
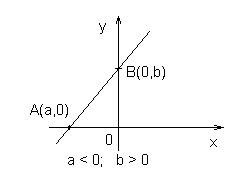
Прямая проходит через точки А(а, 0) и B(0, b) (рис. 1.5.19 – рис.1.5.21).

| 
| 
|
| Рис. 1.5.19 | Рис. 1.5.20 | Рис. 1.5.21 |
Пример. Записать уравнение прямой 3x – 2y + 12 = 0 в отрезках и построить эту прямую.
Решение: 3x – 2y = –12. Разделим обе части этого уравнения на –12. Получим:
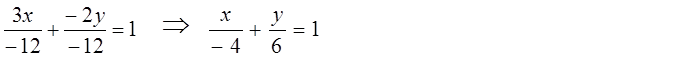
Следовательно, a = –4, b = 6.
Построим эту прямую. Для этого отложим на оси Ox a = –4, на оси Oy b = 6 и соединим полученные точки.
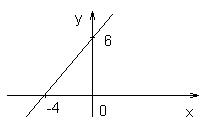
Рис. 1.5.22
Общее уравнение плоскости
Уравнение
| Ax + By + Cz + D = 0 | (1.6.2) |
называется общим уравнением плоскости, здесь ` N = (A; B; C) – нормальный вектор.
Рассмотрим частные случаи этого уравнения.
1) Пусть D = 0. Уравнение имеет вид: Ax + By + Cz = 0.
Такая плоскость проходит через начало координат.
Ее нормальный вектор 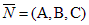 .
.
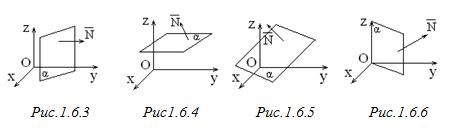
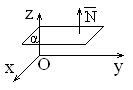
2) С = 0: Ax + By + D = 0 Нормальный вектор этой плоскости 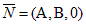 перпендикулярен оси Oz Þ плоскость параллельна оси Oz (рис.1.6.3)
перпендикулярен оси Oz Þ плоскость параллельна оси Oz (рис.1.6.3)
3) B = 0: Ax + Cz + D = 0 Þ` 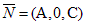 ^ Oy,
^ Oy,
плоскость параллельна оси Oy (рис. 1.6.4)
4) A = 0: By + Cz + D = 0 Þ` N = (0; B; C) ^ Ox, плоскость параллельна оси Ox (рис. 5)
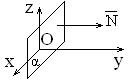
5) C = D = 0: Ax + By = 0 Þ` 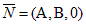 ^ Oz, плоскость проходит через ось Oz (рис. 1.6.6)
^ Oz, плоскость проходит через ось Oz (рис. 1.6.6)
| 
| 
|
| Рис.1.6.7 | Рис.1.6.8 | Рис.1.6.9 |
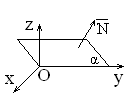
6) B = D = 0: Ax + Cz = 0 Þ` N = (A; 0; C) ^ Oy, плоскость проходит через ось Oy (рис. 1.6.7)
7) A = D = 0: By + Cz = 0 Þ` N = (0; B; C) ^ Ox, плоскость проходит через ось Ox (рис. 1.6.8)
8) A = B = 0: Cz + D = 0 Þ` N = (0; 0; C) || Oz, плоскость параллельна плоскости Oxy (рис. 1.6.9)

|
|
| Рис.1.6.10 | Рис.1.6.11 |
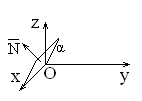
9) B = C = 0: Ax + D = 0 Þ` N = (A; 0; 0) || Ox, плоскость параллельна плоскости Oyz (рис. 1.6.10)
10) A = C = 0: By + D = 0 Þ` N = (0; B; 0) || Oy, плоскость параллельна плоскости Oxz (рис. 1.6.11)
Пример. Составить уравнение плоскости, проходящей через
точку M0(1; 2; –1) перпендикулярно вектору` N = (2; –1; 3). Найти точки пересечения этой плоскости с осями координат.
Решение. По формуле (1.6.1) имеем
2(x – 1) –1·(y – 2) + 3(z + 1) =0, 2x – y + 3z + 3 = 0.
Для того, чтобы найти пересечение этой плоскости с осью Ox, подставим в полученное уравнение y = 0, z = 0. Получим 2x + 3 = 0; x = –1,5.
Точка пересечения искомой плоскости с осью Ox имеет координаты:
M1(–1,5; 0; 0). Найдем пересечение плоскости с осью Oy. Для этого возьмем x = 0, z = 0. Имеем – y + 3 = 0 Þ y = 3. Итак, M2(0; 3; 0).
Для нахождения точки пересечения с осью Oz возьмем x = 0, y = 0. Тогда 3z + 3 = 0 Þ z = – 1. Итак, M3(0; 0; –1).
Ответ: 2x – y + 3z + 3 = 0, M1(–1,5; 0; 0), M2(0; 3; 0), M3(0; 0; –1).
Пример. Исследовать плоскости, заданные уравнениями:
a) 3x – y + 2z = 0, б) 2x + z – 1 = 0, в) –y + 5 = 0, г) x = 0.
Решение. а) Данная плоскость проходит через начало координат (D = 0) и имеет нормальный вектор` N = (3; –1; 2).
б) В уравнении 2x + z – 1 = 0 коэффициент B = 0. Следовательно,
N = (2; 0; 1). Плоскость параллельна оси Oy.
в) В уравнении –y + 5 = 0 коэффициенты A = 0, C = 0. Значит,` N = (0; –1; 0). Плоскость параллельна плоскости Oxy.
г) Уравнение x = 0 задает плоскость Oyz, так как при B = 0, C = 0 плоскость параллельна плоскости Oyz, а из условия D = 0 следует, что плоскость проходит через начало координат.
Пример. Составить уравнение плоскости, проходящей через точку A(2; 3; 1) и перпендикулярной вектору 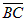 , где B(1; 0; –1), C(–2; 2; 0).
, где B(1; 0; –1), C(–2; 2; 0).
Решение. Найдем вектор 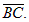
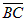 = (–2 – 1; 2 – 0; 0 –(–1)) = (–3; 2; 1).
= (–2 – 1; 2 – 0; 0 –(–1)) = (–3; 2; 1).
Вектор 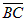 является нормальным вектором искомой плоскости, проходящей через точку A(2; 3; 1) По формуле (2.2.1) имеем:
является нормальным вектором искомой плоскости, проходящей через точку A(2; 3; 1) По формуле (2.2.1) имеем:
–3(x – 2) + 2(y – 3) + 1·(z – 1) = 0; –3x + 2y + z + 6 – 6 – 1 = 0;
–3x + 2y + z – 1 = 0; 3x – 2y – z + 1 = 0.
Ответ: 3x – 2y – z + 1 = 0.
Окружность
Под окружностью понимают геометрическое место точек, равноудаленных от некоторой фиксированной точки, называемой центром окружности.
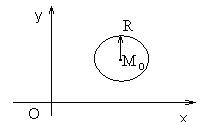
Рис. 1.7.1.
Пусть дана точка M0(x0, y0) и некоторое число R (R ≥ 0).
Уравнение окружности радиуса R с центром в точке M0 имеет вид:
| (x – x0)2 + (y – y0)2 = R2 | (1.7.1.) |
Если центр окружности M0 находится в точке О(0,0), то уравнение (1.7.1) будет иметь вид:
| x 2 + y2 = R2 | (1.7.2) |
Пример. Установить вид кривых второго порядка, заданных уравнениями:
a) x2 + y2 + 6x – 4y – 3 = 0
б) x2 + y2 + 4x – 2y + 5 = 0
в) x2 + y2 + – 2x + 4y + 7 = 0
Решение:
а) Перепишем данное уравнение, выделяя полный квадрат:
x2 + 2·3x + 9 – 9 + y2 – 2·2y + 4 – 4 – 3 = 0
(x + 3)2 + (y – 2)2 = 16
Данное уравнение определяет окружность радиуса 4 с центром
в точке M0(–3, 2).
б) Преобразуем данное уравнение, также выделяя полный квадрат
x2 + 2·2x + 4 – 4 + y2 – 2·y + 1 – 1 + 5 = 0
(x + 2)2 + (y – 1)2 = 0.
Полученное равенство возможно лишь при x = –2, y = 1. Данное уравнение определяет только одну точку M(–2, 1).
в) Преобразуем данное уравнение аналогично:
x2 –2x + 1 – 1 + y2 + 2·y + 4 – 4 + 7 = 0
(x – 1)2 + (y + 2)2 = –2.
Это уравнение не имеет решения. Следовательно, не существует точек, удовлетворяющих данному уравнению.
Эллипс
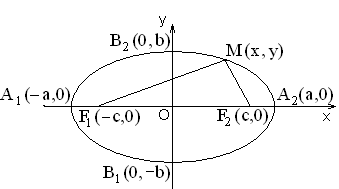
Рис.1.7.2.
Эллипсом называется геометрическое место точек плоскости, сумма расстояний от которых до двух данных точек, называемых фокусами, есть величина постоянная.
Обозначим фокусы F1 и F2 расстояние между ними |F1F2| = 2c. Пусть |MF1| + |MF2| = 2a. С помощью алгебраических преобразований можно получить уравнение эллипса:
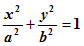
| (1.7.3) |
,где b2 = a2 – c2 > 0, так как a > c. (см. рис.1.7.1.).
Уравнение (1.7.3) называется каноническим уравнением эллипса. Точка О(0,0) является центром эллипса. Величины a и b (где а > 0 и b > 0) называются полуосями эллипса (отрезки 2аи 2b являются, соответственно, осями эллипса). Центр эллипса может находиться в произвольной точке M0(x0, y0). Уравнение эллипса с центром в точке M0(x0, y0) и осями, параллельными координатным осям, имеет вид:
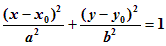
| (1.7.4) |
Пример. Показать, что уравнение 4x2 + 9y2 – 16x – 18y – 11 = 0 определяет эллипс. Сделать чертеж.
Решение: Преобразуем данное уравнение, выделяя полный квадрат: 4x2 + 9y2 – 16x – 18y – 11 = 0 Þ
4(x2 – 2·2x + 4 – 4) + 9(y2 – 2y + 1 – 1) – 11 = 0 Þ
4((x – 2)2·– 4) + 9((y – 1)2 – 1) – 11 = 0 Þ 4((x – 2)2·+9(y – 1)2 = 36.
Разделим обе части полученного уравнения на 36:

Получили уравнение эллипса вида (1.7.4) с центром в точке M0(2,1) и полуосями а = 3, b = 2.
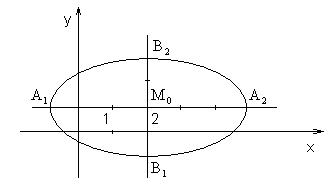
Рис.1.7.3
Для построения эллипса отметим в плоскости Oxy точку M0(2, 1) и проведем через эту точку прямые, параллельные осям Ox и Oy. Отметим на горизонтальной прямой точки A1 и A2отстоящие от M0 на 3 единицы; на вертикальной прямой – точки B1 и B2 отстоящие от M0 на 2 единицы. Точки A1, B2, A2, B1 соединим плавной линией. Эллипс построен.
| |
Полярные координаты
Полярная система координат на плоскости (рис.1.7.10) определяется заданием некоторой точки О, луча ОР, исходящего из этой точки, и единицы масштаба. Точка О называетсяполюсом, а луч ОР – полярной осью.
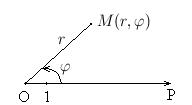
Рис.1.7.10
Пусть M – произвольная точка плоскости. Обозначим через r расстояние от точки M до полюса, через j – угол, отсчитываемый от полярной оси против часовой стрелки до направленияОМ. Эти числа называются полярными координатами точки М, причем величина r называется полярным радиусом, а j – полярным углом точки М. По определению величина r = |OM|. Задание пары чисел (r, j) однозначно определяет точку М на плоскости.
Если ограничить изменение угла j пределами 0 ≤ j ≤ 2p, то верно и обратное каждой точке плоскости однозначно соответствует пара чисел (r, j). Исключение составляет только полюсО, для которого r = 0, а угол j не определен.
Если выбрать декартову систему координат так, чтобы ее начало совпадало с полюсом полярной системы, а ось Ox шла по полярной оси ОР, то декартовы координаты (x, y) произвольной точки М и ее полярные координаты (r, j) будут связаны следующими соотношениями:
| x = rcos j , y = rsin j | (1.7.1) |
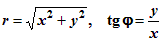
| (1.7.2) |
Из этих формул следует, что
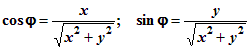
| (1.7.3) |
Замечание: Формула tg j = y/x определяет два угла j и j + p (в пределах от 0 до 2p).
Формулы (1.7.3) уточняют, какой из этих углов следует выбрать. Из формулы  вытекает, что надо брать тот угол j, для которого cos j имеет тот же знак, что и x.
вытекает, что надо брать тот угол j, для которого cos j имеет тот же знак, что и x.
Пример. Построить точки, заданные своими полярными координатами:
A(3; p/2), B(2; 5p/4), C(1; –p/4), D(2; 0).
Решение: Для построения точек A, B и С из полюса О проведем лучи под углом j1 = p/2, j2 = 5p/4, j3 = –p/4 и на них отложим отрезки длины 3, 2, 1, соответственно (рис.1.7.11).

Рис.1.7.11
Точку D откладываем на полярной оси на расстоянии 2 от полюса.
Пример. Построить линию, заданную в полярной системе координат уравнением r = 2cos j .
Решение: Построим эту линию по точкам, придавая углу j определенные значения и получая значения r из уравнения r = 2cos j.
Если j = 0 Þ r = 2cos0 = 2.
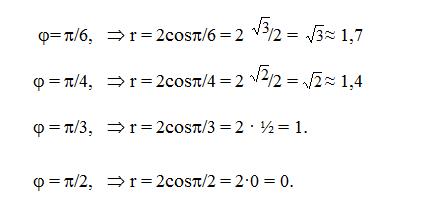
Если далее рассматривать углы из интервала (p/2; 3p/2), то значения r будут отрицательными, так как в этом промежутке cosj < 0. Это означает, что в области изменения j от p/2 до 3p/2 нет точек данной линии.
Если
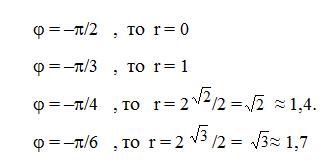
Запишем полученные данные в таблицу


Рис.1.7.12
Далее из полюса проводим лучи и откладываем на них соответствующие значения r. Соединяя полученные точки плавной линией, строим заданную кривую (рис.1.7.12).
Легко доказать, что построенная кривая является окружностью радиуса 1 с центром в точке (1, 0), лежащей на полярной оси. Действительно, выразив r и cosj из формул (1.6.2) и (1.6.3) и подставив их в уравнение кривой r = 2cosj, получим: x2 + y2 = 2x или (x – 1)2 + y2 = 1.
Пример. Построить линию, заданную уравнением x2 + y2 = 4y, перейдя в полярную систему координат.
Решение: Преобразуем данное уравнение, используя формулы (1.6.1)
x = rcos j, y = rsin j, получим: r2cos2j + r2sin2j = 4rsin j Þ
r2(cos2j + sin2j) = 4rsin j Þ r2 = 4rsin j Þ r = 4sin j.
Построим эту линию по точкам. Так как r ≥ 0, то 4sin j ≥ 0 Þ 0 ≤ j ≤ p .
Для вычисления значений r составляем таблицу:
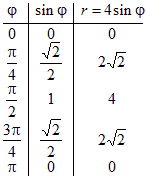
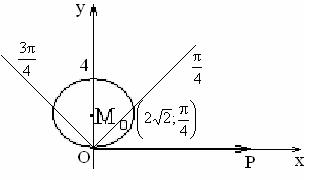
Рис.1.7.13
Далее из полюса проводим лучи и откладываем на них соответствующие значения r. Соединим полученные точки плавной линией. Построенная кривая (см. рис.1.7.13) является окружностью радиуса 2 с центром в точке M0(0, 2).
Матрицы и действия над ними. Основные операции над матрицами и их свойства
Матрицей размера m ´ n называется прямоугольная таблица чисел, состоящая из m строк и n столбцов:
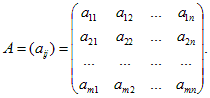
Числа aij называются элементами матрицы, первый индекс i означает номер строки, а второй индекс j – номер столбца, на пересечении которых находится элемент.
Если m = n, матрица называется квадратной, а число m = n – ее порядком.
Рассмотрим квадратную матрицу:

Говорят, что элементы a11, a22,… ann образуют главную диагональ, а элементы an1, an–1, 2,… a1n – побочную диагональ.
Верхней треугольной матрицей называется квадратная матрица, у которой все элементы, стоящие ниже главной диагонали, равны нулю:
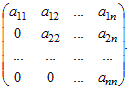
Нижней треугольной матрицей называется квадратная матрица, у которой все элементы, стоящие выше главной диагонали, равны нулю.
Диагональной матрицей называется квадратная матрица, у которой все элементы, не стоящие на главной диагонали, равны нулю:
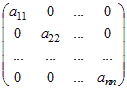
Диагональная матрица обозначается diag{a11, a22,… ann}.
Единичной матрицей называется диагональная матрица, у которой все диагональные элементы равны 1:

Нулевой матрицей называется матрица O, все элементы которой равны нулю.
Матрица, состоящая из одной строки, называется матрицей-строкой:
X = (x1 x2… xn).
Матрица, состоящая из одного столбца, называется матрицей-столбцом:
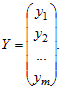
Две матрицы A = (aij) и B = (bij) одинакового размера m ´ n называются равными, если у них равны соответствующие элементы:
aij = bij при любых i = 1, 2,… m; j = 1, 2,… n.
Основные операции над матрицами и их свойства
Сложение матриц
Суммой двух матриц A = (aij) и B = (bij) одинакового размера m ´ n называется матрица C = A + B = (cij) того же размера, элементы которой равны сумме соответствующих элементов матриц A и B:
cij = aij + bij, при любых i = 1, 2,… m; j = 1, 2,… n.
Пример 1. Найти сумму двух матриц
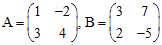
Решение. Складывая соответствующие элементы матриц, получаем:
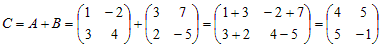
Умножение матрицы на число
Произведением матрицы A = (aij) размера m ´ n на число λ называется матрица С = λ·A = A·λ = (cij) того же размера, элементы которой равны соответствующим элементам матрицыA, умноженным на число λ:
cij = λ aij при любых i = 1, 2,… m; j = 1, 2,… n.
Пример 2. Найти произведение матрицы 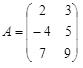 на число λ.
на число λ.
Решение. Умножив на λ каждый элемент матрицы A, получим
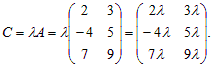
Вычитание матриц
Разностью двух матриц A и В одинакового размера m ´ n называется матрица
A–В=A+ (–1) В.
Матрица (–A) = (–1)A называется противоположной матрице A.
Дата: 2018-12-21, просмотров: 426.