В этом заключительном упражнении будте особенно осторожны, когда проверяете на делимость 7 и 17. Остальное должно быть лёгким для вас.


Обыкновенные дроби
Если вы в состоянии управиться с целыми числами, то арифмитические действия с дробями будет почти таким же лёгким. В этом разделе мы сделаем обзор основных методов сложения, вычитания, умножения, деления и упрощения обыкновенных дробей. Те, кто уже знаком с дробями, могут пропустить тот раздел без ущерба для целостности.
Перемножение обыкновенных дробей
Для перемножения двух обыкновенных дробей нуно просто перемножить верхние числа ( числители), а затем нижние (знаменатели). Например,

Что может быть легче! Попробуйте эти упражнения, прежде чем пойдёте дальше.
Упражнение: перемножение обыкновенных дробей
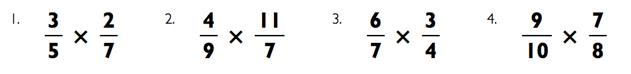
Деление обыкновенных дробей
Деление дробей такое же лёгкое, как и умножение. Тут только одно дополнительное действие. Сперва переверните левую дробь с ног на голову (это называется «обратная дробь»), а затем умножайте. Например, обратная дробь для 4/5 будет 5/4. Следовательно,
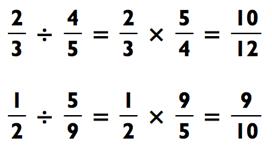
Упражнение: деление обыкновенных дробей
Теперь ваш черёд. Поделите эти дроби.
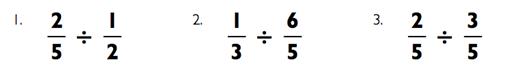
Упрощение обыкновенных дробей
Дроби можно рассматривать как маленькие задачки на деление. Например, 6/3 то же самое, что и 6/3 = 2. Дробь 1/4 то же самое, что и 1/4 (0,25 в десятичной форме). Теперь нам известно, что когда мы умножаем любое число на 1, то это число остаётся неизменным. Например, 3/5 = 3/5 х 1. Но если мы заменим 1 числом 2/2, то получим 3/5 = 3/5 х 1 = 3/5 х 2/2 = 6/10. Следовательно, 3/5 = 6/10. По такому же принципу, если мы заменим 1 числом 3/3, то получим 3/5 = 3/5 х 3/3 = 9/15. Другими словами, если мы умножаем числитель и знаменатель на одно и то же число, то получаем дробь равную исходной.
Вот другой пример,
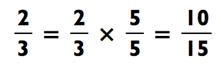
Верно и то, что если мы разделим числитель и знаменатель на одинаковое число, то получим дробь равную исходной.
Например,
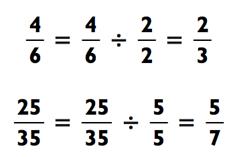
Это называется упрощение дроби.
Упражнение: упрощение дроби
Можете ли вы найти равную дробь со знаменателем 12 для дробей, представленных ниже?
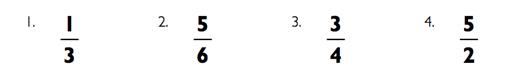
Упростите эти дроби.

Сложение дробей
Данное действие можно считать простым, когда знаменатели равны. Если это так, значит мы складываем числители и сохраняем прежний знаменатель.
Например,

Иногда мы можем упростить наш ответ. Например,
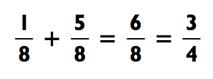
Упражнение: сложение дробей (равные знаменатели)

Более коварный случай - неравные знаменатели. Когда знаменатели отличаются, мы заменяем исходные дроби дробями с равными знаменателями.
Например, сложите
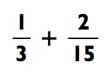
Мы заметели, что
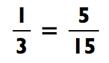
Следовательно,
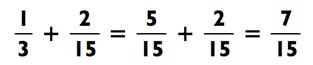
Во время сложения
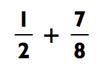
Мы заметили, что
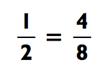
Таким образом,
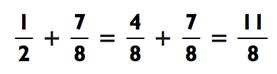
Во время сложения
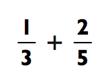
Мы увидели, что

В итоге,
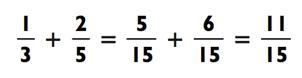
Дата: 2018-12-21, просмотров: 433.