Как вы могли догадаться, мне нравится делать ситуацию лучше, когда превращаю обычные дроби в десятичные. В случае с числом из одной цифры, лучший способ - доверить дроби (до 11 в знаминателе) памяти. Это не так сложно, как звучит. Как вы увидите ниже, большинство «одноцифровых» дробей обладают особыми качествами, из-за которых их сложно забыть. Каждый раз, когда вы сможете сократить дробь до уже известной вам, это ускорит процесс.

Шансы, что вы уже знаете десятичный эквивалент для следующих дробей:

Подобно этому:

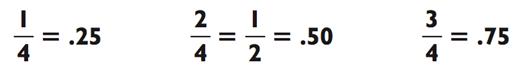
С пятёрками легче всего запомнить:

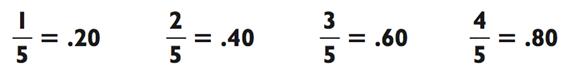
Шестёрки требуют запоминания только двух новых ответов:

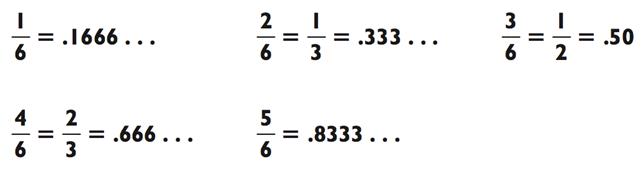
Через мгновенье я вернусь к семёркам. Восьмёрки - сплошные пустяки:

Девятки таят в себе своё собственное волшебство:

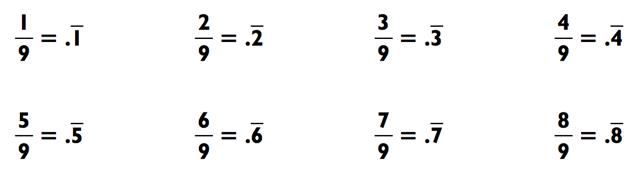
где чёрточка обозначает то, что дробь в периоде.

Например, 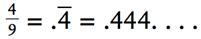                        Десятки нам уже известны:

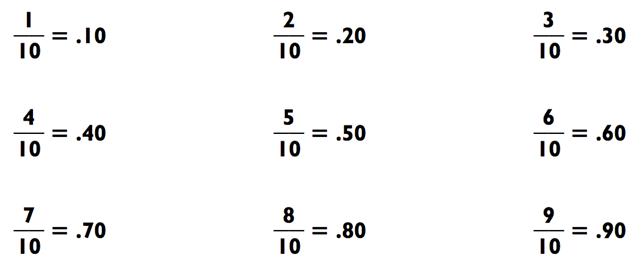
Для одиннадцати, если вы помните, что 1/11 = .0909, остальное будет лёгким:

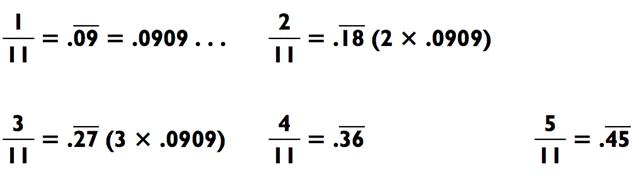
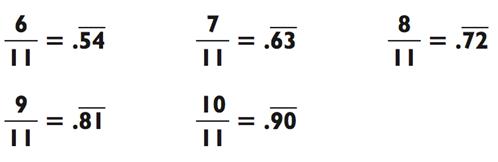
Семёрки действительно выдающиеся. Как только вы запомните

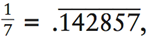
то сможете получить другие ответы без каких-либо вычислений:

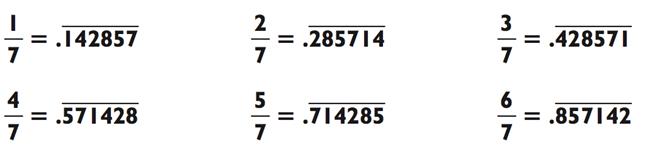
Обратите внимание, что цепочка цифр повторяется в каждой дроби. Изменяется лишь отправная точка. Вы можете определить её за мгновенье путём умножения 0,14 на числитель. В случае с 2/7, 2 х 0,14

= 0,28, так что используйте последовательность, которая начинается с

2. Так же и 3/7, раз 3 х 0,14 = 0,42, значит нужно использовать последовательность, начинающуюся с 4. Остальное поддаётся такому же правилу.

Вы будете вынуждены считать дроби больше, чем 10/11, когда столкнётесь с другими задачами. Однако, постоянно высматривайте способы упрощения таких задач. Например, вы можете упростить дробь 18/34 путём деления обоих чисел на 2, дабы сократить задачу до 9/17 (её будет легче решить).

Если знаменатель дроби - чётное число, то вы можете упростить дробь, сократив её вдвое, даже если числитель нечётный. Например:

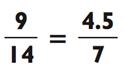
Деление числителя и знаменателя надвое сведёт проблему к дроби с семёркой. Хотя ранее показанная последовательность для такого случая и не предоставляет десятичного варианта для 4,5/7, как только вы начнёте считать, заученное число неожиданно всплывёт в памяти:

Как вы можете видеть, вам не пришлось решать задачу целиком. Как только вы сократили её, разделив 3 на 7, вы будете в состоянии произвести огромное впечатление на аудитории, отбарабанив этот длинный набор цифр почти мгновенно!

Когда делитель оканчивается на 5, то почти всегда удвоение задачки, а потом её разделение на 10 оправдывает себя. Например,

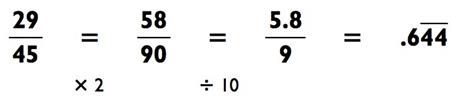
Числа, оканчивающиеся на 25 или 75 должны быть умножены на

4, прежде чем вы разделите их на 100.

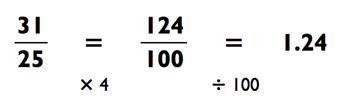
Вы даже можете ввести в использование этот трюк в середине решения. Если ваша дробь 3/16, смотрите, что произойдёт:

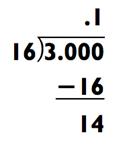
Как только задача сведётся к 14/16, далее вы можете привести её к виду 7/8, что, как вам известно, равняется 0,875. Отсюда 3/16 = 0,1875.